Problem

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Examples

Example 1:

1
2
3

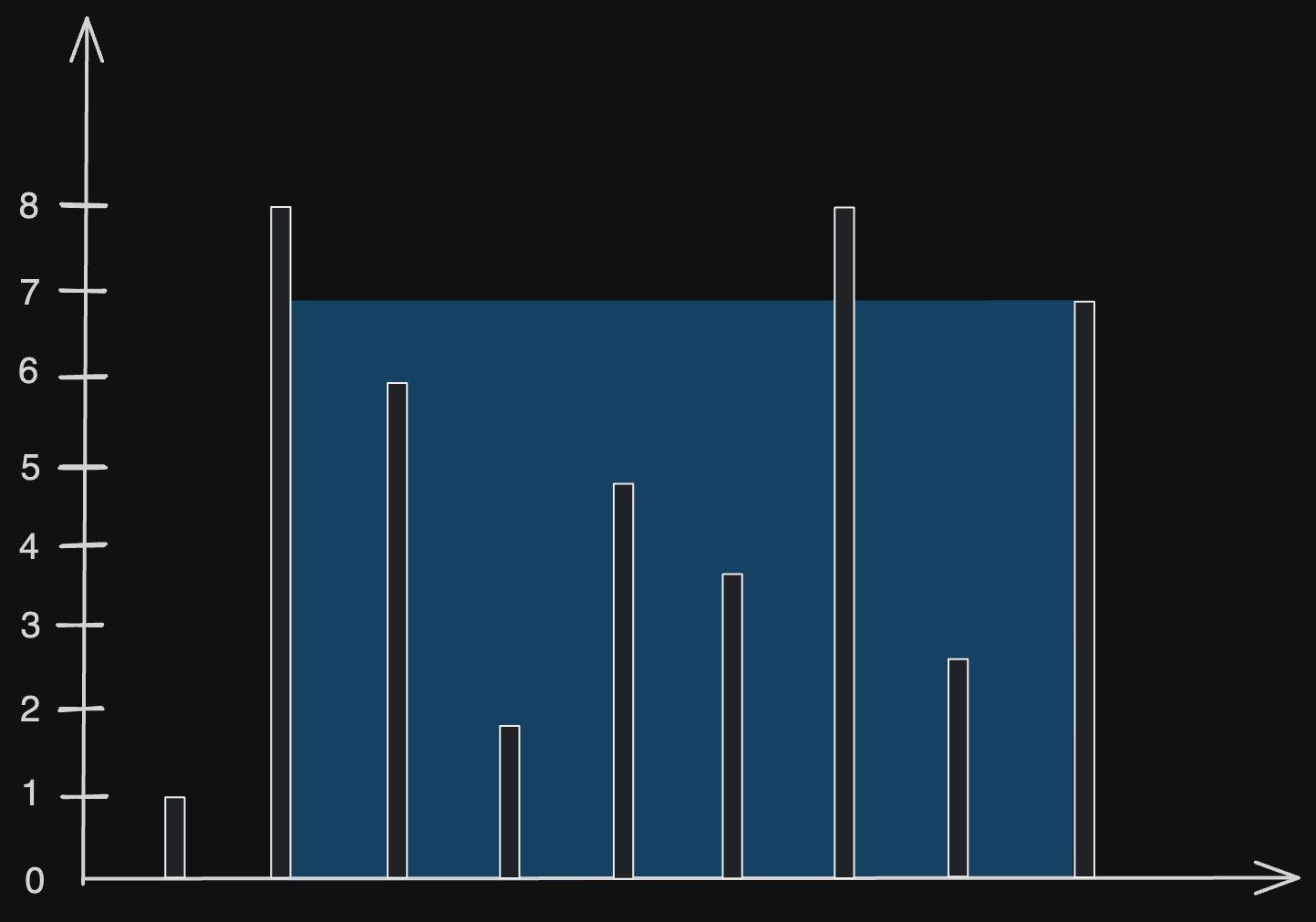
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

1
2
3
4

Input : [1, 5, 4, 3]
Output : 6
Explanation : 5 and 3 are distance 2 apart. So size of the base = 2. Height of container = min(5, 3) = 3.
So total area = 3 * 2 = 6

Solution

Video explanation

Here is the video explaining below methods in detail. Please check it out:

Method 1 - Naive

One straightforward method is to iterate through the height array, compute the potential volumes combining the current height with all other heights, and then identify the maximum value.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public int maxArea(int[] height) {
        int maxArea = 0;
        int n = height.length;
        
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                // Calculate the area for each pair (i, j)
                int area = Math.min(height[i], height[j]) * (j - i);
                maxArea = Math.max(maxArea, area);
            }
        }
        
        return maxArea;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area: int = 0
        n: int = len(height)
        
        for i in range(n):
            for j in range(i + 1, n):
                # Calculate the area for each pair (i, j)
                area = min(height[i], height[j]) * (j - i)
                max_area = max(max_area, area)
        
        return max_area

Complexity

  • ⏰ Time complexity: O(n^2)
  • 🧺 Space complexity: O(1)

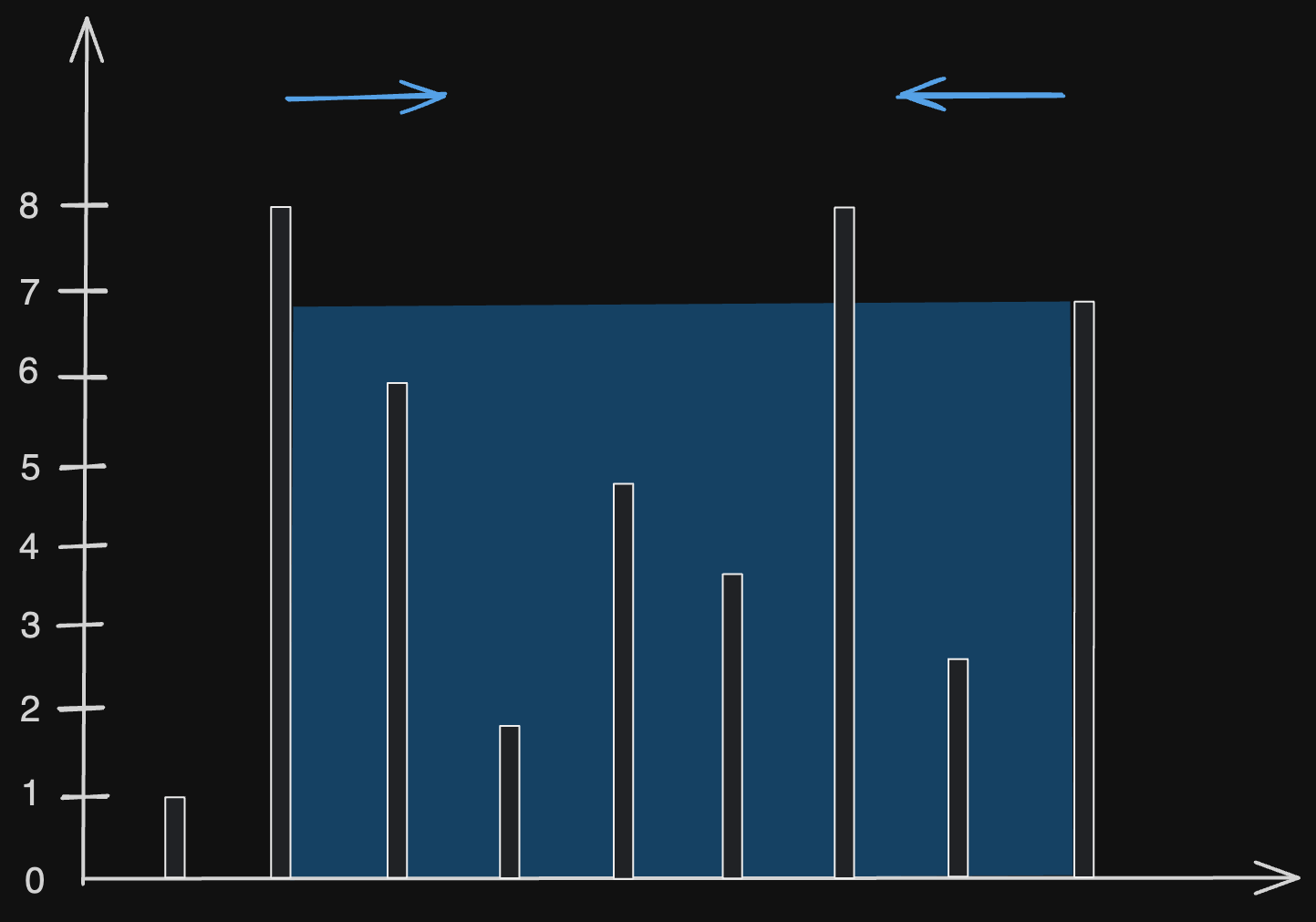
Method 2 - Using Two Pointers

The volume of a container is determined by two factors: width and height. By starting from both ends of the array and moving towards the middle, height becomes the limiting factor.

Initially, assume the result is 0 and scan the array from both ends. If the left height is less than the right height, move the left pointer rightwards to find a higher value. Conversely, if the left height is greater than the right height, move the right pointer leftwards to find a higher value. Throughout the process, continually track the maximum value.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    public int maxArea(int[] height) {
        int l = 0, r = height.length - 1;
        int ans = 0;
        
        while (l < r) {
            // Calculate area and update max
            int area = Math.min(height[l], height[r]) * (r - l);
            ans = Math.max(ans, area);
            
            // Move the pointer associated with smaller height
            if (height[l] < height[r]) {
                l++;
            } else {
                r--;
            }
        }
        
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l, r = 0, len(height) - 1
        ans: int = 0
        
        while l < r:
            # Calculate area and update max
            area = min(height[l], height[r]) * (r - l)
            ans = max(ans, area)
            
            # Move the pointer associated with smaller height
            if height[l] < height[r]:
                l += 1
            else:
                r -= 1
        
        return ans

Complexity

  • ⏰ Time complexity: O(n)
  • 🧺 Space complexity: O(1)