Problem

Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.

Examples

Example 1: 

1
2

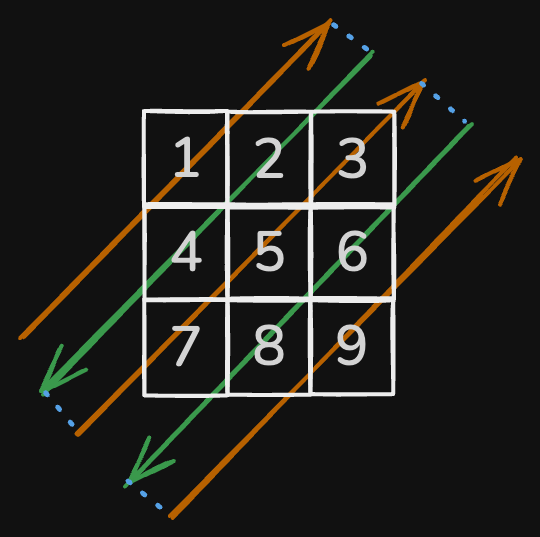
Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Example 2:

1
2

Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]

Solution

Method 1 - Iteration with change in direction

Here is the approach:

  1. Matrix Traversal:
    • Traverse the matrix starting from mat[0][0] and moving in a diagonal fashion.
    • Alternately change the direction of traversal from upward to downward and vice versa.
  2. Boundary Conditions:
    • Adjust the coordinates when reaching the matrix boundaries to ensure the traversal stays within bounds.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

public class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        if (mat == null || mat.length == 0) return new int[0];
        
        int m = mat.length;
        int n = mat[0].length;
        int[] result = new int[m * n];
        
        int row = 0, col = 0;
        int direction = 1;  // 1 means up, -1 means down
        for (int i = 0; i < m * n; i++) {
            result[i] = mat[row][col];
            if (direction == 1) {  // Moving up
                if (col == n - 1) { 
                    row++;
                    direction = -1;
                } else if (row == 0) { 
                    col++;
                    direction = -1;
                } else {
                    row--;
                    col++;
                }
            } else {  // Moving down
                if (row == m - 1) { 
                    col++;
                    direction = 1;
                } else if (col == 0) { 
                    row++;
                    direction = 1;
                } else {
                    row++;
                    col--;
                }
            }
        }
        
        return result;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        if not mat or not mat[0]:
            return []
            
        m, n = len(mat), len(mat[0])
        result = []
        
        row, col = 0, 0
        direction = 1  # 1 means up, -1 means down
        for _ in range(m * n):
            result.append(mat[row][col])
            if direction == 1:  # Moving up
                if col == n - 1:
                    row += 1
                    direction = -1
                elif row == 0:
                    col += 1
                    direction = -1
                else:
                    row -= 1
                    col += 1
            else:  # Moving down
                if row == m - 1:
                    col += 1
                    direction = 1
                elif col == 0:
                    row += 1
                    direction = 1
                else:
                    row += 1
                    col -= 1
        
        return result

Complexity

  • ⏰ Time complexity: O(m * n), where m is the number of rows and n is the number of columns, because we visit each cell exactly once.
  • 🧺 Space complexity: O(1), ignoring the space used for the output array.