Generate Nth Fibonacci Number

Problem

The [Fibonacci Numbers](fibonacci-numbers), commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

Sequence is defined as, $F_{0} = 0$ and $F_{1} = 1$ and $F_{n} = F_{n-1} + F_{n-2}$

Given n, calculate F(n).

Examples

Example 1:

Input : n = 2
Output : 1

Example 2:

Input : n = 9
Output : 34

Solution

Video explanation

Here is the video explaining this method in detail. Please check it out:

Method 1 - Use Recursion

A simple method that is a direct recursive implementation mathematical recurrence relation given above.

Code

Java

class Solution {

    // Method to calculate the Fibonacci number for a given input `n`
    public int fib(int n) {
        // Base case 1: If `n` is 0, return 0 as `F(0) = 0`
        if (n == 0) return 0;

        // Base case 2: If `n` is 1, return 1 as `F(1) = 1`
        if (n == 1) return 1;

        // Recursive call: `F(n) = F(n-1) + F(n-2)`
        return fib(n - 1) + fib(n - 2);
    }
}

Python

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        return self.fib(n - 1) + self.fib(n - 2)

Time Complexity

Time Complexity: T(n) = T(n-1) + T(n-2) = O(2^n) which is exponential.
Space complexity: O(1) (assuming recursive stack is okay)

Method 2 - Top Down DP

We can observe that this implementation does a lot of repeated work (see the following recursion tree below, where F(3) and F(2) is calculated twice). So this is a bad implementation for nth Fibonacci number.

Recursion tree for execution of fib(5):

 graph TD
     F5["F(5)"]
     F5 --> F4["F(4)"]:::blue
     F5 --> F3["F(3)"]:::green
     F4 --> F3_1["F(3)"]:::green
     F4 --> F2["F(2)"]:::orange
     F3 --> F2_1["F(2)"]:::orange
     F3 --> F1["F(1)"]:::red
     F3_1 --> F2_2["F(2)"]:::orange
     F3_1 --> F1_1["F(1)"]:::red
     F2 --> F1_2["F(1)"]:::red
     F2 --> F0["F(0)"]:::purple
     F2_1 --> F1_3["F(1)"]:::red
     F2_1 --> F0_1["F(0)"]:::purple
     F2_2 --> F1_4["F(1)"]:::red
     F2_2 --> F0_2["F(0)"]:::purple
 
     %% Styles for coloring duplicate nodes %%
     classDef unique fill:#f9f,stroke:#333,stroke-width:2px;
     classDef blue fill:#87CEEB,stroke:#333,stroke-width:2px;
     classDef green fill:#90EE90,stroke:#333,stroke-width:2px;
     classDef orange fill:#FFA07A,stroke:#333,stroke-width:2px;
     classDef red fill:#FFC0CB,stroke:#333,stroke-width:2px;
     classDef purple fill:#DDA0DD,stroke:#333,stroke-width:2px;

If you prefer slightly cleaner image:

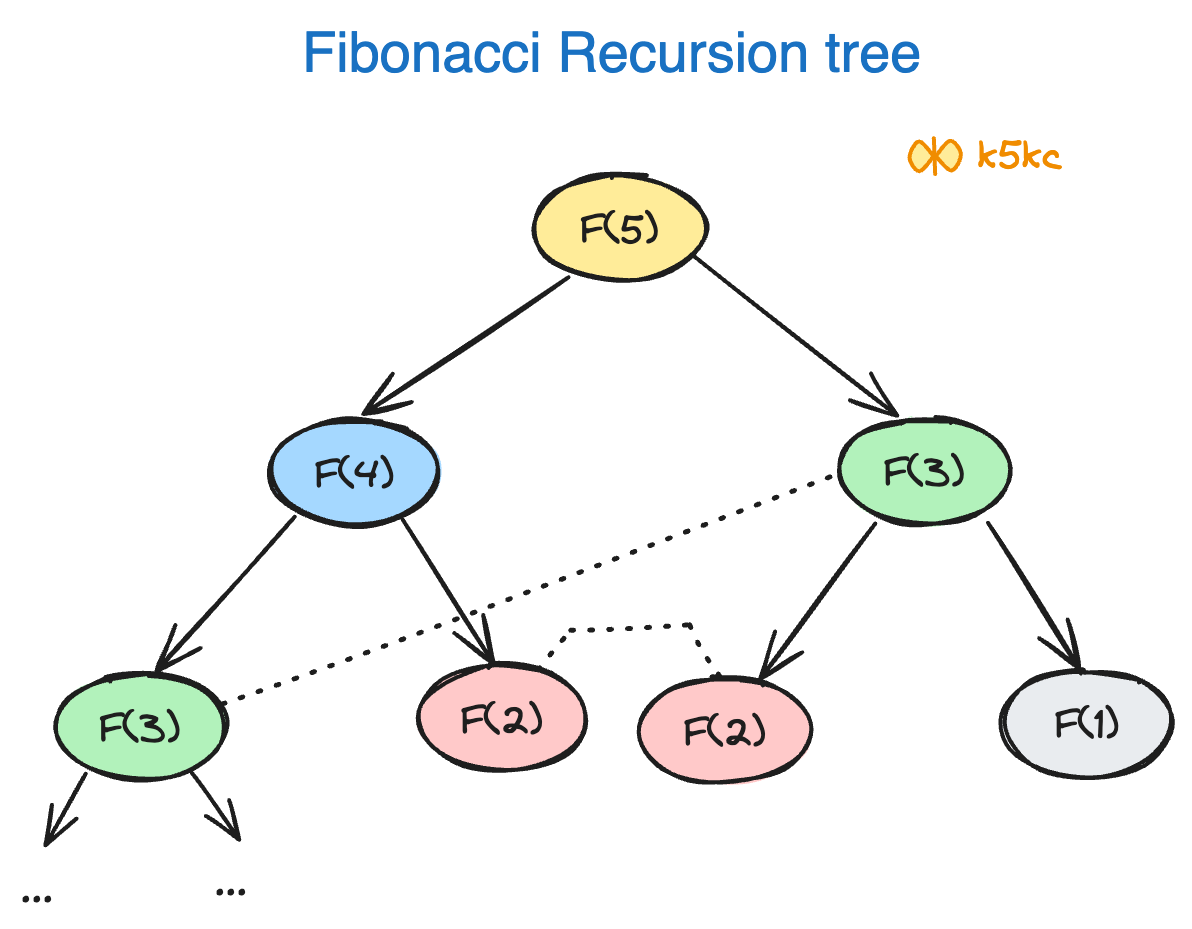
As we saw above, this problem shows the overlapping subproblems pattern, so let’s make use of memoization here. We can use an array to store the already solved subproblems (see the changes in the highlighted lines).

Code

Java

class Solution {

    public int fib(int n) {
        // If n is 0, directly return 0 (base case)
        if (n == 0) return 0;

        // Create an array for memoisation
        int[] memo = new int[n + 1];

        // Initialise base cases
        memo[0] = 0;
        memo[1] = 1;

        // Call the helper function to compute Fibonacci recursively
        return helper(n, memo);
    }

    private int helper(int n, int[] memo) {
        // If already computed, return the cached result
        if (memo[n] != 0 || n == 1) return memo[n];

        // Otherwise, compute and store it
        memo[n] = helper(n - 1, memo) + helper(n - 2, memo);

        return memo[n];
    }
}

C++


std::function<int(int)> f = [&] (int x) { return (x < 2) ? x : f(x-1) +
f(x-2); };

Optimized Version:

std::vector<int> cache = {0, 1};
    
     std::function<int(int)> f = [&] (int x)
     {
         if (cache.size() > x) return cache[x];
        
         cache.push_back(f(x-1) + f(x-2));
        
         return cache.back();

    };

Python

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0

        # Create a list for memoisation
        memo = [0] * (n + 1)

        # Initialise base cases
        memo[0] = 0
        memo[1] = 1

        # Define the helper function
        def helper(n: int) -> int:
            if memo[n] != 0 or n == 1:
                return memo[n]

            # Compute and cache the value
            memo[n] = helper(n - 1) + helper(n - 2)
            return memo[n]

        return helper(n)

Complexity

⏰ Time complexity: O(n)
🧺 Space complexity: O(n)

Method 3 - Bottom Up DP

Let’s apply Tabulation to our example of Fibonacci numbers. Since we know that every Fibonacci number is the sum of the two preceding numbers, we can use this fact to populate our table.

Code

Java

class Solution {

    public int fib(int n) {
        // Handle base cases directly
        if (n == 0) return 0;
        if (n == 1) return 1;

        // Create an array to store Fibonacci numbers
        int[] dp = new int[n + 1];

        // Initialise base cases
        dp[0] = 0;
        dp[1] = 1;

        // Fill the array in a bottom-up manner
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        // Return the nth Fibonacci number
        return dp[n];
    }
}

Python

class Solution:
    def fib(self, n: int) -> int:
        # Handle base cases directly
        if n == 0:
            return 0
        if n == 1:
            return 1

        # Create a list to store Fibonacci numbers
        dp = [0] * (n + 1)

        # Initialise base cases
        dp[0] = 0
        dp[1] = 1

        # Fill the list in a bottom-up manner
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]

        # Return the nth Fibonacci number
        return dp[n]

Complexity

⏰ Time complexity: O(n), as the loop runs from 2 to n, so the time complexity is O(n).
🧺 Space complexity: O(n)as the array (or list) of size n + 1 is used to store intermediate Fibonacci values, so the space complexity is O(n).

Method 4 - Space Optimized DP

We can optimize the space used in method 2 by storing the previous two numbers only because that is all we need to get the next Fibonacci number in series.

Code

Java

class Solution {

    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;

        int prev1 = 0, prev2 = 1, ans = 0;
        for (int i = 2; i <= n; i++) {
            ans = prev1 + prev2;
            prev1 = prev2;
            prev2 = ans;
        }
        return ans;
    }
}

Python

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        
        prev1: int = 0
        prev2: int = 1
        ans: int = 0
        
        for _ in range(2, n + 1):
            ans = prev1 + prev2
            prev1 = prev2
            prev2 = ans
        
        return ans

Complexity

⏰ Time complexity: O(n) due to sequential calculations
🧺 Space complexity: O(1) as we use only 2 variables.

Method 5 - Using power of the matrix

The Fibonacci sequence can be expressed using the following matrix recurrence relation:

\begin{bmatrix} F(n+1) & F(n) \\\ F(n) & F(n-1) \end{bmatrix} = \begin{bmatrix} 1 & 1 \\\ 1 & 0 \end{bmatrix} ^n

In simpler terms, the nth Fibonacci number is found in the top-left entry of:

\text{Matrix} = \begin{bmatrix} 1 & 1 \\\ 1 & 0 \end{bmatrix} ^n

Thus, calculating Fibonacci numbers reduces to raising a 2x2 matrix to the power ( n ).

Steps

1. Base Case:

- For ( n = 0 ) ⇨ `F(0) = 0`
- For ( n = 1 ) ⇨ `F(1) = 1`

2. Matrix Representation of the Recurrence Relation:

M = \begin{bmatrix} 1 & 1 \\\ 1 & 0 \end{bmatrix}

and set the initial result matrix ( R ) to the identity matrix:

I = \begin{bmatrix} 1 & 0 \\\ 0 & 1 \end{bmatrix}

3. Exponentiation with Binary Exponentiation:

Use matrix exponentiation (through binary exponentiation) to raise ( M ) to the power ( n-1 ):

If n is even, split the exponentiation into smaller powers:

M^n = (M^{n/2}) \cdot (M^{n/2})

if n is odd:

M^n = M \cdot M^{n-1}

4. Extract the Fibonacci Number: After computing ( M^{n-1} ), the Fibonacci number ( F(n) ) is located at the top-left (0, 0) entry of the resulting matrix.

Code

Java

class Solution {

    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;

        // Base matrix for Fibonacci
        int[][] baseMatrix = { { 1, 1 }, { 1, 0 } };

        // Exponentiate the matrix to (n - 1)
        int[][] resultMatrix = matrixExponentiation(baseMatrix, n - 1);

        // Return the top-left element as the Fibonacci number
        return resultMatrix[0][0];
    }

    // Helper function to perform matrix multiplication
    private int[][] multiplyMatrices(int[][] a, int[][] b) {
        return new int[][] {
            {
                a[0][0] * b[0][0] + a[0][1] * b[1][0],
                a[0][0] * b[0][1] + a[0][1] * b[1][1],
            },
            {
                a[1][0] * b[0][0] + a[1][1] * b[1][0],
                a[1][0] * b[0][1] + a[1][1] * b[1][1],
            },
        };
    }

    // Helper function to perform matrix exponentiation
    private int[][] matrixExponentiation(int[][] matrix, int power) {
        // Identity matrix
        int[][] result = { { 1, 0 }, { 0, 1 } };

        while (power > 0) {
            if (power % 2 == 1) {
                result = multiplyMatrices(result, matrix); // Odd power
            }
            matrix = multiplyMatrices(matrix, matrix); // Square the matrix
            power /= 2;
        }

        return result;
    }
}

Python

class Solution:
    def fib(self, n: int) -> int:
        if n == 0: return 0
        if n == 1: return 1
        
        # Function to multiply two 2x2 matrices
        def multiply_matrices(a, b):
            return [
                [a[0][0] * b[0][0] + a[0][1] * b[1][0], a[0][0] * b[0][1] + a[0][1] * b[1][1]],
                [a[1][0] * b[0][0] + a[1][1] * b[1][0], a[1][0] * b[0][1] + a[1][1] * b[1][1]],
            ]

        # Function to exponentiate the matrix using binary exponentiation
        def matrix_exponentiation(matrix, power):
            # Identity matrix
            result = [[1, 0], [0, 1]]
            while power > 0:
                if power % 2:  # If power is odd
                    result = multiply_matrices(result, matrix)
                matrix = multiply_matrices(matrix, matrix)
                power //= 2
            return result

        # Base Fibonacci matrix
        base_matrix = [[1, 1], [1, 0]]
        result_matrix = matrix_exponentiation(base_matrix, n - 1)
        return result_matrix[0][0]

Complexity

⏰ Time complexity: O(log n) for matrix exponentiation.
🧺 Space complexity: O(1) as we just use extra memory 2x2 matrix, which is constant.

Method 6 - Using Binet's Formula

Can there be formula for Fibonacci numbers in terms of n? Answer is yes.

The formula is called Binet’s formula. It uses something called golden ratio.

Golden Ratio (φ)

An irrational number approximately equal to 1.6180339887...
Can be expressed mathematically as: φ = (1 + √5) / 2

Binet’s Formula

F(n) = \frac{\phi ^ n - \phi ^ {-n}}{\sqrt{5}}

Limitations

However, this formula has limitations:

It involves powers of φ, which is an irrational number. Calculating exact values with an irrational number can be complex, especially for larger n.
The square root of 5 (√5) is another irrational number, adding further complexity.

Therefore, Binet's formula is not typically used for practical calculations of Fibonacci numbers due to its reliance on irrational numbers.

Complexity

⏰ Time complexity: O(1)
🧺 Space complexity: O(1)

Problem

Examples

Solution

Video explanation

Method 1 - Use Recursion

Code

Java

Python

Time Complexity

Method 2 - Top Down DP

Code

Java

C++

Python

Complexity

Method 3 - Bottom Up DP

Code

Java

Python

Complexity

Method 4 - Space Optimized DP

Code

Java

Python

Complexity

Method 5 - Using power of the matrix

Steps

Code

Java

Python

Complexity

Method 6 - Using Binet's Formula

Golden Ratio (φ)

Binet’s Formula

Limitations

Complexity

Comments