Maximum Number of Events That Can Be Attended

Problem

You are given an array of events where events[i] = [startDayi, endDayi]. Every event i starts at startDayi and ends at endDayi.

You can attend an event i at any day d where startTimei <= d <= endTimei. You can only attend one event at any time d.

Return the maximum number of events you can attend.

Examples

Example 1:

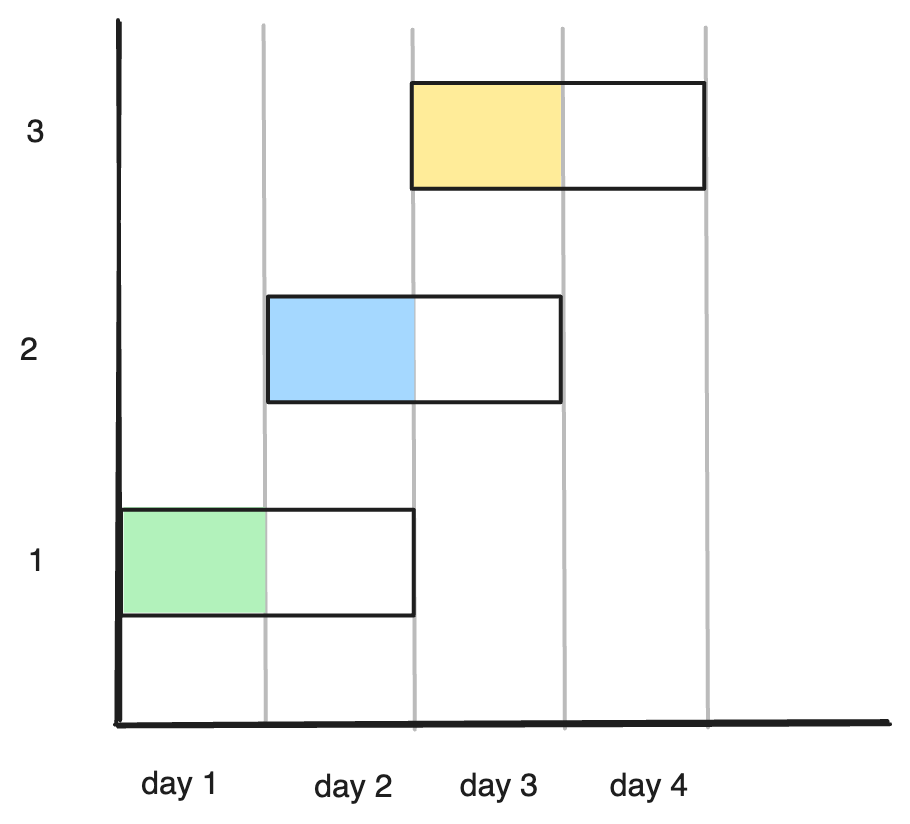
Input: events =[[1,2],[2,3],[3,4]]
Output: 3
Explanation: You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.

Example 2:

Input: events=[[1,2],[2,3],[3,4],[1,2]]
Output: 4

Constraints:

• 1 <= events.length <= 105
• events[i].length == 2
• 1 <= startDayi <= endDayi <= 105

Solution

Method 1 – Greedy with Min Heap

Intuition

To maximize the number of events attended, always attend the event that ends earliest among all available events for each day. By using a min-heap to track the end days of available events, we can efficiently pick the next event to attend and skip days/events that are no longer possible.

Approach

1. Sort the events by their start day.
2. Initialize a min-heap to keep track of end days of events that can be attended on the current day.
3. For each day from the earliest start to the latest end:
   • Add all events starting on this day to the heap.
   • Remove events from the heap that have already ended.
   • If the heap is not empty, attend the event with the earliest end day (pop from heap), and increment the answer.
4. Continue until all events are processed.
5. Return the total number of events attended.

Code

C++

class Solution {
public:
    int maxEvents(vector<vector<int>>& events) {
        sort(events.begin(), events.end());
        priority_queue<int, vector<int>, greater<int>> pq;
        int i = 0, n = events.size(), ans = 0;
        int day = 1;
        while (i < n || !pq.empty()) {
            if (pq.empty() && day < events[i][0]) day = events[i][0];
            while (i < n && events[i][0] == day) pq.push(events[i++][1]);
            while (!pq.empty() && pq.top() < day) pq.pop();
            if (!pq.empty()) {
                pq.pop();
                ans++;
            }
            day++;
        }
        return ans;
    }
};

Go

import "container/heap"
func maxEvents(events [][]int) int {
    sort.Slice(events, func(i, j int) bool { return events[i][0] < events[j][0] })
    h := &IntHeap{}
    i, n, ans, day := 0, len(events), 0, 1
    for i < n || h.Len() > 0 {
        if h.Len() == 0 && day < events[i][0] {
            day = events[i][0]
        }
        for i < n && events[i][0] == day {
            heap.Push(h, events[i][1])
            i++
        }
        for h.Len() > 0 && (*h)[0] < day {
            heap.Pop(h)
        }
        if h.Len() > 0 {
            heap.Pop(h)
            ans++
        }
        day++
    }
    return ans
}
// IntHeap implements heap.Interface for []int (min-heap)
type IntHeap []int
func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *IntHeap) Push(x interface{}) { *h = append(*h, x.(int)) }
func (h *IntHeap) Pop() interface{} {
    old := *h
    x := old[len(old)-1]
    *h = old[:len(old)-1]
    return x
}

Java

class Solution {
    public int maxEvents(int[][] events) {
        Arrays.sort(events, (a, b) -> a[0] - b[0]);
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        int i = 0, n = events.length, ans = 0, day = 1;
        while (i < n || !pq.isEmpty()) {
            if (pq.isEmpty() && day < events[i][0]) day = events[i][0];
            while (i < n && events[i][0] == day) pq.offer(events[i++][1]);
            while (!pq.isEmpty() && pq.peek() < day) pq.poll();
            if (!pq.isEmpty()) {
                pq.poll();
                ans++;
            }
            day++;
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun maxEvents(events: Array<IntArray>): Int {
        events.sortBy { it[0] }
        val pq = java.util.PriorityQueue<Int>()
        var i = 0
        var ans = 0
        var day = 1
        while (i < events.size || pq.isNotEmpty()) {
            if (pq.isEmpty() && day < events[i][0]) day = events[i][0]
            while (i < events.size && events[i][0] == day) pq.add(events[i++][1])
            while (pq.isNotEmpty() && pq.peek() < day) pq.poll()
            if (pq.isNotEmpty()) {
                pq.poll()
                ans++
            }
            day++
        }
        return ans
    }
}

Python

class Solution:
    def maxEvents(self, events: list[list[int]]) -> int:
        import heapq
        events.sort()
        pq = []
        i = ans = 0
        n = len(events)
        day = 1
        while i < n or pq:
            if not pq and day < events[i][0]:
                day = events[i][0]
            while i < n and events[i][0] == day:
                heapq.heappush(pq, events[i][1])
                i += 1
            while pq and pq[0] < day:
                heapq.heappop(pq)
            if pq:
                heapq.heappop(pq)
                ans += 1
            day += 1
        return ans

Rust

impl Solution {
    pub fn max_events(mut events: Vec<Vec<i32>>) -> i32 {
        use std::collections::BinaryHeap;
        events.sort();
        let mut pq = std::collections::BinaryHeap::new();
        let mut i = 0;
        let n = events.len();
        let mut ans = 0;
        let mut day = 1;
        while i < n || !pq.is_empty() {
            if pq.is_empty() && day < events[i][0] { day = events[i][0]; }
            while i < n && events[i][0] == day {
                pq.push(-events[i][1]);
                i += 1;
            }
            while !pq.is_empty() && -pq.peek().unwrap() < day {
                pq.pop();
            }
            if !pq.is_empty() {
                pq.pop();
                ans += 1;
            }
            day += 1;
        }
        ans
    }
}

TypeScript

class Solution {
    maxEvents(events: number[][]): number {
        events.sort((a, b) => a[0] - b[0]);
        const pq: number[] = [];
        let i = 0, ans = 0, day = 1;
        while (i < events.length || pq.length) {
            if (!pq.length && day < events[i][0]) day = events[i][0];
            while (i < events.length && events[i][0] === day) pq.push(events[i++][1]);
            pq.sort((a, b) => a - b);
            while (pq.length && pq[0] < day) pq.shift();
            if (pq.length) {
                pq.shift();
                ans++;
            }
            day++;
        }
        return ans;
    }
}

Method 2 – Segment Tree (Range Query)

Intuition

We can use a segment tree to efficiently find the earliest available day to attend an event in its interval. For each event, we query the segment tree for the minimum available day in its range, and if found, mark that day as used. This allows us to maximize the number of events attended.

Approach

1. Sort events by their end day (to prioritize earliest finishing events).
2. Build a segment tree to track available days (1 for available, 0 for used) in the range [1, max end day].
3. For each event, query the segment tree for the minimum available day in [start, end].
4. If a day is found, mark it as used in the segment tree and increment the answer.
5. Return the total number of events attended.

Code

C++

class SegmentTree {
    vector<int> tree;
    int n;
public:
    SegmentTree(int n): n(n), tree(4 * n, 1) {}
    int query(int l, int r, int s, int e, int idx) {
        if (l > e || r < s) return -1;
        if (tree[idx] == 0) return -1;
        if (s == e) return s;
        int m = (s + e) / 2;
        int left = query(l, r, s, m, 2 * idx);
        if (left != -1) return left;
        return query(l, r, m + 1, e, 2 * idx + 1);
    }
    void update(int pos, int s, int e, int idx) {
        if (s == e) { tree[idx] = 0; return; }
        int m = (s + e) / 2;
        if (pos <= m) update(pos, s, m, 2 * idx);
        else update(pos, m + 1, e, 2 * idx + 1);
        tree[idx] = tree[2 * idx] | tree[2 * idx + 1];
    }
};
class Solution {
public:
    int maxEvents(vector<vector<int>>& events) {
        int maxd = 0;
        for (auto& e : events) maxd = max(maxd, e[1]);
        sort(events.begin(), events.end(), [](auto& a, auto& b) { return a[1] < b[1]; });
        SegmentTree st(maxd + 2);
        int ans = 0;
        for (auto& e : events) {
            int d = st.query(e[0], e[1], 1, maxd, 1);
            if (d != -1) {
                st.update(d, 1, maxd, 1);
                ans++;
            }
        }
        return ans;
    }
};

Python

class SegmentTree:
    def __init__(self, n):
        self.n = n
        self.tree = [1] * (4 * n)
    def query(self, l, r, s, e, idx):
        if l > e or r < s:
            return -1
        if self.tree[idx] == 0:
            return -1
        if s == e:
            return s
        m = (s + e) // 2
        left = self.query(l, r, s, m, 2 * idx)
        if left != -1:
            return left
        return self.query(l, r, m + 1, e, 2 * idx + 1)
    def update(self, pos, s, e, idx):
        if s == e:
            self.tree[idx] = 0
            return
        m = (s + e) // 2
        if pos <= m:
            self.update(pos, s, m, 2 * idx)
        else:
            self.update(pos, m + 1, e, 2 * idx + 1)
        self.tree[idx] = self.tree[2 * idx] | self.tree[2 * idx + 1]
class Solution:
    def maxEvents(self, events: list[list[int]]) -> int:
        maxd = max(e[1] for e in events)
        events.sort(key=lambda x: x[1])
        st = SegmentTree(maxd + 2)
        ans = 0
        for s, e in events:
            d = st.query(s, e, 1, maxd, 1)
            if d != -1:
                st.update(d, 1, maxd, 1)
                ans += 1
        return ans

Complexity

• ⏰ Time complexity: O(n log D), where n is the number of events and D is the range of days. Each query/update is O(log D).
• 🧺 Space complexity: O(D), for the segment tree.