Problem

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m-1][n-1]). The robot can only move in any four directions(up, down, right, left) at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return all possible unique paths that the robot can take to reach the bottom-right corner.

This problem is similar to Unique Paths in Grid - Get all paths moving right or down with obstacles but robot can move in all 4 directions.

Examples

Example 1:

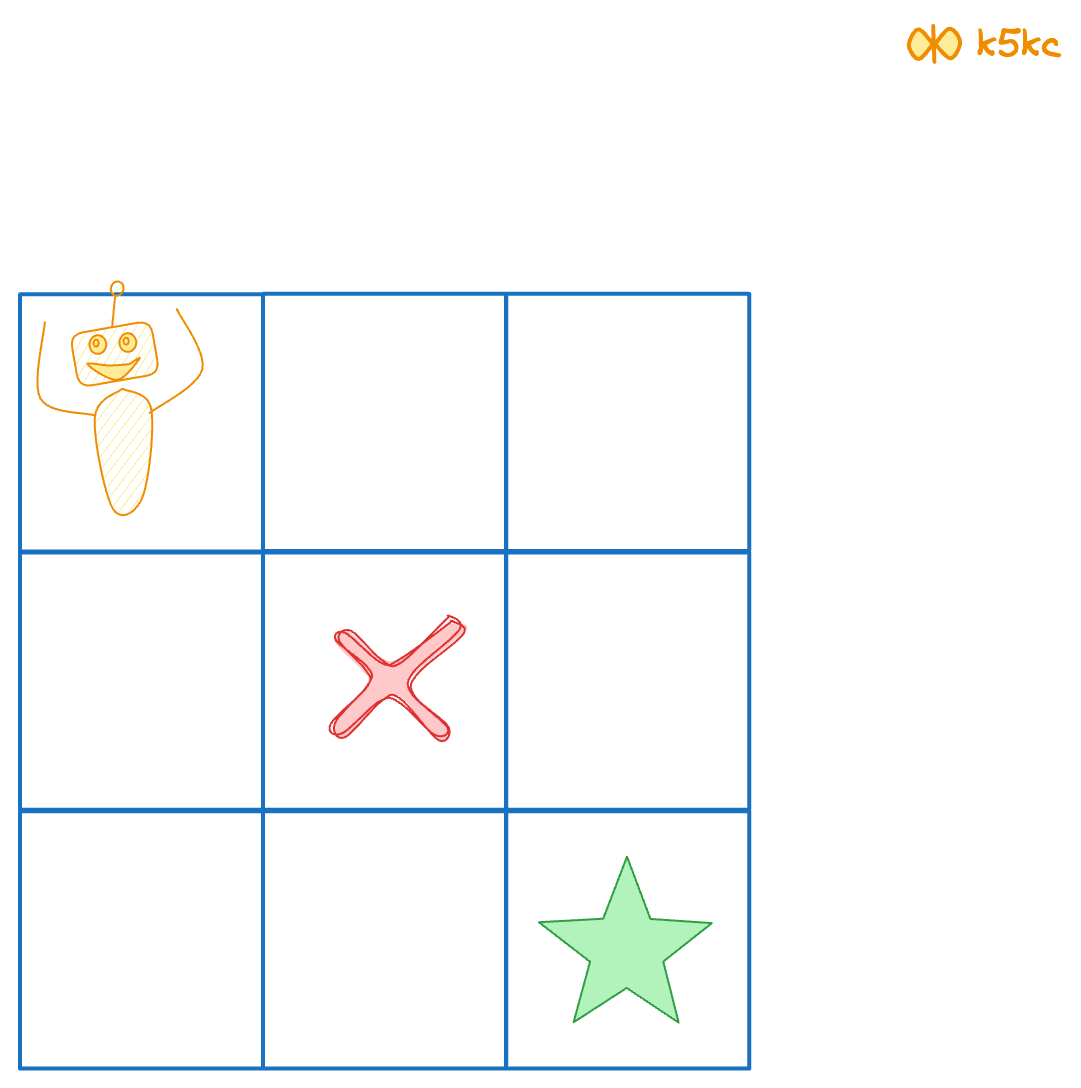
There is one obstacle in the middle of a 3x3 grid as illustrated below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

Input:
obstacleGrid =[[0,0,0],[0,1,0],[0,0,0]]
Output:
 [ 
	[[0, 0], [0, 1], [0, 2], [1, 2], [2, 2]],
	[[0, 0], [1, 0], [2, 0], [2, 1], [2, 2]]
 ]
 
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Example 2:

1
2
3
4
5
6

Input:
obstacleGrid =[[0,1],[0,0]]
Output:
 [ 
	[[0, 0], [1, 0], [1, 1]]
 ]

Solution

Naive Algorithm The Naive Algorithm is to generate all paths from source to destination and one by one check if the generated path satisfies the constraints.

1
2
3
4
5
6

while there are untried paths {
       generate the next path
       if this path has all blocks as 1 {
              print this path;
       }
}

Method 1 - Backtracking Algorithm

  • We initialize result to an empty list that will eventually contain all unique valid paths.
  • We check if the starting or ending cell is an obstacle. If so, we immediately return the empty list.
  • We use a visited boolean array to make sure that we do not include any cell more than once in the same path.
  • The backtrack method explores all four directions recursively. After exploring, we undo the step (backtrack) so we can explore different paths.
  • When we reach the bottom-right corner of the grid, we add the current path to our result list.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

public class Solution {

	public List <List<int[] >> uniquePathsWithObstacles(int[][] grid) {
		List <List<int[] >> ans = new ArrayList<>();
		int m = grid.length;
		int n = grid[0].length;
		if (grid[0][0] == 1 || grid[m - 1][n - 1] == 1) {
			return ans; // Cannot start or end on an obstacle.
		}

		boolean[][] visited = new boolean[m][n];
		backtrack(0, 0, grid, visited, new ArrayList<>(), ans);
		return ans;
	}

	private void backtrack(int row, int col, int[][] grid, boolean[][] visited, List<int[]> path, List <List<int[]>> result) {
		// Check for invalid conditions
		if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length ||
			grid[row][col] == 1 || visited[row][col]) {
			return;
		}

		// Add to path
		path.add(new int[] {
			row, col
		});
		visited[row][col] = true;

		// Check if we've reached the destination
		if (row == grid.length - 1 && col == grid[0].length - 1) {
			result.add(new ArrayList<>(path));
		} else {
			// Explore all four directions
			backtrack(row + 1, col, grid, visited, path, result); // Down
			backtrack(row - 1, col, grid, visited, path, result); // Up
			backtrack(row, col + 1, grid, visited, path, result); // Right
			backtrack(row, col - 1, grid, visited, path, result); // Left
		}

		// Remove from path and mark as unvisited for backtracking
		path.remove(path.size() - 1);
		visited[row][col] = false;
	}

	public static void main(String[] args) {
		Solution solution = new Solution();
		int[][] grid = {
			{
				0, 0, 0
			},
			{
				0, 1, 0
			},
			{
				0, 0, 0
			}
		};
		List < List<int[] >> paths = solution.uniquePathsWithObstacles(grid);

		// Print all paths
		for (List < int[] > path: paths) {
			System.out.print("Path: ");

			for (int[] step: path) {
				System.out.print("[" + step[0] + "," + step[1] + "] ");
			}

			System.out.println();
		}
	}
}

Complexity

  • ⏰ Time complexity: O(4^(m*n))
  • 🧺 Space complexity: O(m*n)