The idea

Depth-First Search (DFS) is a graph traversal algorithm that explores as deeply as possible along each branch before backtracking to explore other options. This is similar to how we play a maze game.

DFS can be implemented iteratively using a stack data structure, similar to Breadth-First Search (BFS) which utilizes a queue. Alternatively, a recursive approach is very natural for DFS due to its depth-oriented exploration. We will explore both implementations in detail later.

Algorithm

A standard DFS implementation puts each vertex of the graph into one of two categories:

  1. Visited
  2. Not Visited

The purpose of the algorithm is to mark each vertex as visited while avoiding cycles.

Pseudocode

1
2
3
4
5

 DFS(graph G, vertex s)
     mark s as explored
     for every edge (s, v):
          if v unexplored
               DFS(G, v)

Iterative approach using Stack

Algorithm

The DFS algorithm works as follows:

  1. Start by putting any one of the graph’s vertices on top of a stack.
  2. Take the top item of the stack and add it to the visited list.
  3. Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the top of the stack.
  4. Keep repeating steps 2 and 3 until the stack is empty.

Pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

DFS-iterative (G, s): //Where G is graph and s is source vertex
 let S be stack
 S.push( s )//Inserting s in stack
 mark s as visited.
 while ( S is not empty):
    // Pop a vertex from stack to visit next
    v  =  S.top( )
   S.pop( )
   // Push all the neighbours of v in stack
   // that are not visited  
   for all neighbours w of v in Graph G:
       if w is not visited :
               S.push( w )        
               mark w as visited

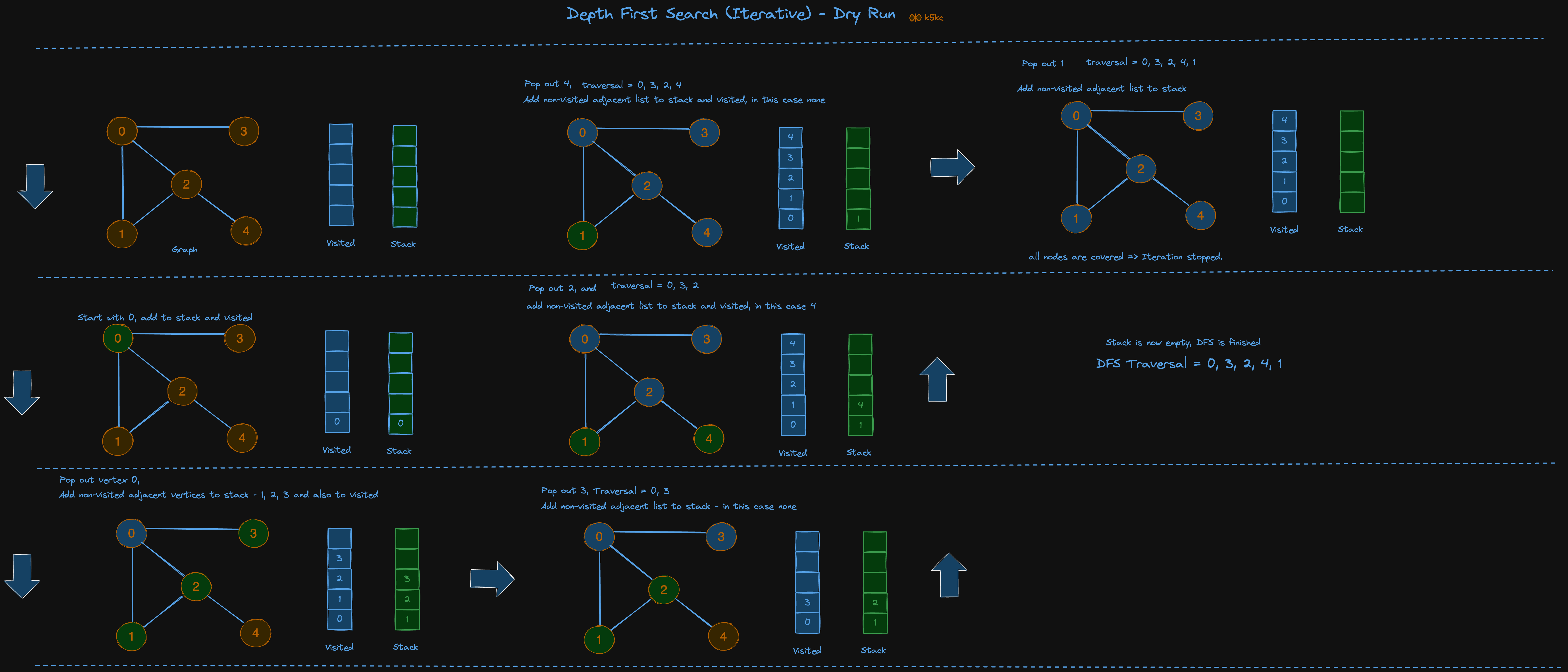
Dry-running Iterative DFS

Let’s see how the Depth First Search algorithm works with an example. We use an undirected graph with 5 vertices.

Code

Java

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

public List<Integer> DFS(ArrayList<ArrayList<Integer>> graph, int vertices) {
	boolean[] visited = new boolean[vertices+1];
	// Stack keeps track of which nodes we are visiting next
	Stack<Integer> stack = new Stack<Integer>();
	stack.push(1);
	visited[1] = true;
	List<Integer> dfsTraversal = new LinkedList<>();
	while (!stack.isEmpty()) {
		int current = stack.pop();
		dfsTraversal.add(current);
		List<Integer> neighbors = graph.get(current);
		for (int i = 0; i < neighbors.size(); i++) {
			int neighbor = neighbors.get(i);
			if (!visited[neighbor]) {
				visited[neighbor] = true;
				stack.push(neighbor);
			}
		}
	}
	return dfsTraversal;
}

Recursive approach

Algorithm

  • Maintain a visited[] to keep track of already visited vertices to avoid loops.
  • Start from the source vertex and make a recursive call to all the vertices which can be visited from the source and in recursive call, all these vertices will act a source.
  • See the code for more understanding.

Dry-running recursive DFS

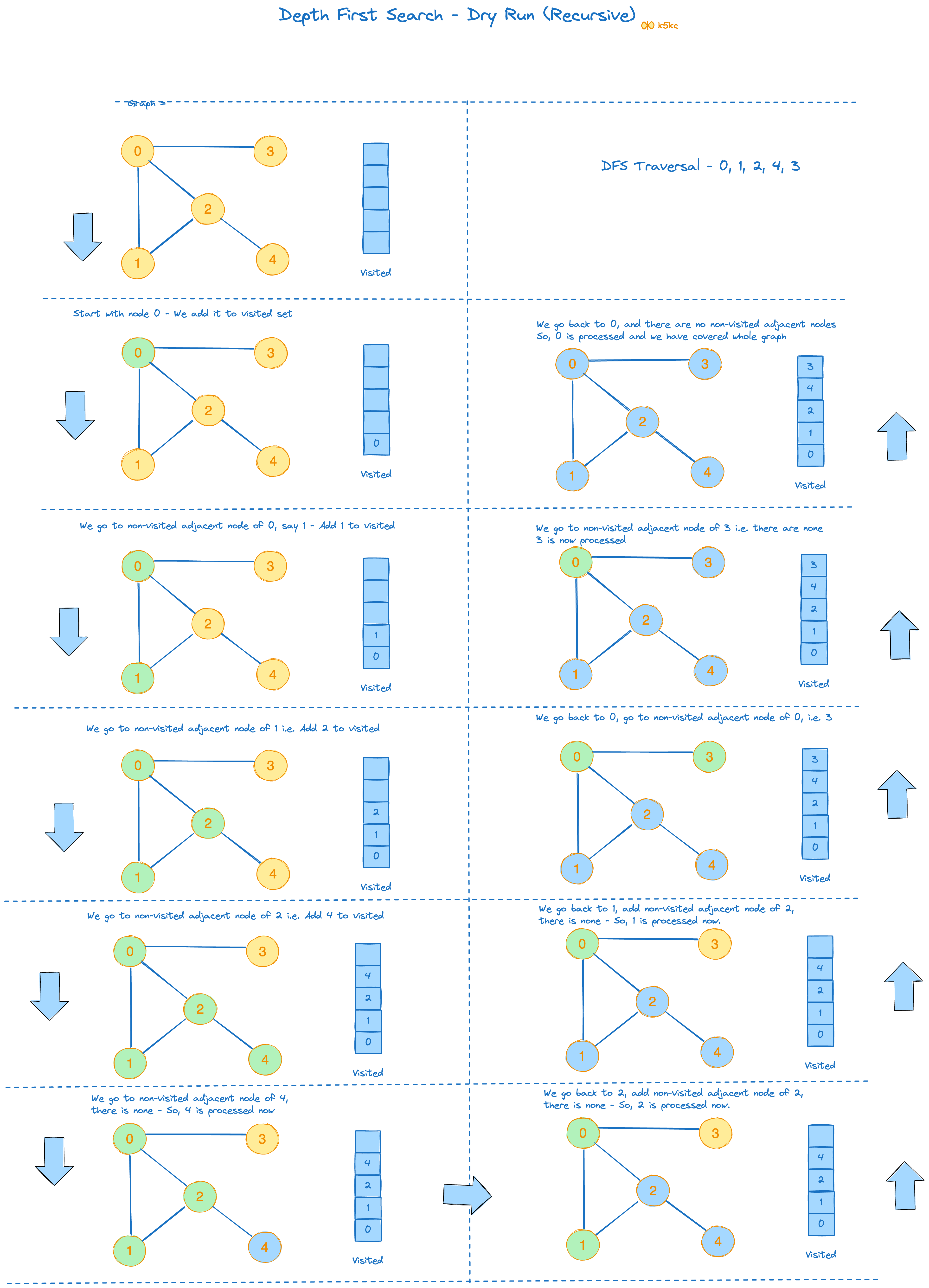
Think in terms of colouring

Initial graph node is yellow, then we add it to visited set and change color to green, and in end when we process it we make it blue.

Some, people also keep the node white initially, when it is visited, it is marked as grey, and finally when it is processed, it is black.

Code

Java

Simple Graph
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

public void DFSRecursion(int startVertex){
    boolean [] visited = new boolean[vertices];
    dfs(startVertex, visited);
}

public void dfs(int start, boolean [] visited){
    visited[start] = true;
    System.out.print(start + " ");
    for (int i = 0; i <adjList[start].size() ; i++) {
        int destination = adjList[start].get(i);
        if(!visited[destination])
            dfs(destination,visited);
    }
}
OOPs based graph

Here is the dfs recursion for oops based graph:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

public Set<Vertex> dfsRecursion(String startVertex){
    Set<Vertex> visited = new LinkedHashSet<>();
    dfs(Vertex.from(startVertex), visited);
    return visited;
}

private void dfs(Vertex start, Set<Vertex> visited){
    visited.add(start);

    System.out.print(start + " ");
    for (Edge e : start.getEdges()){
        Vertex destination = e.getTo();
        if (!visited.contains(destination)){
            dfs(destination, visited);
        }
    }
}

Video Explanation

Time Complexity

Running time for adjacency list- O(|V|+|E|) OR O(n+m) where |V| and |E| is number of vertices and edges for adjacency list representation of graph. Running time for adjacency matrix - O(|V|^2) OR O(n^2) as we have to traverse through the whole row until we find an edDepth First Searchsion]]

Applications of Depth First Traversal

  • Finding all the paths from root to leaf in a n-ary tree.
  • Finding all the connected components of the graph.
  • Solving Path finding in Mazes.
  • Topological Sorting.
  • Testing if graph is bi-partite
  • Check if path exists between 2 nodes in Graph