Problem

Design a data structure to store the strings’ count with the ability to return the strings with minimum and maximum counts.

Implement the AllOne class:

  • AllOne() Initializes the object of the data structure.
  • inc(String key) Increments the count of the string key by 1. If key does not exist in the data structure, insert it with count 1.
  • dec(String key) Decrements the count of the string key by 1. If the count of key is 0 after the decrement, remove it from the data structure. It is guaranteed that key exists in the data structure before the decrement.
  • getMaxKey() Returns one of the keys with the maximal count. If no element exists, return an empty string "".
  • getMinKey() Returns one of the keys with the minimum count. If no element exists, return an empty string "".

Note that each function must run in O(1) average time complexity.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

Input
["AllOne", "inc", "inc", "getMaxKey", "getMinKey", "inc", "getMaxKey", "getMinKey"]
[[], ["hello"], ["hello"], [], [], ["leet"], [], []]
Output
[null, null, null, "hello", "hello", null, "hello", "leet"]

Explanation
AllOne allOne = new AllOne();
allOne.inc("hello");
allOne.inc("hello");
allOne.getMaxKey(); // return "hello"
allOne.getMinKey(); // return "hello"
allOne.inc("leet");
allOne.getMaxKey(); // return "hello"
allOne.getMinKey(); // return "leet"

Solution

Method 1 - Using Map and DLL

Here is the summary of the approach:

  1. Data Structure Choice:

    • We use a doubly linked list (DLL) to maintain the counts of keys in an ordered manner. Each node in this list represents a unique count and holds a set of keys with that count.
    • A hashmap (dictionary in Python) maps each key to its corresponding node in the DLL, allowing O(1) access to the nodes.

  2. Doubly Linked List (DLL):

    • Each node in the DLL contains:
      • freq: The count value.
      • keys: A set of keys that have this count.
      • Pointers to the prev and next nodes.
    • We use sentinel nodes for the head (root.next) and tail (root.prev) to simplify boundary conditions.

  3. Increment (inc):

    • If the key does not exist, insert it with a count of 1 at the front i.e. using head pointer:
      • Find or create a node with count 1 at the front of the list.
    • If the key exists, increment its count:
      • Move the key to the next node with the incremented count.
      • If this next node does not exist, create it.
      • Remove the key from its current node and delete the node if it becomes empty.

  4. Decrement (dec):

    • The key is guaranteed to exist.
    • If the key’s count is 1, remove it from the structure.
    • Otherwise, decrement the count:
      • Move the key to the previous node with the decremented count.
      • If this previous node does not exist, create it.
      • Remove the key from its current node and delete the node if it becomes empty.

  5. Get Max Key (getMaxKey) and Get Min Key (getMinKey):

    • Directly access the keys in the tail node (root.prev) for the maximum count.
    • Access keys in the head node (root.next) for the minimum count.

Video explanation

Here is the video explaining this method in detail. Please check it out:

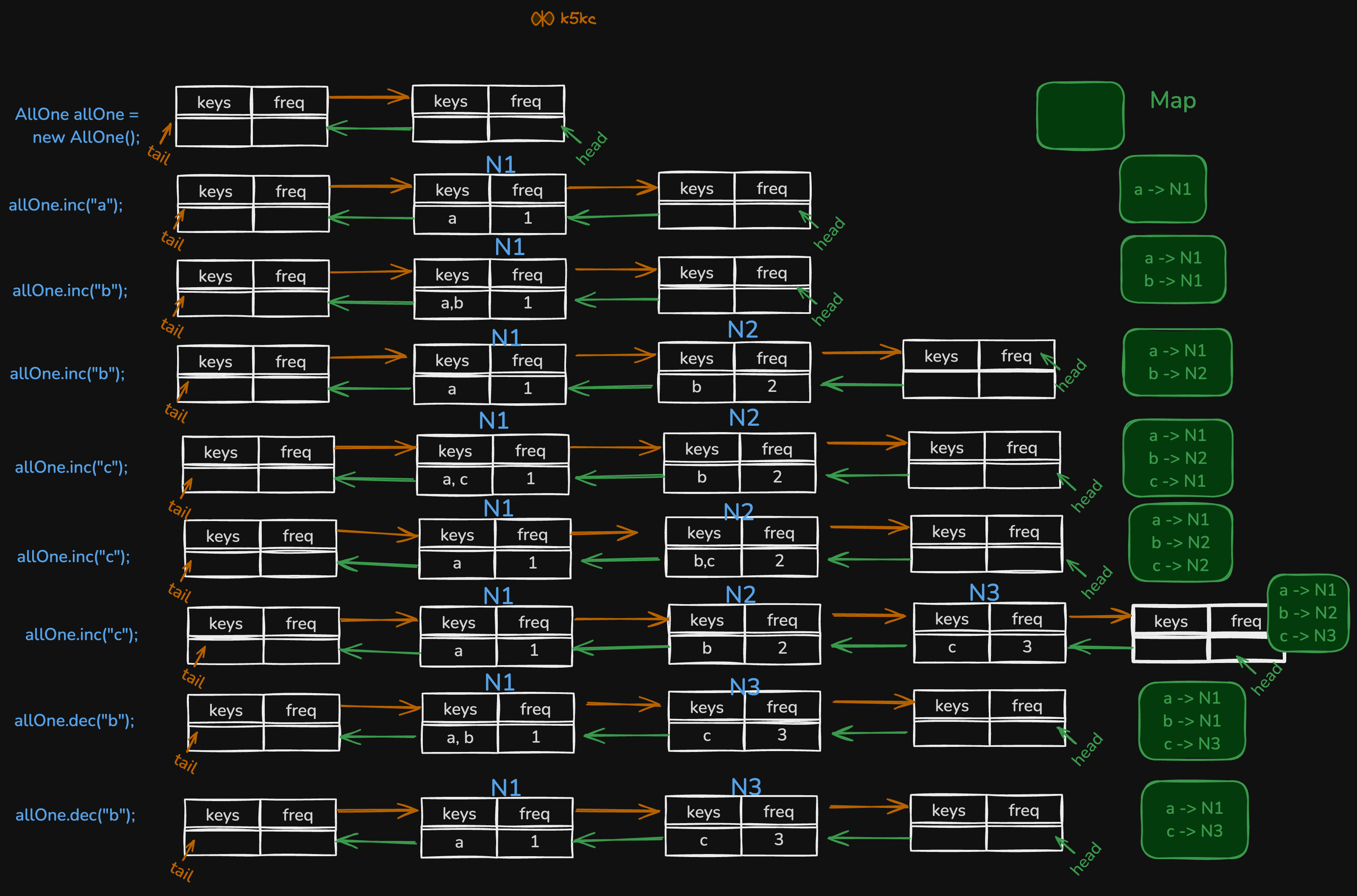
Dry Run

Here is an example dry run:

Code

1
2


##### Java
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105

class Node {
    Node prev;
    Node next;
    int freq;
    Set<String> keys = new HashSet<>();

    public Node() {
        this("", 0);
    }

    public Node(String key, int freq) {
        this.freq = freq;
        keys.add(key);
    }

    public void insert(Node node) {
        node.prev = this;
        node.next = this.next;
        node.prev.next = node;
        node.next.prev = node;
    }

    public void remove() {
        this.prev.next = this.next;
        this.next.prev = this.prev;
    }
}

class AllOne {
    private Node head = new Node(); // head sentinel
    private Node tail = new Node(); // tail sentinel
    private Map<String, Node> map = new HashMap<>();

    public AllOne() {
        tail.next = head;
        head.prev = tail;
    }

    public void inc(String key) {
        if (!map.containsKey(key)) {
            if (tail.next == head || tail.next.freq > 1) {
                Node newNode = new Node(key, 1);
                tail.insert(newNode);
                map.put(key, newNode);
            } else {
                tail.next.keys.add(key);
                map.put(key, tail.next);
            }
        } else {
            Node curr = map.get(key);
            Node next = curr.next;
            if (next == head || next.freq > curr.freq + 1) {
                Node newNode = new Node(key, curr.freq + 1);
                curr.insert(newNode);
                map.put(key, newNode);
            } else {
                next.keys.add(key);
                map.put(key, next);
            }
            curr.keys.remove(key);
            if (curr.keys.isEmpty()) {
                curr.remove();
            }
        }
    }

    public void dec(String key) {
        Node curr = map.get(key);
        if (curr.freq == 1) {
            map.remove(key);
        } else {
            Node prev = curr.prev;
            if (prev == tail || prev.freq < curr.freq - 1) {
                Node newNode = new Node(key, curr.freq - 1);
                prev.insert(newNode);
                map.put(key, newNode);
            } else {
                prev.keys.add(key);
                map.put(key, prev);
            }
        }
        curr.keys.remove(key);
        if (curr.keys.isEmpty()) {
            curr.remove();
        }
    }

    public String getMaxKey() {
        return tail.next != head ? head.prev.keys.iterator().next() : "";
    }

    public String getMinKey() {
        return tail.next != head ? tail.next.keys.iterator().next() : "";
    }

}

/**
 * Your AllOne object will be instantiated and called as such:
 * AllOne obj = new AllOne();
 * obj.inc(key);
 * obj.dec(key);
 * String param_3 = obj.getMaxKey();
 * String param_4 = obj.getMinKey();
 */
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

class Node:
    def __init__(self, key="", freq=0):
        self.prev = None
        self.next = None
        self.freq = freq
        self.keys = {key}

    def insert(self, node):
        node.prev = self
        node.next = self.next
        node.prev.next = node
        node.next.prev = node

    def remove(self):
        self.prev.next = self.next
        self.next.prev = self.prev


class AllOne:
    def __init__(self):
        self.head = Node()  # head sentinel
        self.tail = Node()  # tail sentinel
        self.tail.next = self.head
        self.head.prev = self.tail
        self.map = {}

    def _insert_node_after(self, new_node, prev_node):
        new_node.prev = prev_node
        new_node.next = prev_node.next
        prev_node.next.prev = new_node
        prev_node.next = new_node

    def inc(self, key: str) -> None:
        if key not in self.map:
            # Create and insert a new node with freq=1
            if self.tail.next == self.head or self.tail.next.freq > 1:
                new_node = Node(key, 1)
                self.tail.insert(new_node)
                self.map[key] = new_node
            else:
                self.tail.next.keys.add(key)
                self.map[key] = self.tail.next
        else:
            curr = self.map[key]
            next_node = curr.next
            # If the next node's freq is not curr.freq + 1, we need to insert a new node
            if next_node == self.head or next_node.freq > curr.freq + 1:
                new_node = Node(key, curr.freq + 1)
                curr.insert(new_node)
                self.map[key] = new_node
            else:
                next_node.keys.add(key)
                self.map[key] = next_node
            curr.keys.remove(key)
            if not curr.keys:
                curr.remove()

    def dec(self, key: str) -> None:
        curr = self.map[key]
        if curr.freq == 1:
            del self.map[key]
        else:
            prev_node = curr.prev
            if prev_node == self.tail or prev_node.freq < curr.freq - 1:
                new_node = Node(key, curr.freq - 1)
                prev_node.insert(new_node)
                self.map[key] = new_node
            else:
                prev_node.keys.add(key)
                self.map[key] = prev_node
        curr.keys.remove(key)
        if not curr.keys:
            curr.remove()

    def getMaxKey(self) -> str:
        return (
            next(iter(self.head.prev.keys), "")
            if self.tail.next != self.head
            else ""
        )

    def getMinKey(self) -> str:
        return (
            next(iter(self.tail.next.keys), "")
            if self.tail.next != self.head
            else ""
        )


# Your AllOne object will be instantiated and called as such:
# obj = AllOne()
# obj.inc(key)
# obj.dec(key)
# param_3 = obj.getMaxKey()
# param_4 = obj.getMinKey()

…

Complexity

  • Time: O(1)
  • Space: O(n), where n is number of keys in the data structure.