All Paths from Source to Target

Problem

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Examples

Example 1:

graph LR
   0 --> 1 & 2--> 3

Input:
graph = [[1,2],[3],[3],[]]
Output:
 [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

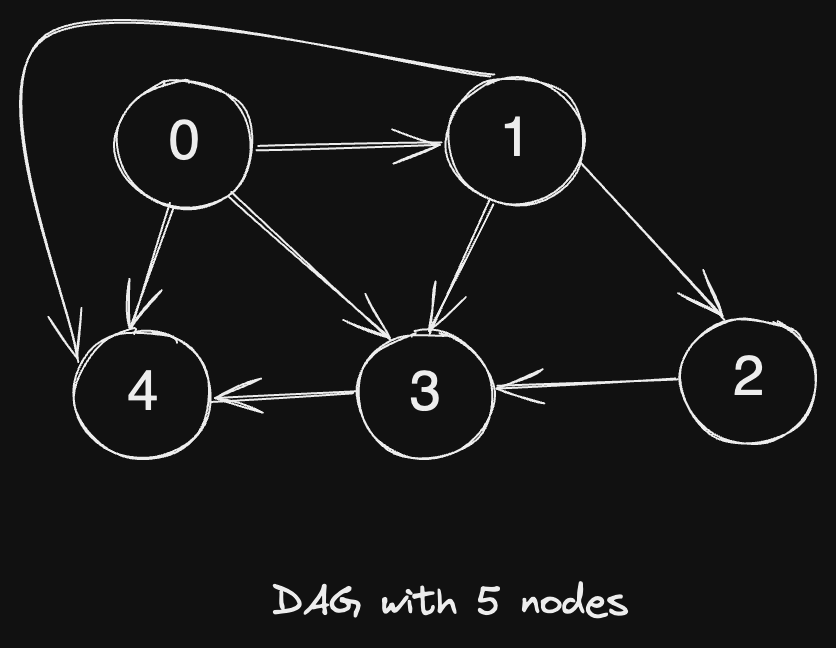
Input:
graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output:
 [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Solution

Method 1 – Backtracking (DFS)

Intuition

The key idea is to use depth-first search (DFS) to explore all possible paths from the source (node 0) to the target (node n-1). At each node, recursively visit all its neighbors, building up the current path. When the target is reached, add the path to the answer.

Approach

1. Start DFS from node 0 with an empty path.
2. At each node, add it to the current path.
3. If the node is the target (n-1), add a copy of the path to the answer.
4. Otherwise, recursively visit all neighbors.
5. Backtrack by removing the node from the path after visiting neighbors.

Code

C++

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> ans;
        vector<int> path;
        function<void(int)> dfs = [&](int u) {
            path.push_back(u);
            if (u == graph.size() - 1) ans.push_back(path);
            else for (int v : graph[u]) dfs(v);
            path.pop_back();
        };
        dfs(0);
        return ans;
    }
};

Go

func allPathsSourceTarget(graph [][]int) [][]int {
    var ans [][]int
    var path []int
    var dfs func(int)
    dfs = func(u int) {
        path = append(path, u)
        if u == len(graph)-1 {
            tmp := make([]int, len(path))
            copy(tmp, path)
            ans = append(ans, tmp)
        } else {
            for _, v := range graph[u] {
                dfs(v)
            }
        }
        path = path[:len(path)-1]
    }
    dfs(0)
    return ans
}

Java

class Solution {
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        dfs(0, graph, path, ans);
        return ans;
    }
    private void dfs(int u, int[][] graph, List<Integer> path, List<List<Integer>> ans) {
        path.add(u);
        if (u == graph.length - 1) ans.add(new ArrayList<>(path));
        else for (int v : graph[u]) dfs(v, graph, path, ans);
        path.remove(path.size() - 1);
    }
}

Kotlin

class Solution {
    fun allPathsSourceTarget(graph: Array<IntArray>): List<List<Int>> {
        val ans = mutableListOf<List<Int>>()
        val path = mutableListOf<Int>()
        fun dfs(u: Int) {
            path.add(u)
            if (u == graph.size - 1) ans.add(path.toList())
            else for (v in graph[u]) dfs(v)
            path.removeAt(path.size - 1)
        }
        dfs(0)
        return ans
    }
}

Python

class Solution:
    def allPathsSourceTarget(self, graph: list[list[int]]) -> list[list[int]]:
        ans = []
        path = []
        def dfs(u: int):
            path.append(u)
            if u == len(graph) - 1:
                ans.append(path[:])
            else:
                for v in graph[u]:
                    dfs(v)
            path.pop()
        dfs(0)
        return ans

Rust

impl Solution {
    pub fn all_paths_source_target(graph: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        fn dfs(u: usize, graph: &Vec<Vec<i32>>, path: &mut Vec<i32>, ans: &mut Vec<Vec<i32>>) {
            path.push(u as i32);
            if u == graph.len() - 1 {
                ans.push(path.clone());
            } else {
                for &v in &graph[u] {
                    dfs(v as usize, graph, path, ans);
                }
            }
            path.pop();
        }
        let mut ans = vec![];
        let mut path = vec![];
        dfs(0, &graph, &mut path, &mut ans);
        ans
    }
}

TypeScript

class Solution {
    allPathsSourceTarget(graph: number[][]): number[][] {
        const ans: number[][] = [];
        const path: number[] = [];
        const dfs = (u: number) => {
            path.push(u);
            if (u === graph.length - 1) ans.push([...path]);
            else for (const v of graph[u]) dfs(v);
            path.pop();
        };
        dfs(0);
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(2^n * n), since in the worst case (complete DAG), there are up to 2^(n-1) paths, each of length up to n.
• 🧺 Space complexity: O(2^n * n), for storing all paths and recursion stack.