problemhardalgorithmsleetcode-1478leetcode 1478leetcode1478

Allocate Mailboxes

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given the array houses where houses[i] is the location of the ith house along a street and an integer k, allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The test cases are generated so that the answer fits in a 32-bit integer.

Examples

Example 1

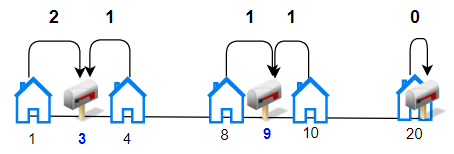
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5

Example 2

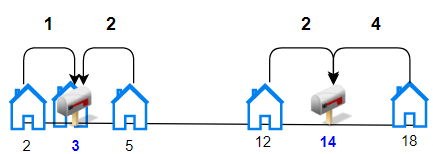
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

Solution

Method 1 – Dynamic Programming with Median Preprocessing

Intuition

The key idea is that for any group of houses, placing a mailbox at the median minimizes the sum of distances. We use dynamic programming to partition the houses into k groups, each covered by a mailbox, and minimize the total distance.

Approach

  1. Sort the Houses: Sorting ensures we can efficiently compute medians and groupings.
  2. Precompute Costs: For every subarray [i, j], compute the minimum distance to cover houses i to j with one mailbox (at the median).
  3. DP Definition: Let dp[i][k] be the minimum total distance to allocate k mailboxes among the first i houses.
  4. DP Transition: For each i and k, try placing the last mailbox covering houses j to i-1 and combine with the best solution for k-1 mailboxes among the first j houses.
  5. Initialization: dp[0][0] = 0 (zero houses, zero mailboxes).
  6. Result: The answer is dp[n][k], where n is the number of houses.

Code

C++
class Solution {
public:
  int minDistance(vector<int>& h, int k) {
    int n = h.size();
    sort(h.begin(), h.end());
    vector<vector<int>> cost(n, vector<int>(n));
    for (int i = 0; i < n; ++i)
      for (int j = i; j < n; ++j) {
        int m = (i + j) / 2, c = 0;
        for (int x = i; x <= j; ++x)
          c += abs(h[x] - h[m]);
        cost[i][j] = c;
      }
    vector<vector<int>> dp(n + 1, vector<int>(k + 1, 1e9));
    dp[0][0] = 0;
    for (int i = 1; i <= n; ++i)
      for (int m = 1; m <= k; ++m)
        for (int j = 0; j < i; ++j)
          dp[i][m] = min(dp[i][m], dp[j][m - 1] + cost[j][i - 1]);
    return dp[n][k];
  }
};
Go
func minDistance(h []int, k int) int {
  n := len(h)
  sort.Ints(h)
  cost := make([][]int, n)
  for i := range cost {
    cost[i] = make([]int, n)
    for j := i; j < n; j++ {
      m := (i + j) / 2
      c := 0
      for x := i; x <= j; x++ {
        c += abs(h[x] - h[m])
      }
      cost[i][j] = c
    }
  }
  dp := make([][]int, n+1)
  for i := range dp {
    dp[i] = make([]int, k+1)
    for j := range dp[i] {
      dp[i][j] = 1e9
    }
  }
  dp[0][0] = 0
  for i := 1; i <= n; i++ {
    for m := 1; m <= k; m++ {
      for j := 0; j < i; j++ {
        if dp[j][m-1]+cost[j][i-1] < dp[i][m] {
          dp[i][m] = dp[j][m-1] + cost[j][i-1]
        }
      }
    }
  }
  return dp[n][k]
}

func abs(a int) int {
  if a < 0 {
    return -a
  }
  return a
}
Java
class Solution {
  public int minDistance(int[] h, int k) {
    int n = h.length;
    Arrays.sort(h);
    int[][] cost = new int[n][n];
    for (int i = 0; i < n; ++i)
      for (int j = i; j < n; ++j) {
        int m = (i + j) / 2, c = 0;
        for (int x = i; x <= j; ++x)
          c += Math.abs(h[x] - h[m]);
        cost[i][j] = c;
      }
    int[][] dp = new int[n + 1][k + 1];
    for (int[] row : dp)
      Arrays.fill(row, 1000000000);
    dp[0][0] = 0;
    for (int i = 1; i <= n; ++i)
      for (int m = 1; m <= k; ++m)
        for (int j = 0; j < i; ++j)
          dp[i][m] = Math.min(dp[i][m], dp[j][m - 1] + cost[j][i - 1]);
    return dp[n][k];
  }
}
Kotlin
class Solution {
  fun minDistance(h: IntArray, k: Int): Int {
    val n = h.size
    h.sort()
    val cost = Array(n) { IntArray(n) }
    for (i in 0 until n)
      for (j in i until n) {
        val m = (i + j) / 2
        var c = 0
        for (x in i..j)
          c += kotlin.math.abs(h[x] - h[m])
        cost[i][j] = c
      }
    val dp = Array(n + 1) { IntArray(k + 1) { 1_000_000_000 } }
    dp[0][0] = 0
    for (i in 1..n)
      for (m in 1..k)
        for (j in 0 until i)
          dp[i][m] = minOf(dp[i][m], dp[j][m - 1] + cost[j][i - 1])
    return dp[n][k]
  }
}
Python
class Solution:
  def minDistance(self, h: list[int], k: int) -> int:
    n = len(h)
    h.sort()
    cost = [[0] * n for _ in range(n)]
    for i in range(n):
      for j in range(i, n):
        m = (i + j) // 2
        cost[i][j] = sum(abs(h[x] - h[m]) for x in range(i, j + 1))
    dp = [[float('inf')] * (k + 1) for _ in range(n + 1)]
    dp[0][0] = 0
    for i in range(1, n + 1):
      for m in range(1, k + 1):
        for j in range(i):
          dp[i][m] = min(dp[i][m], dp[j][m - 1] + cost[j][i - 1])
    return dp[n][k]
Rust
impl Solution {
  pub fn min_distance(mut h: Vec<i32>, k: i32) -> i32 {
    let n = h.len();
    h.sort();
    let mut cost = vec![vec![0; n]; n];
    for i in 0..n {
      for j in i..n {
        let m = (i + j) / 2;
        let mut c = 0;
        for x in i..=j {
          c += (h[x] - h[m]).abs();
        }
        cost[i][j] = c;
      }
    }
    let mut dp = vec![vec![1_000_000_000; (k + 1) as usize]; n + 1];
    dp[0][0] = 0;
    for i in 1..=n {
      for m in 1..=k as usize {
        for j in 0..i {
          dp[i][m] = dp[i][m].min(dp[j][m - 1] + cost[j][i - 1]);
        }
      }
    }
    dp[n][k as usize]
  }
}

Complexity

  • ⏰ Time complexity: O(n^3) (due to three nested loops for DP and cost preprocessing)
  • 🧺 Space complexity: O(n^2) (for cost and DP tables)

Comments