problemeasyalgorithmsleetcode-3206leetcode 3206leetcode3206alternating-groups-ialternating groups ialternatinggroupsi

Alternating Groups 1

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There is a circle of red and blue tiles. You are given an array of integers colors. The color of tile i is represented by colors[i]:

  • colors[i] == 0 means that tile i is red.
  • colors[i] == 1 means that tile i is blue.

Every 3 contiguous tiles in the circle with alternating colors (the middle tile has a different color from its left and right tiles) is called an alternating group.

Return the number of alternating groups.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

Examples

Example 1:

Input: colors = [1,1,1]
Output: 0
Explanation:

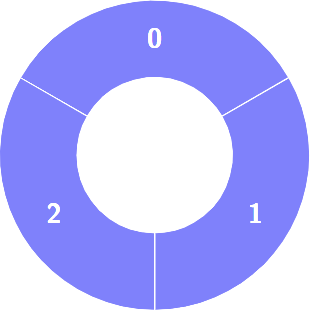
Example 2:

Input: colors = [0,1,0,0,1]
Output: 3
Explanation:

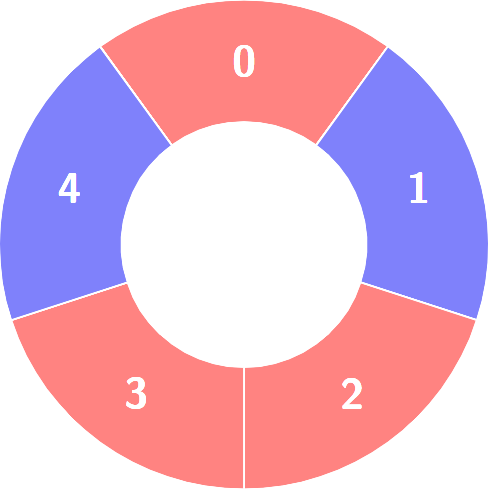Alternating groups:

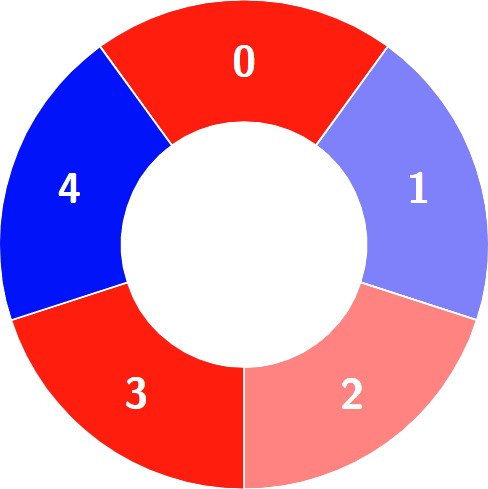
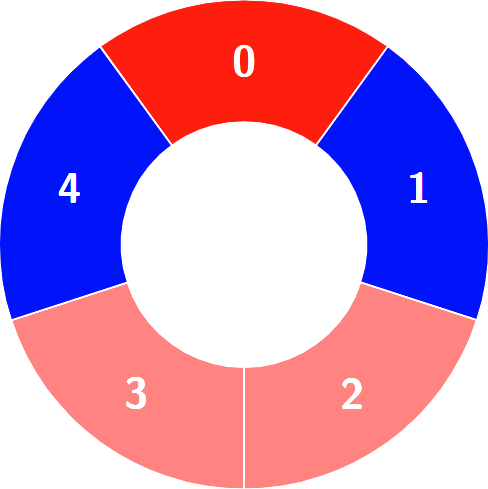
Constraints:

  • 3 <= colors.length <= 100
  • 0 <= colors[i] <= 1

Solution

Method 1 – Sliding Window with Modulo

Intuition

Since the tiles form a circle, we can use a sliding window of size 3 and wrap around using modulo. For each window, we check if the middle tile is different from both its neighbors. This way, we count all valid alternating groups efficiently.

Approach

  1. Let n be the length of colors.
  2. Initialize ans to 0.
  3. For each index i from 0 to n-1:
  • Let a = colors[i]
  • Let b = colors[(i+1)%n]
  • Let c = colors[(i+2)%n]
  • If b is different from both a and c, increment ans.
  1. Return ans.

Code

C++
class Solution {
public:
   int alternatingSubarrayGroups(vector<int>& colors) {
      int n = colors.size(), ans = 0;
      for (int i = 0; i < n; ++i) {
        int a = colors[i];
        int b = colors[(i+1)%n];
        int c = colors[(i+2)%n];
        if (b != a && b != c) ans++;
      }
      return ans;
   }
};
Java
class Solution {
   public int alternatingSubarrayGroups(int[] colors) {
      int n = colors.length, ans = 0;
      for (int i = 0; i < n; i++) {
        int a = colors[i];
        int b = colors[(i+1)%n];
        int c = colors[(i+2)%n];
        if (b != a && b != c) ans++;
      }
      return ans;
   }
}
Python
class Solution:
   def alternatingSubarrayGroups(self, colors: list[int]) -> int:
      n: int = len(colors)
      ans: int = 0
      for i in range(n):
        a: int = colors[i]
        b: int = colors[(i+1)%n]
        c: int = colors[(i+2)%n]
        if b != a and b != c:
           ans += 1
      return ans

Complexity

  • ⏰ Time complexity: O(N) — We check each possible group once.
  • 🧺 Space complexity: O(1) — Only a few variables are used.

Comments