problemmediumalgorithmsleetcode-3208leetcode 3208leetcode3208alternating-groups-iialternating groups iialternatinggroupsii

Alternating Groups 2

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented by colors[i]:

  • colors[i] == 0 means that tile i is red.
  • colors[i] == 1 means that tile i is blue.

An alternating group is every k contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).

Return the number of alternating groups.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

Examples

Example 1:

Input: colors = [0,1,0,1,0], k = 3
Output: 3
Explanation:

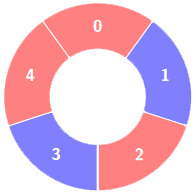
Alternating groups:

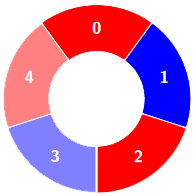
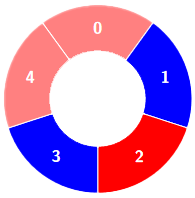
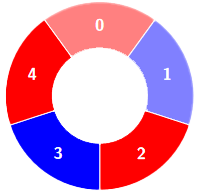
Example 2:


Input: colors = [0,1,0,0,1,0,1], k = 6

Output: 2

Explanation:

Alternating groups:

Example 3:


Input: colors = [1,1,0,1], k = 4

Output: 0

Explanation:

Constraints

  • 3 <= colors.length <= 105
  • 0 <= colors[i] <= 1
  • 3 <= k <= colors.length

Solution

First:

  • Colours are represented using integers: 0 for red, 1 for blue.
  • k is the size of the group to check.
  • The array colors represents a circular arrangement of tiles, meaning the last and first elements are adjacent in the circle.

Method 1 - Sliding Window

Here are group properties:

  • A group of size k is alternating if: - Each tile alternates in colour with its neighbours.
  • For a valid group:
    • If the first tile is 0 (red), the expected sequence alternates as 0, 1, 0, 1....
    • If the first tile is 1 (blue), the expected sequence alternates as 1, 0, 1, 0....

Because input is circular, extend the colours array by concatenating a copy of itself. This way, we can perform straightforward index-based checks across the potentially end-overlapping groups.

Algorithms

  • Extend the array by concatenating colors with itself.
  • Check all possible windows of size k in the extended array.
  • Compare each potential group with a valid alternating pattern.
  • Count the number of valid groups.

Code

Java
class Solution {
    public int countAlternatingGroups(int[] colors, int k) {
        int n = colors.length;
        int[] extColors = new int[2 * n];
        
        // Extend the array to handle circularity
        System.arraycopy(colors, 0, extColors, 0, n);
        System.arraycopy(colors, 0, extColors, n, n);

        int ans = 0;

        // Check all possible starting points in the original array
        for (int i = 0; i < n; i++) {
            if (isAlternating(extColors, i, k)) {
                ans++;
            }
        }

        return ans;
    }

    // Helper method to check if a group is alternating
    private boolean isAlternating(int[] extColors, int start, int k) {
        int expected = extColors[start];
        for (int i = 1; i < k; i++) {
            expected = 1 - expected; // Flip between 0 and 1
            if (extColors[start + i] != expected) {
                return false;
            }
        }
        return true;
    }
}
Python
class Solution:
    def countAlternatingGroups(self, colors: List[int], k: int) -> int:
        n: int = len(colors)
        ext_colors: List[int] = colors + colors  # Extend array to handle circularity
        ans: int = 0

        def is_alternating(start: int) -> bool:
            expected: int = ext_colors[start]
            for i in range(1, k):
                expected = 1 - expected  # Flip between 0 and 1
                if ext_colors[start + i] != expected:
                    return False
            return True

        # Check all possible starting points in the original array
        for i in range(n):  # Only 'n' checks are required due to circularity
            if is_alternating(i):
                ans += 1

        return ans

Complexity

  • ⏰ Time complexity: O(k * n), where k is sliding window size and n is size of the input array.
  • 🧺 Space complexity: O(n) as the extended array requires O(n) additional memory.

Comments