problemhardalgorithmsleetcode-3245leetcode 3245leetcode3245alternating-groups-iiialternating groups iiialternatinggroupsiii

Alternating Groups 3

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There are some red and blue tiles arranged circularly. You are given an array of integers colors and a 2D integers array queries.

The color of tile i is represented by colors[i]:

  • colors[i] == 0 means that tile i is red.
  • colors[i] == 1 means that tile i is blue.

An alternating group is a contiguous subset of tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its adjacent tiles in the group).

You have to process queries of two types:

  • queries[i] = [1, sizei], determine the count of alternating groups with size sizei.
  • queries[i] = [2, indexi, colori], change colors[indexi] to colori.

Return an array answer containing the results of the queries of the first type in order.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

Examples

Example 1:

Input: colors = [0,1,1,0,1], queries = [[2,1,0],[1,4]]
Output: [2]
Explanation:

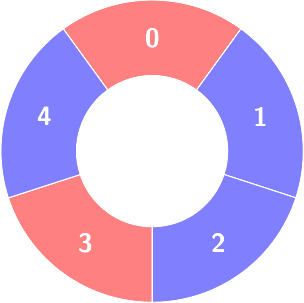** First query: Change colors[1] to 0.

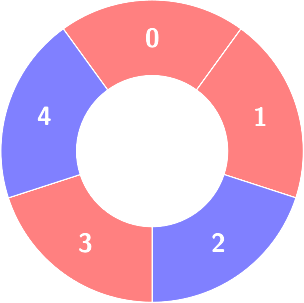
Second query: Count of the alternating groups with size 4:

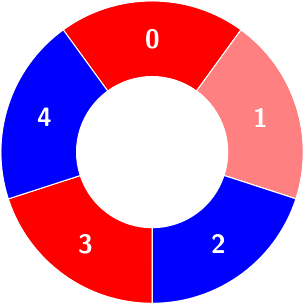
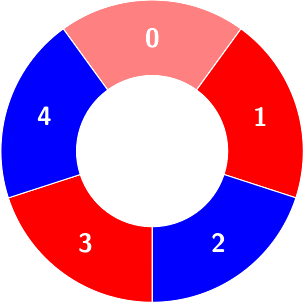
Example 2:

Input: colors = [0,0,1,0,1,1], queries = [[1,3],[2,3,0],[1,5]]
Output: [2,0]
Explanation:

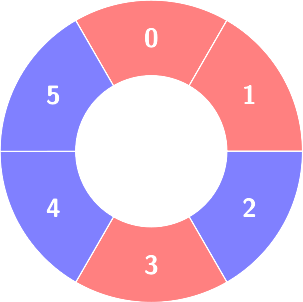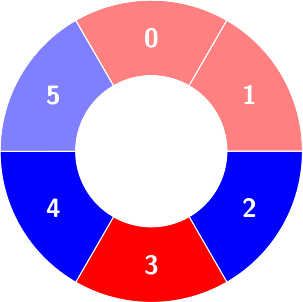
First query: Count of the alternating groups with size 3: Second query: colors will not change. Third query: There is no alternating group with size 5.

Constraints:

  • 4 <= colors.length <= 5 * 10^4
  • 0 <= colors[i] <= 1
  • 1 <= queries.length <= 5 * 104
  • queries[i][0] == 1 or queries[i][0] == 2
  • For all i that:
    • queries[i][0] == 1: queries[i].length == 2, 3 <= queries[i][1] <= colors.length - 1
    • queries[i][0] == 2: queries[i].length == 3, 0 <= queries[i][1] <= colors.length - 1, 0 <= queries[i][2] <= 1

Solution

Method 1 – Sliding Window with Circular Handling

Intuition

The key idea is to use a sliding window of the required size to check for alternating groups efficiently. Since the array is circular, we need to handle wrap-around cases. For updates, we simply change the color and process queries as needed.

Approach

  1. Sliding Window for Alternating Groups:
  • For a query [1, size], slide a window of length size over the array.
  • For each window, check if the colors alternate (i.e., adjacent tiles have different colors).
  • Since the array is circular, extend the array by concatenating the first size-1 elements to the end for wrap-around.
  • Count all valid windows.
  1. Processing Updates:
  • For a query [2, idx, color], update colors[idx] to color.
  1. Handling Queries:
  • Iterate through queries, process each according to its type, and collect answers for type 1 queries.
  1. Edge Cases:
  • Ensure window does not double-count groups due to circularity.
  • Only consider windows starting within the original array length.

Code

C++
class Solution {
public:
   vector<int> alternatingGroups(vector<int>& colors, vector<vector<int>>& queries) {
      int n = colors.size();
      vector<int> ans;
      for (auto& q : queries) {
        if (q[0] == 2) {
           colors[q[1]] = q[2];
        } else {
           int sz = q[1];
           int cnt = 0;
           // Create extended array for circular window
           vector<int> ext(colors.begin(), colors.end());
           ext.insert(ext.end(), colors.begin(), colors.begin() + sz - 1);
           for (int i = 0; i < n; ++i) {
              bool ok = true;
              for (int j = i + 1; j < i + sz; ++j) {
                if (ext[j] == ext[j - 1]) {
                   ok = false;
                   break;
                }
              }
              if (ok) cnt++;
           }
           ans.push_back(cnt);
        }
      }
      return ans;
   }
};
Java
class Solution {
   public List<Integer> alternatingGroups(int[] colors, int[][] queries) {
      int n = colors.length;
      List<Integer> ans = new ArrayList<>();
      for (int[] q : queries) {
        if (q[0] == 2) {
           colors[q[1]] = q[2];
        } else {
           int sz = q[1], cnt = 0;
           int[] ext = new int[n + sz - 1];
           System.arraycopy(colors, 0, ext, 0, n);
           System.arraycopy(colors, 0, ext, n, sz - 1);
           for (int i = 0; i < n; ++i) {
              boolean ok = true;
              for (int j = i + 1; j < i + sz; ++j) {
                if (ext[j] == ext[j - 1]) {
                   ok = false;
                   break;
                }
              }
              if (ok) cnt++;
           }
           ans.add(cnt);
        }
      }
      return ans;
   }
}
Python
class Solution:
   def alternatingGroups(self, colors: list[int], queries: list[list[int]]) -> list[int]:
      n = len(colors)
      ans: list[int] = []
      for q in queries:
        if q[0] == 2:
           colors[q[1]] = q[2]
        else:
           sz = q[1]
           cnt = 0
           ext = colors + colors[:sz-1]
           for i in range(n):
              ok = True
              for j in range(i+1, i+sz):
                if ext[j] == ext[j-1]:
                   ok = False
                   break
              if ok:
                cnt += 1
           ans.append(cnt)
      return ans

Complexity

  • ⏰ Time complexity: O(Q * N * S) where Q is the number of queries, N is the length of colors, and S is the group size (worst case up to N).
  • 🧺 Space complexity: O(N) for the extended array per query.

Comments