Problem

Given two numbers, hour and minutes, return the smaller angle (in degrees) formed between the hour and the minute hand.

Answers within 10^-5 of the actual value will be accepted as correct.

Examples

Example 1:

1
2

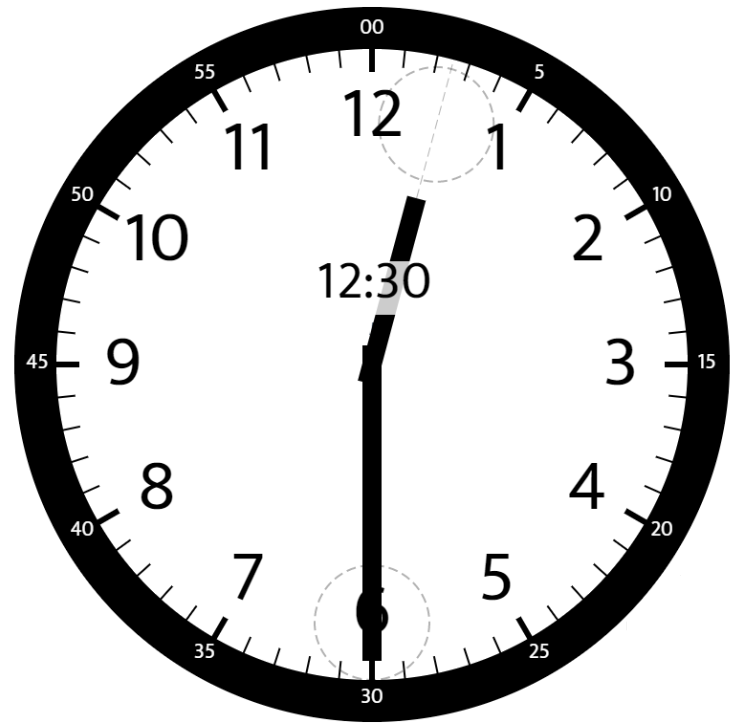
Input: hour = 12, minutes = 30
Output: 165

Example 2:

1
2

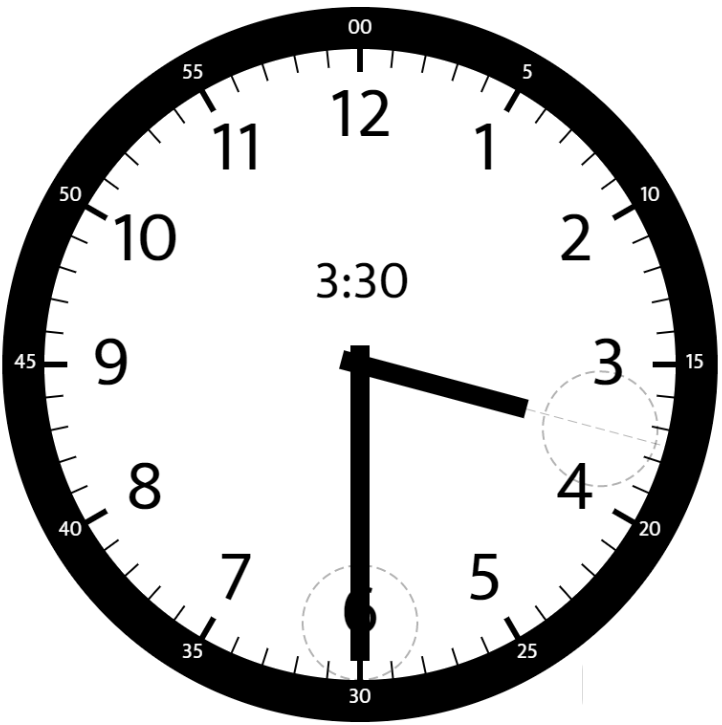
Input: hour = 3, minutes = 30
Output: 75

Example 3:

1
2

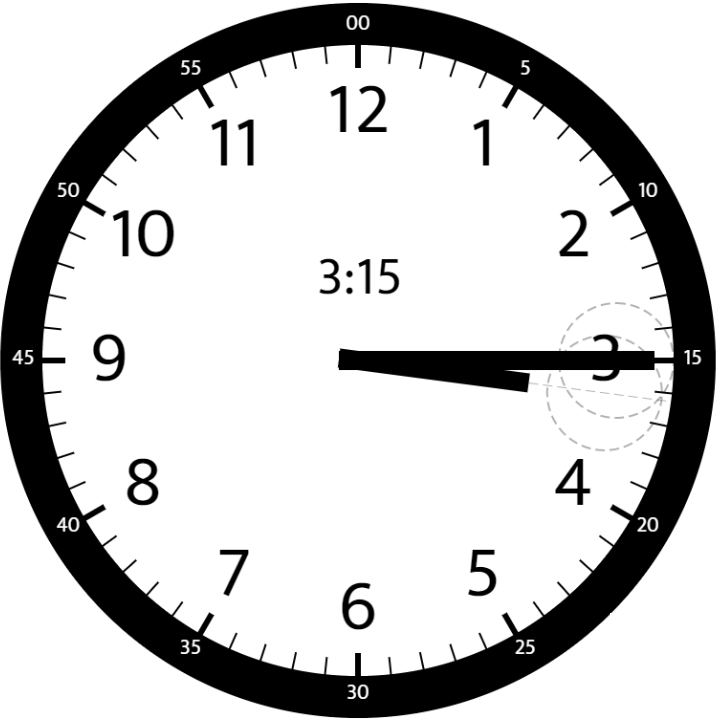
Input: hour = 3, minutes = 15
Output: 7.5

Constraints:

  • 1 <= hour <= 12
  • 0 <= minutes <= 59

Variant - Daily Coding Problem 303

Given a clock time in hh:mm format, determine, to the nearest degree, the angle between the hour and the minute hands.

Bonus: When, during the course of a day, will the angle be zero?

Example 1

1
2
3

Input: "12:30"
Output: 165
Explanation: Same as original example 1, but input is string format and output is rounded.

Example 2

1
2
3

Input: "03:15"
Output: 8
Explanation: Exact angle is 7.5°, rounded to nearest degree gives 8°.

Example 3

1
2
3

Input: "06:00"
Output: 180
Explanation: Hour hand at 180°, minute hand at 0°, difference is 180°.

Solution

Method 1 – Math Simulation

Intuition

The hour and minute hands move at different rates. By calculating their positions in degrees, we can find the absolute difference and ensure we return the smaller angle (≤180°). For example, at 3:15, the hour hand is at 97.5° and the minute hand at 90°, so the angle is 7.5°.

Approach

  1. Calculate the position of the hour hand:
  • Each hour is 30° (360°/12).
  • The hour hand also moves as minutes pass: each minute adds 0.5° (30°/60).
  • Formula: hour_angle = (hour % 12) * 30 + minutes * 0.5
  1. Calculate the position of the minute hand:
  • Each minute is 6° (360°/60).
  • Formula: minute_angle = minutes * 6
  1. Find the absolute difference between the two angles.
  2. Return the smaller angle (if >180°, subtract from 360°).

Code

1
2
3
4
5
6
7
8
9

class Solution {
public:
   double angleClock(int hour, int minutes) {
      double ha = (hour % 12) * 30 + minutes * 0.5;
      double ma = minutes * 6;
      double ans = abs(ha - ma);
      return ans > 180 ? 360 - ans : ans;
   }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

type Solution struct{}

func (Solution) AngleClock(hour int, minutes int) float64 {
   ha := float64(hour%12)*30 + float64(minutes)*0.5
   ma := float64(minutes) * 6
   ans := ha - ma
   if ans < 0 {
      ans = -ans
   }
   if ans > 180 {
      return 360 - ans
   }
   return ans
}
1
2
3
4
5
6
7
8

class Solution {
   public double angleClock(int hour, int minutes) {
      double ha = (hour % 12) * 30 + minutes * 0.5;
      double ma = minutes * 6;
      double ans = Math.abs(ha - ma);
      return ans > 180 ? 360 - ans : ans;
   }
}
1
2
3
4
5
6
7
8

class Solution {
   fun angleClock(hour: Int, minutes: Int): Double {
      val ha = (hour % 12) * 30 + minutes * 0.5
      val ma = minutes * 6.0
      val ans = kotlin.math.abs(ha - ma)
      return if (ans > 180) 360 - ans else ans
   }
}
1
2
3
4
5
6

class Solution:
   def angleClock(self, hour: int, minutes: int) -> float:
      ha: float = (hour % 12) * 30 + minutes * 0.5
      ma: float = minutes * 6
      ans: float = abs(ha - ma)
      return 360 - ans if ans > 180 else ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

impl Solution {
   pub fn angle_clock(hour: i32, minutes: i32) -> f64 {
      let ha = (hour % 12) as f64 * 30.0 + minutes as f64 * 0.5;
      let ma = minutes as f64 * 6.0;
      let mut ans = (ha - ma).abs();
      if ans > 180.0 {
        ans = 360.0 - ans;
      }
      ans
   }
}

Complexity

  • ⏰ Time complexity: O(1) (constant time arithmetic)
  • 🧺 Space complexity: O(1) (no extra space)

Variant Solution

Method 2 - String Input with Rounding

Intuition

This variant takes time as a string and rounds the result to the nearest degree. The core calculation remains the same, but we need to parse the input and round the output. For the bonus question, we need to find when both hands overlap.

Approach

  1. Parse the hh:mm string to extract hour and minutes
  2. Use the same angle calculation as Method 1
  3. Round the result to the nearest degree using standard rounding
  4. For bonus: hands overlap when their angles are equal, which happens 11 times in 12 hours

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
public:
    int angleClockFromString(string time) {
        int colon = time.find(':');
        int hour = stoi(time.substr(0, colon));
        int minutes = stoi(time.substr(colon + 1));
        
        double ha = (hour % 12) * 30 + minutes * 0.5;
        double ma = minutes * 6;
        double ans = abs(ha - ma);
        if (ans > 180) ans = 360 - ans;
        
        return round(ans);
    }
    
    vector<string> getZeroAngleTimes() {
        vector<string> times;
        // Hands overlap 11 times in 12 hours
        for (int i = 0; i < 11; i++) {
            double minutes = i * 720.0 / 11; // 720 minutes in 12 hours / 11 overlaps
            int h = (int)(minutes / 60) % 12;
            int m = (int)(minutes) % 60;
            int s = (int)((minutes - (int)minutes) * 60);
            
            char buffer[10];
            sprintf(buffer, "%02d:%02d:%02d", h == 0 ? 12 : h, m, s);
            times.push_back(string(buffer));
        }
        return times;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func angleClockFromString(time string) int {
    parts := strings.Split(time, ":")
    hour, _ := strconv.Atoi(parts[0])
    minutes, _ := strconv.Atoi(parts[1])
    
    ha := float64(hour%12)*30 + float64(minutes)*0.5
    ma := float64(minutes) * 6
    ans := math.Abs(ha - ma)
    if ans > 180 {
        ans = 360 - ans
    }
    
    return int(math.Round(ans))
}

func getZeroAngleTimes() []string {
    var times []string
    // Hands overlap 11 times in 12 hours
    for i := 0; i < 11; i++ {
        minutes := float64(i) * 720.0 / 11 // 720 minutes in 12 hours / 11 overlaps
        h := int(minutes/60) % 12
        m := int(minutes) % 60
        s := int((minutes - float64(int(minutes))) * 60)
        
        if h == 0 {
            h = 12
        }
        times = append(times, fmt.Sprintf("%02d:%02d:%02d", h, m, s))
    }
    return times
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    public int angleClockFromString(String time) {
        String[] parts = time.split(":");
        int hour = Integer.parseInt(parts[0]);
        int minutes = Integer.parseInt(parts[1]);
        
        double ha = (hour % 12) * 30 + minutes * 0.5;
        double ma = minutes * 6;
        double ans = Math.abs(ha - ma);
        if (ans > 180) ans = 360 - ans;
        
        return (int) Math.round(ans);
    }
    
    public List<String> getZeroAngleTimes() {
        List<String> times = new ArrayList<>();
        // Hands overlap 11 times in 12 hours
        for (int i = 0; i < 11; i++) {
            double minutes = i * 720.0 / 11; // 720 minutes in 12 hours / 11 overlaps
            int h = (int)(minutes / 60) % 12;
            int m = (int)(minutes) % 60;
            int s = (int)((minutes - (int)minutes) * 60);
            
            times.add(String.format("%02d:%02d:%02d", h == 0 ? 12 : h, m, s));
        }
        return times;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution:
    def angleClockFromString(self, time: str) -> int:
        hour, minutes = map(int, time.split(':'))
        
        ha: float = (hour % 12) * 30 + minutes * 0.5
        ma: float = minutes * 6
        ans: float = abs(ha - ma)
        if ans > 180:
            ans = 360 - ans
        
        return round(ans)
    
    def getZeroAngleTimes(self) -> List[str]:
        times = []
        # Hands overlap 11 times in 12 hours
        for i in range(11):
            minutes = i * 720 / 11  # 720 minutes in 12 hours / 11 overlaps
            h = int(minutes // 60) % 12
            m = int(minutes) % 60
            s = int((minutes - int(minutes)) * 60)
            
            times.append(f"{h if h != 0 else 12:02d}:{m:02d}:{s:02d}")
        return times

Complexity

  • ⏰ Time complexity: O(1) for angle calculation, O(1) for zero angle times (fixed 11 iterations)
  • 🧺 Space complexity: O(1) for angle calculation, O(1) for zero angle times (fixed size result)

Bonus Answer - Zero Angle Times

The clock hands overlap (angle = 0°) exactly 11 times during a 12-hour period:

  1. 12:00:00 (start)
  2. 01:05:27 (approximately)
  3. 02:10:55 (approximately)
  4. 03:16:22 (approximately)
  5. 04:21:49 (approximately)
  6. 05:27:16 (approximately)
  7. 06:32:44 (approximately)
  8. 07:38:11 (approximately)
  9. 08:43:38 (approximately)
  10. 09:49:05 (approximately)
  11. 10:54:33 (approximately)

Formula: The hands overlap every 720/11 ≈ 65.45 minutes, starting from 12:00.

Mathematical Explanation:

  • Hour hand moves at 0.5°/minute
  • Minute hand moves at 6°/minute
  • Relative speed = 6 - 0.5 = 5.5°/minute
  • Time for minute hand to “lap” hour hand = 360°/5.5° = 720/11 minutes ≈ 65.45 minutes