problemeasyalgorithmsleetcode-637leetcode 637leetcode637

Average of Levels in Binary Tree

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.

Examples

Example 1

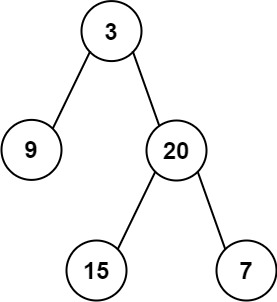
Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].

Example 2

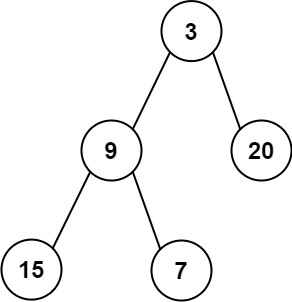
Input: root = [3,9,20,15,7]
Output: [3.00000,14.50000,11.00000]

Constraints

  • The number of nodes in the tree is in the range [1, 10^4].
  • -2^31 <= Node.val <= 2^31 - 1

Solution

Method 1 – Level Order Traversal (BFS)

Intuition

The key idea is to process the tree level by level using a queue (Breadth-First Search). For each level, sum the node values and divide by the number of nodes at that level to get the average.

Approach

  1. Initialize an empty list ans to store averages.
  2. Use a queue to perform BFS, starting with the root node.
  3. While the queue is not empty:
  • Record the number of nodes at the current level.
  • For each node at this level:
    • Pop it from the queue.
    • Add its value to a running sum.
    • Add its children to the queue if they exist.
  • Compute the average for this level and append to ans.
  1. Return ans.

Code

C++
class Solution {
public:
   vector<double> averageOfLevels(TreeNode* root) {
      vector<double> ans;
      queue<TreeNode*> q;
      q.push(root);
      while (!q.empty()) {
        int n = q.size();
        double sum = 0;
        for (int i = 0; i < n; ++i) {
           TreeNode* node = q.front(); q.pop();
           sum += node->val;
           if (node->left) q.push(node->left);
           if (node->right) q.push(node->right);
        }
        ans.push_back(sum / n);
      }
      return ans;
   }
};
Go
func averageOfLevels(root *TreeNode) []float64 {
   var ans []float64
   q := []*TreeNode{root}
   for len(q) > 0 {
      n := len(q)
      sum := 0
      for i := 0; i < n; i++ {
        node := q[0]
        q = q[1:]
        sum += node.Val
        if node.Left != nil {
           q = append(q, node.Left)
        }
        if node.Right != nil {
           q = append(q, node.Right)
        }
      }
      ans = append(ans, float64(sum)/float64(n))
   }
   return ans
}
Java
class Solution {
   public List<Double> averageOfLevels(TreeNode root) {
      List<Double> ans = new ArrayList<>();
      Queue<TreeNode> q = new LinkedList<>();
      q.offer(root);
      while (!q.isEmpty()) {
        int n = q.size();
        double sum = 0;
        for (int i = 0; i < n; i++) {
           TreeNode node = q.poll();
           sum += node.val;
           if (node.left != null) q.offer(node.left);
           if (node.right != null) q.offer(node.right);
        }
        ans.add(sum / n);
      }
      return ans;
   }
}
Kotlin
class Solution {
   fun averageOfLevels(root: TreeNode?): List<Double> {
      val ans = mutableListOf<Double>()
      val q = ArrayDeque<TreeNode>()
      if (root != null) q.add(root)
      while (q.isNotEmpty()) {
        val n = q.size
        var sum = 0.0
        repeat(n) {
           val node = q.removeFirst()
           sum += node.`val`
           node.left?.let { q.add(it) }
           node.right?.let { q.add(it) }
        }
        ans.add(sum / n)
      }
      return ans
   }
}
Python
class Solution:
   def averageOfLevels(self, root: Optional[TreeNode]) -> list[float]:
      ans: list[float] = []
      q: list[TreeNode] = [root]
      while q:
        n = len(q)
        s = 0
        for _ in range(n):
           node = q.pop(0)
           s += node.val
           if node.left:
              q.append(node.left)
           if node.right:
              q.append(node.right)
        ans.append(s / n)
      return ans
Rust
impl Solution {
   pub fn average_of_levels(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<f64> {
      let mut ans = vec![];
      let mut q = vec![];
      if let Some(node) = root {
        q.push(node);
      }
      while !q.is_empty() {
        let n = q.len();
        let mut sum = 0f64;
        let mut next = vec![];
        for node in q {
           let node = node.borrow();
           sum += node.val as f64;
           if let Some(ref l) = node.left {
              next.push(Rc::clone(l));
           }
           if let Some(ref r) = node.right {
              next.push(Rc::clone(r));
           }
        }
        ans.push(sum / n as f64);
        q = next;
      }
      ans
   }
}

Complexity

  • ⏰ Time complexity: O(N) where N is the number of nodes (each node is visited once).
  • 🧺 Space complexity: O(W) where W is the maximum width of the tree (max number of nodes at any level).

Comments