Binary Search Tree Iterator II

Problem

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.
boolean hasPrev() Returns true if there exists a number in the traversal to the left of the pointer, otherwise returns false.
int prev() Moves the pointer to the left, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() and prev() calls will always be valid. That is, there will be at least a next/previous number in the in-order traversal when next()/prev() is called.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


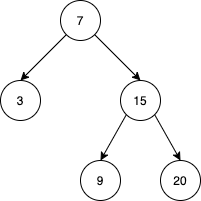
Input
["BSTIterator", "next", "next", "prev", "next", "hasNext", "next", "next", "next", "hasNext", "hasPrev", "prev", "prev"]
[[[7, 3, 15, null, null, 9, 20]], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null]]
Output
[null, 3, 7, 3, 7, true, 9, 15, 20, false, true, 15, 9]

Explanation
// The underlined element is where the pointer currently is.
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); // state is __ [3, 7, 9, 15, 20]
bSTIterator.next(); // state becomes [_3_ , 7, 9, 15, 20], return 3
bSTIterator.next(); // state becomes [3, _7_ , 9, 15, 20], return 7
bSTIterator.prev(); // state becomes [_3_ , 7, 9, 15, 20], return 3
bSTIterator.next(); // state becomes [3, _7_ , 9, 15, 20], return 7
bSTIterator.hasNext(); // return true
bSTIterator.next(); // state becomes [3, 7, _9_ , 15, 20], return 9
bSTIterator.next(); // state becomes [3, 7, 9, _15_ , 20], return 15
bSTIterator.next(); // state becomes [3, 7, 9, 15, _20_], return 20
bSTIterator.hasNext(); // return false
bSTIterator.hasPrev(); // return true
bSTIterator.prev(); // state becomes [3, 7, 9, _15_ , 20], return 15
bSTIterator.prev(); // state becomes [3, 7, _9_ , 15, 20], return 9

Constraints:

The number of nodes in the tree is in the range [1, 105].
0 <= Node.val <= 10^6
At most 105 calls will be made to hasNext, next, hasPrev, and prev.

Follow up: Could you solve the problem without precalculating the values of the tree?

Solution

Method 1 – Inorder Traversal with List Buffer

Intuition

We can store the inorder traversal of the BST in a list, then use a pointer to move back and forth for next() and prev(). This allows O(1) time for all operations after the initial traversal.

Approach

Do an inorder traversal of the BST and store the values in a list.
Use an index pointer to track the current position.
next() increments the pointer and returns the value.
prev() decrements the pointer and returns the value.
hasNext() and hasPrev() check pointer bounds.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class BSTIterator {
    vector<int> vals;
    int idx;
    void inorder(TreeNode* node) {
        if (!node) return;
        inorder(node->left);
        vals.push_back(node->val);
        inorder(node->right);
    }
public:
    BSTIterator(TreeNode* root) : idx(-1) {
        inorder(root);
    }
    bool hasNext() { return idx + 1 < (int)vals.size(); }
    int next() { return vals[++idx]; }
    bool hasPrev() { return idx > 0; }
    int prev() { return vals[--idx]; }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


type BSTIterator struct {
    vals []int
    idx  int
}

func inorder(node *TreeNode, vals *[]int) {
    if node == nil { return }
    inorder(node.Left, vals)
    *vals = append(*vals, node.Val)
    inorder(node.Right, vals)
}

func Constructor(root *TreeNode) BSTIterator {
    vals := []int{}
    inorder(root, &vals)
    return BSTIterator{vals, -1}
}

func (it *BSTIterator) HasNext() bool { return it.idx+1 < len(it.vals) }
func (it *BSTIterator) Next() int { it.idx++; return it.vals[it.idx] }
func (it *BSTIterator) HasPrev() bool { return it.idx > 0 }
func (it *BSTIterator) Prev() int { it.idx--; return it.vals[it.idx] }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class BSTIterator {
    List<Integer> vals = new ArrayList<>();
    int idx = -1;
    void inorder(TreeNode node) {
        if (node == null) return;
        inorder(node.left);
        vals.add(node.val);
        inorder(node.right);
    }
    public BSTIterator(TreeNode root) {
        inorder(root);
    }
    public boolean hasNext() { return idx + 1 < vals.size(); }
    public int next() { return vals.get(++idx); }
    public boolean hasPrev() { return idx > 0; }
    public int prev() { return vals.get(--idx); }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class BSTIterator(root: TreeNode?) {
    private val vals = mutableListOf<Int>()
    private var idx = -1
    init {
        fun inorder(node: TreeNode?) {
            if (node == null) return
            inorder(node.left)
            vals.add(node.`val`)
            inorder(node.right)
        }
        inorder(root)
    }
    fun hasNext() = idx + 1 < vals.size
    fun next() = vals[++idx]
    fun hasPrev() = idx > 0
    fun prev() = vals[--idx]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


from typing import Optional
class BSTIterator:
    def __init__(self, root: 'Optional[TreeNode]'):
        self.vals = []
        self._inorder(root)
        self.idx = -1
    def _inorder(self, node):
        if not node: return
        self._inorder(node.left)
        self.vals.append(node.val)
        self._inorder(node.right)
    def hasNext(self) -> bool:
        return self.idx + 1 < len(self.vals)
    def next(self) -> int:
        self.idx += 1
        return self.vals[self.idx]
    def hasPrev(self) -> bool:
        return self.idx > 0
    def prev(self) -> int:
        self.idx -= 1
        return self.vals[self.idx]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


struct BSTIterator {
    vals: Vec<i32>,
    idx: isize,
}
impl BSTIterator {
    fn new(root: Option<Rc<RefCell<TreeNode>>>) -> Self {
        fn inorder(node: Option<Rc<RefCell<TreeNode>>>, vals: &mut Vec<i32>) {
            if let Some(n) = node {
                inorder(n.borrow().left.clone(), vals);
                vals.push(n.borrow().val);
                inorder(n.borrow().right.clone(), vals);
            }
        }
        let mut vals = vec![];
        inorder(root, &mut vals);
        BSTIterator { vals, idx: -1 }
    }
    fn has_next(&self) -> bool { (self.idx + 1) < self.vals.len() as isize }
    fn next(&mut self) -> i32 { self.idx += 1; self.vals[self.idx as usize] }
    fn has_prev(&self) -> bool { self.idx > 0 }
    fn prev(&mut self) -> i32 { self.idx -= 1; self.vals[self.idx as usize] }
}

Complexity

⏰ Time complexity: O(n) for construction, O(1) per operation
🧺 Space complexity: O(n) for storing the inorder traversal

Problem#

Examples#

Solution#

Method 1 – Inorder Traversal with List Buffer#

Intuition#

Approach#

Code#

Complexity#