Problem

Two players play a turn based game on a binary tree. We are given the root of this binary tree, and the number of nodes n in the tree. n is odd, and each node has a distinct value from 1 to n.

Initially, the first player names a value x with 1 <= x <= n, and the second player names a value y with 1 <= y <= n and y != x. The first player colors the node with value x red, and the second player colors the node with value y blue.

Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an uncolored neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)

If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.

You are the second player. If it is possible to choose such a y to ensure you win the game, return true. If it is not possible, return false.

Examples

Example 1

1
2
3

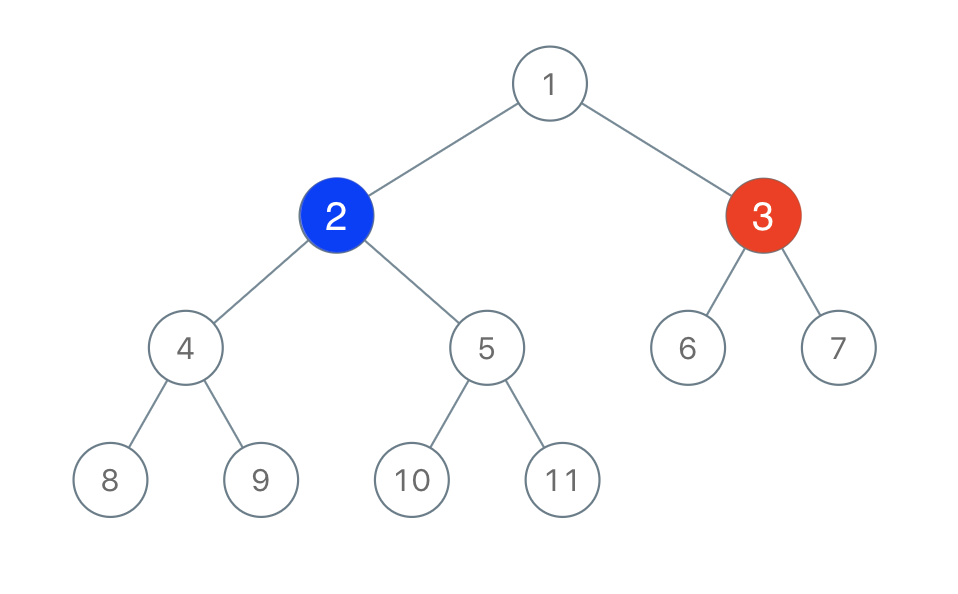
Input: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
Output: true
Explanation: The second player can choose the node with value 2.

Example 2

1
2

Input: root = [1,2,3], n = 3, x = 1
Output: false

Constraints

  • The number of nodes in the tree is n.
  • 1 <= x <= n <= 100
  • n is odd.
  • 1 <= Node.val <= n
  • All the values of the tree are unique.

Solution

Method 1 – Subtree Size Counting (DFS)

Intuition

The second player can win if they can control more than half of the nodes by picking a node in the left or right subtree of the node chosen by the first player, or the rest of the tree. We use DFS to count the size of the left and right subtrees of the node with value x.

Approach

  1. Traverse the tree to find the node with value x.
  2. Use DFS to count the size of the left and right subtrees of x.
  3. The rest of the nodes are n - (left + right + 1).
  4. The second player can win if any of these three regions has more than n/2 nodes.
  5. Return true if so, else false.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    int l = 0, r = 0;
    int dfs(TreeNode* node, int x) {
        if (!node) return 0;
        int left = dfs(node->left, x);
        int right = dfs(node->right, x);
        if (node->val == x) { l = left; r = right; }
        return left + right + 1;
    }
    bool btreeGameWinningMove(TreeNode* root, int n, int x) {
        dfs(root, x);
        int rest = n - (l + r + 1);
        return max({l, r, rest}) > n / 2;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func btreeGameWinningMove(root *TreeNode, n, x int) bool {
    var l, r int
    var dfs func(*TreeNode) int
    dfs = func(node *TreeNode) int {
        if node == nil { return 0 }
        left := dfs(node.Left)
        right := dfs(node.Right)
        if node.Val == x { l, r = left, right }
        return left + right + 1
    }
    dfs(root)
    rest := n - (l + r + 1)
    return max(l, max(r, rest)) > n/2
}
func max(a, b int) int { if a > b { return a }; return b }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    int l = 0, r = 0;
    public int dfs(TreeNode node, int x) {
        if (node == null) return 0;
        int left = dfs(node.left, x);
        int right = dfs(node.right, x);
        if (node.val == x) { l = left; r = right; }
        return left + right + 1;
    }
    public boolean btreeGameWinningMove(TreeNode root, int n, int x) {
        dfs(root, x);
        int rest = n - (l + r + 1);
        return Math.max(Math.max(l, r), rest) > n / 2;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    var l = 0
    var r = 0
    fun dfs(node: TreeNode?, x: Int): Int {
        if (node == null) return 0
        val left = dfs(node.left, x)
        val right = dfs(node.right, x)
        if (node.`val` == x) { l = left; r = right }
        return left + right + 1
    }
    fun btreeGameWinningMove(root: TreeNode?, n: Int, x: Int): Boolean {
        dfs(root, x)
        val rest = n - (l + r + 1)
        return maxOf(l, r, rest) > n / 2
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:
        self.l = self.r = 0
        def dfs(node: TreeNode) -> int:
            if not node:
                return 0
            left = dfs(node.left)
            right = dfs(node.right)
            if node.val == x:
                self.l, self.r = left, right
            return left + right + 1
        dfs(root)
        rest = n - (self.l + self.r + 1)
        return max(self.l, self.r, rest) > n // 2
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// Definition for a binary tree node.
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}
impl Solution {
    pub fn btree_game_winning_move(root: Option<Box<TreeNode>>, n: i32, x: i32) -> bool {
        fn dfs(node: &Option<Box<TreeNode>>, x: i32, l: &mut i32, r: &mut i32) -> i32 {
            if let Some(node) = node {
                let left = dfs(&node.left, x, l, r);
                let right = dfs(&node.right, x, l, r);
                if node.val == x {
                    *l = left;
                    *r = right;
                }
                left + right + 1
            } else {
                0
            }
        }
        let (mut l, mut r) = (0, 0);
        dfs(&root, x, &mut l, &mut r);
        let rest = n - (l + r + 1);
        l.max(r).max(rest) > n / 2
    }
}

Complexity

  • ⏰ Time complexity: O(n) — Each node is visited once.
  • 🧺 Space complexity: O(h) — h is the height of the tree (recursion stack).