Problem#
Given the root of a binary tree, return the level order traversal of its nodes’ values . (i.e., from left to right, level by level).
NOTE : This problem is very similar to - Create linked lists of all the nodes at each depth for a Binary Tree
Examples#
Example 1#
1
2
3
4
5
3
/ \
9 20
/ \
15 7
1
2
Input: root = [ 3 , 9 , 20 , null , null , 15 , 7 ]
Output:[[ 3 ], [ 9 , 20 ], [ 15 , 7 ]]
Solution#
Method 1 - Naive Approach#
Here is the logic:
Get the height of the tree.
Put a for loop for each level in tree.
for each level in step 2, do pre order traversal and print only when height matches to the level.
Look at the code for better explanation
Code#
Java
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public List< List< Integer>> levelOrder (TreeNode root) {
int h = height(root);
List< List< Integer>> ans = new LinkedList<> ();
for (int i = 1; i <= h; i++ ) {
List< Integer> currLevel = new LinkedList<> ();
printLevels(root, i, currLevel);
ans.add (currLevel);
}
return ans;
}
public void printLevels (TreeNode root, int h, List< Integer> currLevel) {
if (root == null ) {
return ;
}
if (h == 1) {
currLevel.add (root.val );
}
else {
printLevels(root.left , h - 1, currLevel);
printLevels(root.right , h - 1, currLevel);
}
}
public int height (TreeNode root) {
if (root == null ) {
return 0;
}
return 1 + Math.max (height(root.left ), height(root.right ));
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution :
def levelOrder (self, root):
def height (node):
if not node:
return 0
return 1 + max(height(node. left), height(node. right))
def printLevels (node, h, currLevel):
if not node:
return
if h == 1 :
currLevel. append(node. val)
else :
printLevels(node. left, h - 1 , currLevel)
printLevels(node. right, h - 1 , currLevel)
h = height(root)
ans = []
for i in range(1 , h + 1 ):
currLevel = []
printLevels(root, i, currLevel)
ans. append(currLevel)
return ans
Complexity#
⏰ Time Complexity: O(N^2) — For each level, you traverse the entire tree, resulting in quadratic time for a tree with N nodes.
🧺 Space Complexity: O(N) — The recursion stack can go as deep as the height of the tree, and the result list stores all node values.
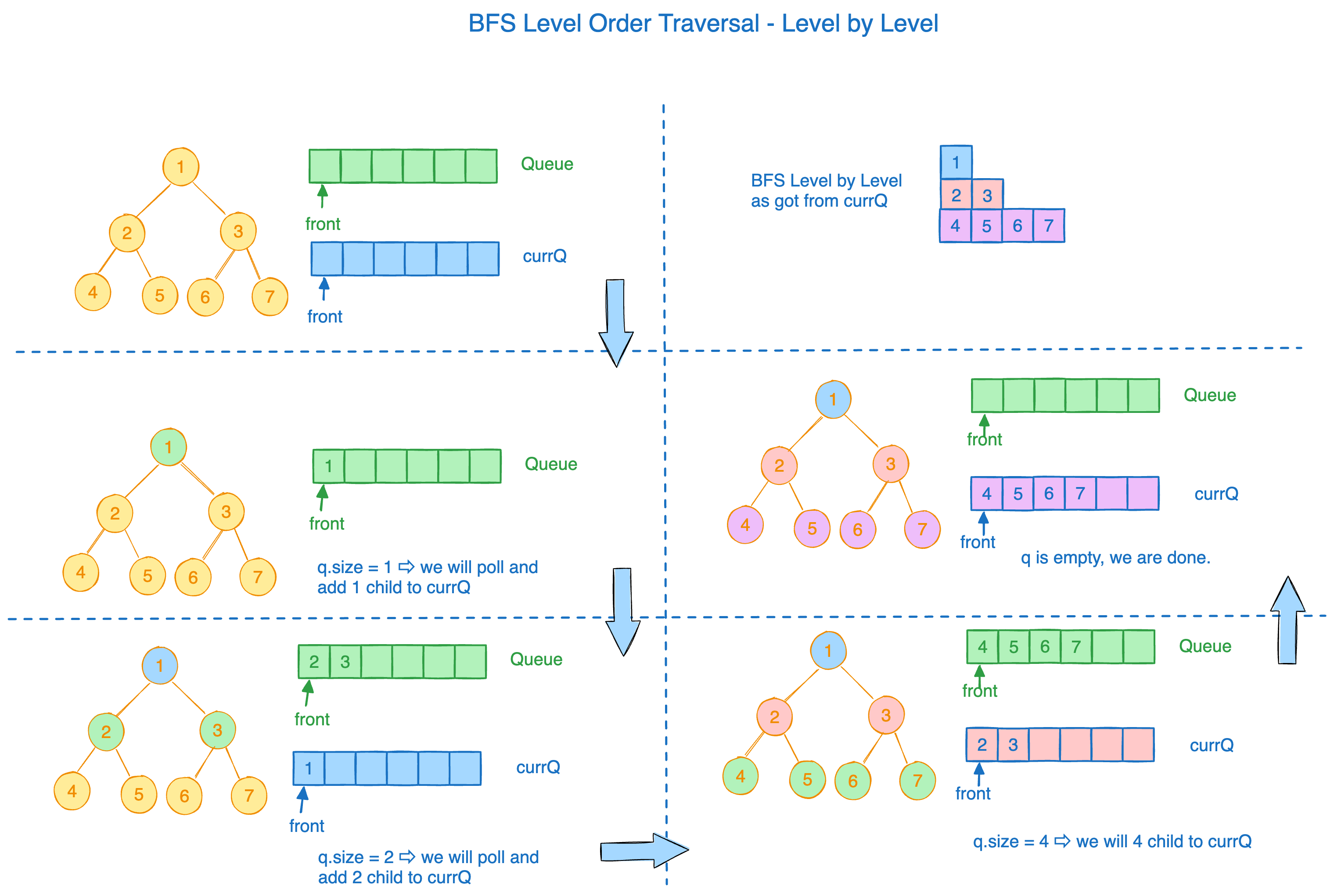
Method 2 - Using Queue and Size of Queue 🏆#
Create a ArrayList of Linked List Nodes.
Do the level order traversal using queue(Breadth First Search) - Binary Tree Level Order Traversal
For getting all the nodes at each level, before you take out a node from queue, store the size of the queue in a variable, say you call it as queueSize.
Now while queueSize>0, take out the nodes and print it and add their children into the queue.
After this while loop put a line break.
Dry Running of Above Code#
Note, in the diagram we are calling levelNodes = queueSize.
Since we had taken the queue size before we add new nodes, we will get the count at each level and after printing this count, put a line break, see the example below
Video explanation#
Here is the video explaining this method in detail. Please check it out:
VIDEO
Code#
Java
For More, Refer [Here](https://Stackoverflow.com/a/52051118/3222727).
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public List< List< Integer>> levelOrder (TreeNode root) {
List< List< Integer>> ans = new ArrayList<> ();
if (root == null ) {
return ans;
}
Queue< TreeNode> queue = new LinkedList<> ();
queue.offer (root);
while (! queue.isEmpty ()) {
List< Integer> currentLevel = new ArrayList<> ();
int queueSize = queue.size ();
for (int i = 0; i < queueSize; i++ ) {
TreeNode curr = queue.poll ();
currentLevel.add (curr.val );
if (curr.left != null ) {
queue.offer (curr.left );
}
if (curr.right != null ) {
queue.offer (curr.right );
}
}
ans.add (currentLevel);
}
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution :
def levelOrder (self, root: Optional[TreeNode]) -> List[List[int]]:
ans: List[List[int]] = []
if not root:
return ans
queue: deque[TreeNode] = deque([root])
while queue:
currentLevel: List[int] = []
queueSize: int = len(queue)
for _ in range(queueSize):
curr: TreeNode = queue. popleft()
currentLevel. append(curr. val)
if curr. left:
queue. append(curr. left)
if curr. right:
queue. append(curr. right)
ans. append(currentLevel)
return ans
Complexity#
⏰ Time complexity: O(n), where n is number of vertices as we go through all nodes
🧺 Space complexity: O(n) for storing elements in queues
Method 3 - Using 2 Queues#
It is obvious that this problem can be solve by using a queue. However, if we use one queue we can not track when each level starts. So we use two queues to track the current level and the next level.
Code#
Java
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public ArrayList< ArrayList< Integer>> levelOrder (TreeNode root) {
List< List< Integer>> ans = new ArrayList< ArrayList< Integer>> ();
if (root == null )
return ans;
List< Integer> nodeValues = new ArrayList<> ();
Queue< TreeNode> current = new LinkedList<> ();
Queue< TreeNode> next = new LinkedList<> ();
current.add (root);
while (! current.isEmpty ()){
TreeNode node = current.poll ();
if (node.left != null ) {
next.add (node.left );
}
if (node.right != null ) {
next.add (node.right );
}
nodeValues.add (node.val );
if (current.isEmpty ()){
current = next;
next = new LinkedList< TreeNode> ();
ans.add (nodeValues);
nodeValues = new ArrayList();
}
}
return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution :
def levelOrder (self, root):
if not root:
return []
ans = []
current = deque([root])
next_level = deque()
nodeValues = []
while current:
node = current. popleft()
if node. left:
next_level. append(node. left)
if node. right:
next_level. append(node. right)
nodeValues. append(node. val)
if not current:
ans. append(nodeValues)
current, next_level = next_level, deque()
nodeValues = []
return ans
Complexity#
Time Complexity – O(n) where n is number of vertices as we go through all nodes
Space Complexity - O(n) for storing elements in queues
Method 4 - DFS Recursive Approach#
I think that the recursive way of traversal is truly not recursive, it eventually relies on iterative steps over the height of the tree and the recursion can only be used in identifying the correct level and printing it.
Complexity#
⏰ Time complexity: O(n) — each node is visited exactly once in the DFS recursion and appended to its level list.
🧺 Space complexity: O(n) total. The output stores all node values O(n) and the recursion stack uses O(h) auxiliary space where h is the tree height (worst-case O(n) for a skewed tree).
Code#
Java
Python
As We Can See the for Loop Runs for O(h) Time Where H Is the Height of the Tree. Each of These H Calls to the Printcurrentlevel Routine Takes` O(h) * O(2k)` Time as in the Previous Iterative Way and the Same Justification Holds True for This Algorithm as Well.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public List< List< Integer>> levelOrder (TreeNode root) {
List< List< Integer>> levels = new ArrayList<> ();
if (root == null ) {
return levels;
}
helper(root, levels, 0);
return levels;
}
public void helper (TreeNode root, List< List< Integer>> ans, int level) {
if (root == null ) {
return ;
}
if (res.size () < level + 1) {
ans.add (new ArrayList<> ());
}
ans.get (level).add (root.val );
helper(root.left , ans, level + 1);
helper(root.right , ans, level + 1);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution :
def levelOrder (self, root):
levels = []
def helper (node, level):
if not node:
return
if len(levels) < level + 1 :
levels. append([])
levels[level]. append(node. val)
helper(node. left, level + 1 )
helper(node. right, level + 1 )
helper(root, 0 )
return levels
Summary#
This problem opens many possibilities to work with. For eg.
Populate next pointer to right node in Binary Tree Find level of a node, etc.