Binary Tree Longest Consecutive Sequence II

Problem

Given the root of a binary tree, return the length of the longest consecutive path in the tree.

A consecutive path is a path where the values of the consecutive nodes in the path differ by one. This path can be either increasing or decreasing.

For example, [1,2,3,4] and [4,3,2,1] are both considered valid, but the path [1,2,4,3] is not valid.

On the other hand, the path can be in the child-Parent-child order, where not necessarily be parent-child order.

Examples

Example 1:

1
2
3


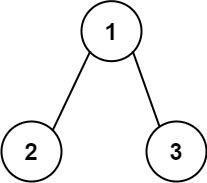
Input: root = [1,2,3]
Output: 2
Explanation: The longest consecutive path is [1, 2] or [2, 1].

Example 2:

1
2
3


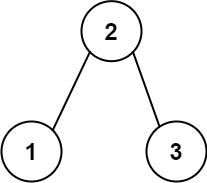
Input: root = [2,1,3]
Output: 3
Explanation: The longest consecutive path is [1, 2, 3] or [3, 2, 1].

Constraints:

The number of nodes in the tree is in the range [1, 3 * 10^4].
-3 * 10^4 <= Node.val <= 3 * 10^4

Solution

Method 1 – DFS with Up and Down Paths

Intuition

To find the longest consecutive path (increasing or decreasing by 1) in a binary tree, we use DFS to compute, for each node, the length of the longest increasing and decreasing paths passing through it. The answer is the maximum sum of up and down paths at any node minus 1 (since the node is counted twice).

Approach

Define a recursive DFS function that returns (inc, dec) for each node:
- inc: length of the longest increasing path starting at this node.
- dec: length of the longest decreasing path starting at this node.
For each child, if its value is one more or one less than the current node, update inc/dec accordingly.
At each node, update the global answer as inc + dec - 1.
Return the maximum answer found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    int ans = 0;
    pair<int,int> dfs(TreeNode* node) {
        if (!node) return {0,0};
        int inc = 1, dec = 1;
        if (node->left) {
            auto [linc, ldec] = dfs(node->left);
            if (node->val == node->left->val + 1) dec = ldec + 1;
            if (node->val == node->left->val - 1) inc = linc + 1;
        }
        if (node->right) {
            auto [rinc, rdec] = dfs(node->right);
            if (node->val == node->right->val + 1) dec = max(dec, rdec + 1);
            if (node->val == node->right->val - 1) inc = max(inc, rinc + 1);
        }
        ans = max(ans, inc + dec - 1);
        return {inc, dec};
    }
    int longestConsecutive(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func longestConsecutive(root *TreeNode) int {
    ans := 0
    var dfs func(*TreeNode) (int, int)
    dfs = func(node *TreeNode) (int, int) {
        if node == nil { return 0, 0 }
        inc, dec := 1, 1
        if node.Left != nil {
            linc, ldec := dfs(node.Left)
            if node.Val == node.Left.Val+1 { dec = ldec + 1 }
            if node.Val == node.Left.Val-1 { inc = linc + 1 }
        }
        if node.Right != nil {
            rinc, rdec := dfs(node.Right)
            if node.Val == node.Right.Val+1 { dec = max(dec, rdec+1) }
            if node.Val == node.Right.Val-1 { inc = max(inc, rinc+1) }
        }
        ans = max(ans, inc+dec-1)
        return inc, dec
    }
    dfs(root)
    return ans
}
func max(a, b int) int { if a > b { return a }; return b }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    int ans = 0;
    int[] dfs(TreeNode node) {
        if (node == null) return new int[]{0,0};
        int inc = 1, dec = 1;
        if (node.left != null) {
            int[] l = dfs(node.left);
            if (node.val == node.left.val + 1) dec = l[1] + 1;
            if (node.val == node.left.val - 1) inc = l[0] + 1;
        }
        if (node.right != null) {
            int[] r = dfs(node.right);
            if (node.val == node.right.val + 1) dec = Math.max(dec, r[1] + 1);
            if (node.val == node.right.val - 1) inc = Math.max(inc, r[0] + 1);
        }
        ans = Math.max(ans, inc + dec - 1);
        return new int[]{inc, dec};
    }
    public int longestConsecutive(TreeNode root) {
        dfs(root);
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    var ans = 0
    fun dfs(node: TreeNode?): Pair<Int, Int> {
        if (node == null) return 0 to 0
        var inc = 1
        var dec = 1
        node.left?.let {
            val (linc, ldec) = dfs(it)
            if (node.`val` == it.`val` + 1) dec = ldec + 1
            if (node.`val` == it.`val` - 1) inc = linc + 1
        }
        node.right?.let {
            val (rinc, rdec) = dfs(it)
            if (node.`val` == it.`val` + 1) dec = maxOf(dec, rdec + 1)
            if (node.`val` == it.`val` - 1) inc = maxOf(inc, rinc + 1)
        }
        ans = maxOf(ans, inc + dec - 1)
        return inc to dec
    }
    fun longestConsecutive(root: TreeNode?): Int {
        dfs(root)
        return ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def longestConsecutive(self, root: TreeNode) -> int:
        self.ans = 0
        def dfs(node: TreeNode) -> tuple[int, int]:
            if not node:
                return 0, 0
            inc, dec = 1, 1
            if node.left:
                linc, ldec = dfs(node.left)
                if node.val == node.left.val + 1:
                    dec = ldec + 1
                if node.val == node.left.val - 1:
                    inc = linc + 1
            if node.right:
                rinc, rdec = dfs(node.right)
                if node.val == node.right.val + 1:
                    dec = max(dec, rdec + 1)
                if node.val == node.right.val - 1:
                    inc = max(inc, rinc + 1)
            self.ans = max(self.ans, inc + dec - 1)
            return inc, dec
        dfs(root)
        return self.ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


// Definition for a binary tree node.
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}
impl Solution {
    pub fn longest_consecutive(root: Option<Box<TreeNode>>) -> i32 {
        fn dfs(node: &Option<Box<TreeNode>>, ans: &mut i32) -> (i32, i32) {
            if let Some(node) = node {
                let (linc, ldec) = dfs(&node.left, ans);
                let (rinc, rdec) = dfs(&node.right, ans);
                let mut inc = 1;
                let mut dec = 1;
                if let Some(left) = &node.left {
                    if node.val == left.val + 1 { dec = ldec + 1; }
                    if node.val == left.val - 1 { inc = linc + 1; }
                }
                if let Some(right) = &node.right {
                    if node.val == right.val + 1 { dec = dec.max(rdec + 1); }
                    if node.val == right.val - 1 { inc = inc.max(rinc + 1); }
                }
                *ans = (*ans).max(inc + dec - 1);
                (inc, dec)
            } else {
                (0, 0)
            }
        }
        let mut ans = 0;
        dfs(&root, &mut ans);
        ans
    }
}

Complexity

⏰ Time complexity: O(n) — Each node is visited once.
🧺 Space complexity: O(h) — h is the height of the tree (recursion stack).

Problem#

Examples#

Solution#

Method 1 – DFS with Up and Down Paths#

Intuition#

Approach#

Code#

Complexity#