Binary Tree Path Sum - Maximum between any two leaves

Problem

Given a binary tree, find the maximum path sum from one leaf node to another.

Examples

Example 1

graph TD
    A(10)
    A --- B(2)
    A --- C(10)
    B(2) --- D(20)
    B(2) --- E(1)

    linkStyle 0 stroke:#FF0000,stroke-width:2px;
    linkStyle 1 stroke:#FF0000,stroke-width:2px;
    linkStyle 2 stroke:#FF0000,stroke-width:2px;

root = [10, 2, 10, 20, 1]
Output: 42
Explanation: The maximum path sum is obtained for the path 20 → 2 → 10 → 10. The sum of these values is 20 + 2 + 10 + 10 = 42.

Example 2

graph TD
    A("5") --- B(5) & C(6)
    B --- D("-8") & E(1)
    C --- F(3) & G(9)
    D --- H(2) & I(6)

linkStyle 4 stroke:#FF0000,stroke-width:2px;
linkStyle 5 stroke:#FF0000,stroke-width:2px;

root = [-15, 5, 6, -8, 1, 3, 9, 2, 6]
Output: 18
Explanation: The maximum path sum is obtained for the path 3 → 6 → 9. The sum of these values is 2 + (-8) + 5 + 6 + 9 = 27.

Solution

Method 1 - Recursive postorder traversal

To solve this problem:

• Key Observations:
  • The maximum path will either:
    • Lie completely within one subtree (left or right), or
    • Pass through the current node, combining contributions from both the left and right subtrees.
  • To compute this maximum, perform a post-order traversal, which allows us to evaluate the left and right subtrees first, then compute the combination at the current node.
• Goal: Maintain a global variable (max_sum in Python and maxSum in Java) to store the maximum path sum encountered so far, which may include contributions from both left and right subtrees via the root or stay entirely within one subtree.

Approach

1. Variable Setup:
   • Create a global variable max_sum (Python) or maxSum (Java) and initialise it to the smallest possible integer value (float('-inf') in Python or Integer.MIN_VALUE in Java). This will hold the maximum path sum encountered during traversal.
2. Post-order Traversal:
   • Traverse the tree in post-order: Starting from the root, process the left and right subtrees before evaluating the current node.
3. Local Computation at Each Node:
   • For each node:
     • Compute the maximum path sum for the left and right subtrees recursively.
     • If the current node has both left and right children, calculate a candidate path sum passing through the current node: candidate_sum = left_sum + right_sum + node.val
     • Update the global max_sum if candidate_sum exceeds the current max_sum.
     • Return the maximum path sum that can be extended upwards: return max(left_sum, right_sum) + node.val
4. Final Value:
   • At the end of the traversal, max_sum contains the maximum path sum from one leaf node to another.

Dry Run

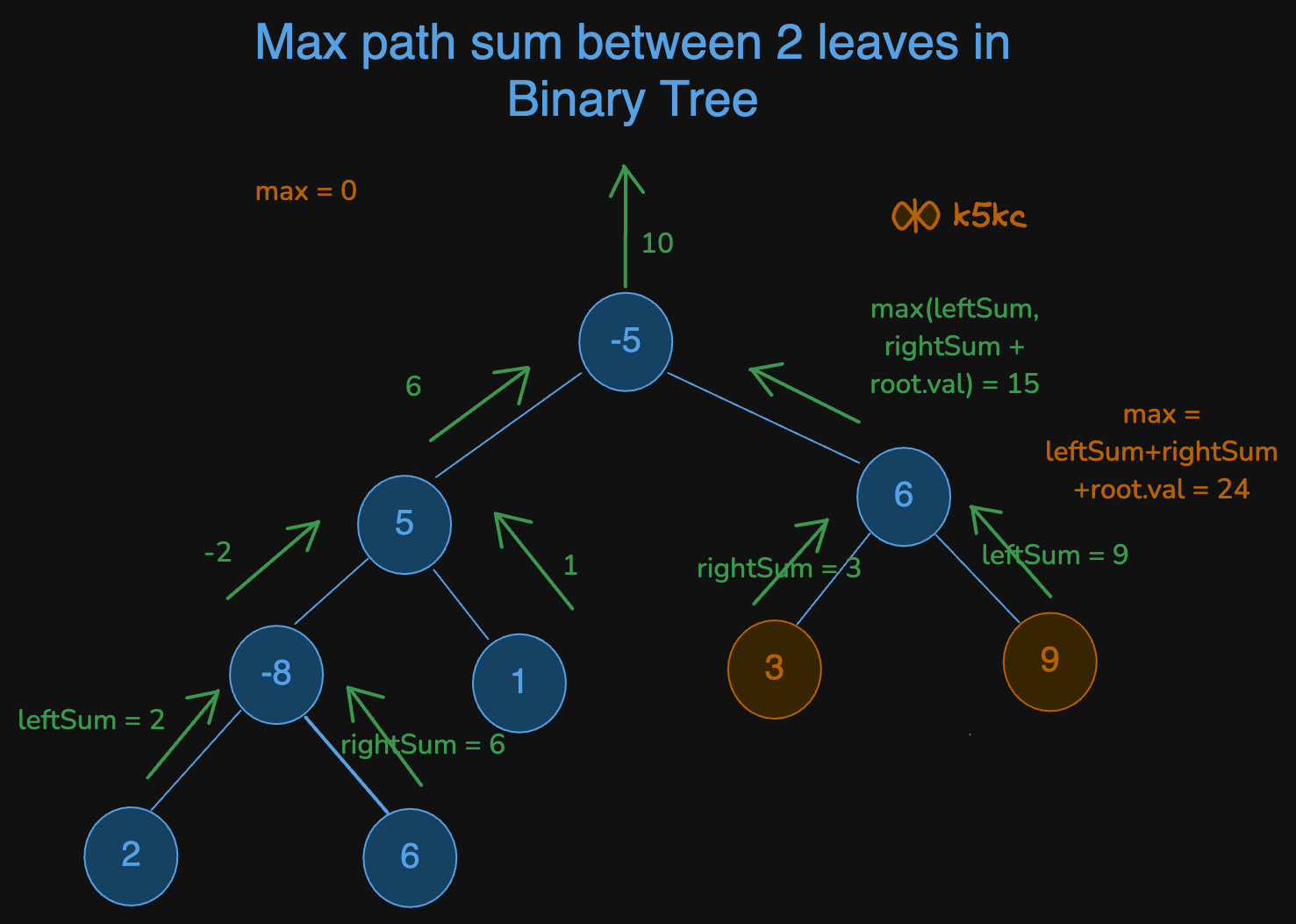
Code

Java

class Solution {
    private int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        // Helper function
        int helper(TreeNode node) {
            if (node == null) return 0;

            // If node is leaf, return its value
            if (node.left == null && node.right == null) return node.val;

            // Recursive calls for left and right subtrees
            int leftSum = node.left != null ? helper(node.left) : Integer.MIN_VALUE;
            int rightSum = node.right != null ? helper(node.right) : Integer.MIN_VALUE;

            // Update global maxSum for leaf-to-leaf path
            if (node.left != null && node.right != null) {
                maxSum = Math.max(maxSum, leftSum + rightSum + node.val);
            }

            // Return max path sum for this subtree
            return Math.max(leftSum, rightSum) + node.val;
        }

        helper(root);
        return maxSum != Integer.MIN_VALUE ? maxSum : root.val;
    }
}

Python

class Solution:
    def __init__(self):
        self.max_sum = float('-inf')

    # Function to calculate the maximum path sum from leaf to leaf
    def maxPathSum(self, root):
        def helper(node):
            if not node:
                return 0
            
            # If current node is a leaf node
            if not node.left and not node.right:
                return node.val
            
            # Recursive calls to left and right subtrees
            left_sum = helper(node.left) if node.left else float('-inf')
            right_sum = helper(node.right) if node.right else float('-inf')
            
            # Update the global maximum when left and right exist
            if node.left and node.right:
                self.max_sum = max(self.max_sum, left_sum + right_sum + node.val)
            
            # Return max path sum for the current node's subtree
            return max(left_sum, right_sum) + node.val
        
        helper(root)
        return self.max_sum if self.max_sum != float('-inf') else root.val

Complexity

• ⏰ Time complexity: O(n) since each node is visited once during traversal.
• 🧺 Space complexity: O(h) where h is the height of the binary tree due to the recursion stack.