Problem

Given the root of a binary tree, return the preorder traversal of its nodes’ values.

Examples

Example 1:

1
2
3
4
5

   1
    \
     2
    /
   3

1
2

Input: root = [1,null,2,3]
Output: [1,2,3]

Example 2:

graph TD;
1 --- 2 & 3
2 --- 4 & 5
3 --- 6 & 7
  
1
2

Input: root = [1,2,3,4,5, 6, 7]
Output: [1, 2, 4, 5, 3, 6, 7]

Solution

This is how the pre-order traversal looks:

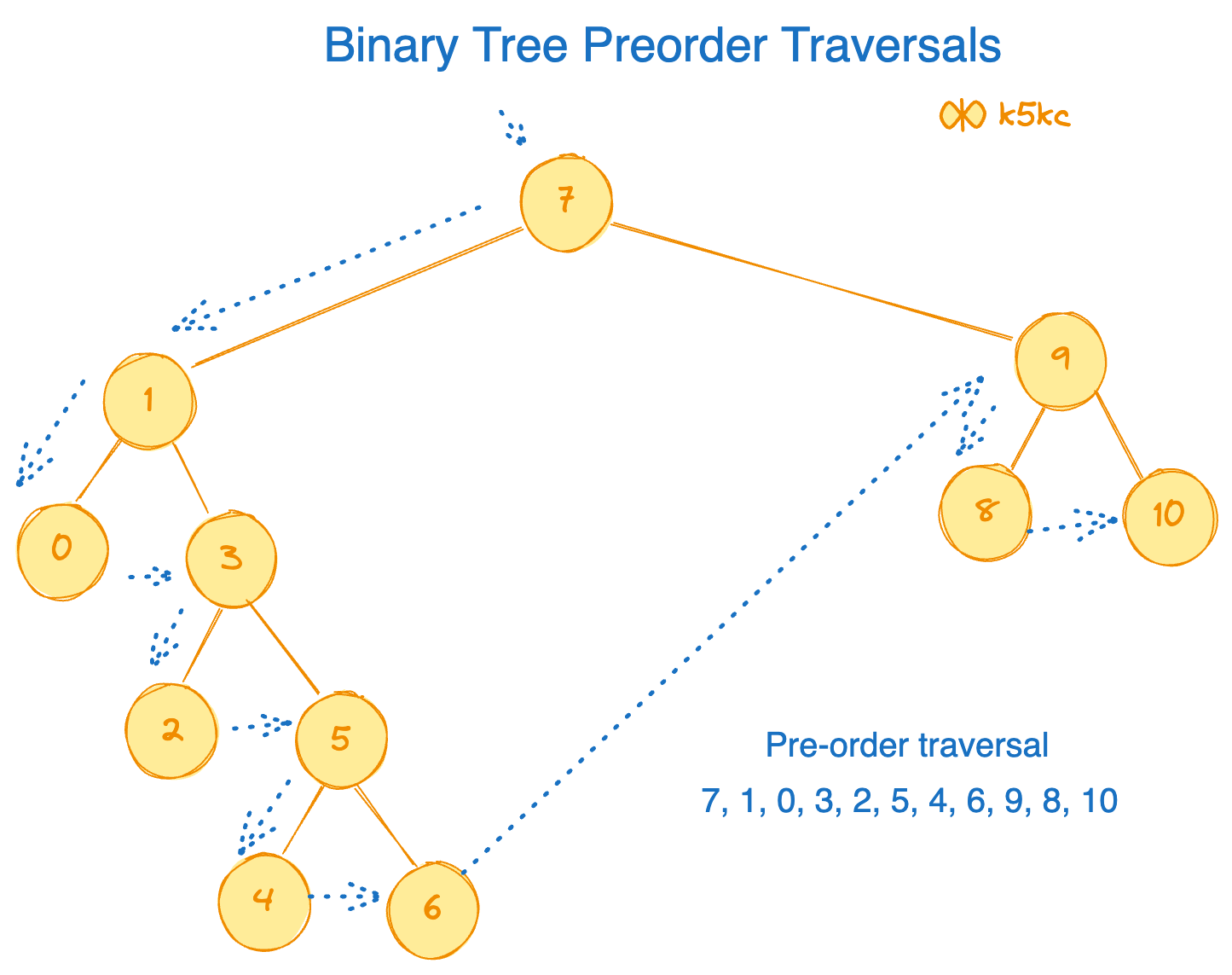
Method 1 - Recursive

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

public List<Integer> preorderTraversal(TreeNode root) {
	List<Integer> ans = new ArrayList<>();
	if (root == null) {
		return ans;
	}
	helper(root, ans);
}

private void helper(TreeNode root, List<Integer> ans) {
	if (root == null) {
		return;
	}
	ans.add(root.val);
	helper(root.left, ans);
	helper(root.right, ans);
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

pub fn preorder_traversal(root: NodeOpt) -> Vec<i32> {
	let mut result = vec![];
	Self::preorder_traversal_recurs(root, &mut result);
	result
}
fn preorder_traversal_recurs(root: NodeOpt, result: &mut Vec<i32>) {
	if let Some(pnode) = root {
		let node = pnode.borrow();
		result.push(node.val);
		Self::preorder_traversal_recurs(node.left.clone(), result);
		Self::preorder_traversal_recurs(node.right.clone(), result);
	}
}

Complexity

  • Time: O(N)
  • Space: O(1)

Method 2 - Iterative using stack

Algorithm

  1. Create a Stack.
  2. Push the root node to stack
  3. Start the loop, till stack is not empty
    1. Pop the element - add to pre-order traversal answer list
    2. Push the right child first (if exists)
    3. Push the left child second (if exists)
    4. Iterate on 3.1 - 3.3 till stack is not empty
  4. Return the traversal list

Note that we have pushed right child first, and then left child. This way we process left child first.

Dry Run

See below example to go through the algorithm above.

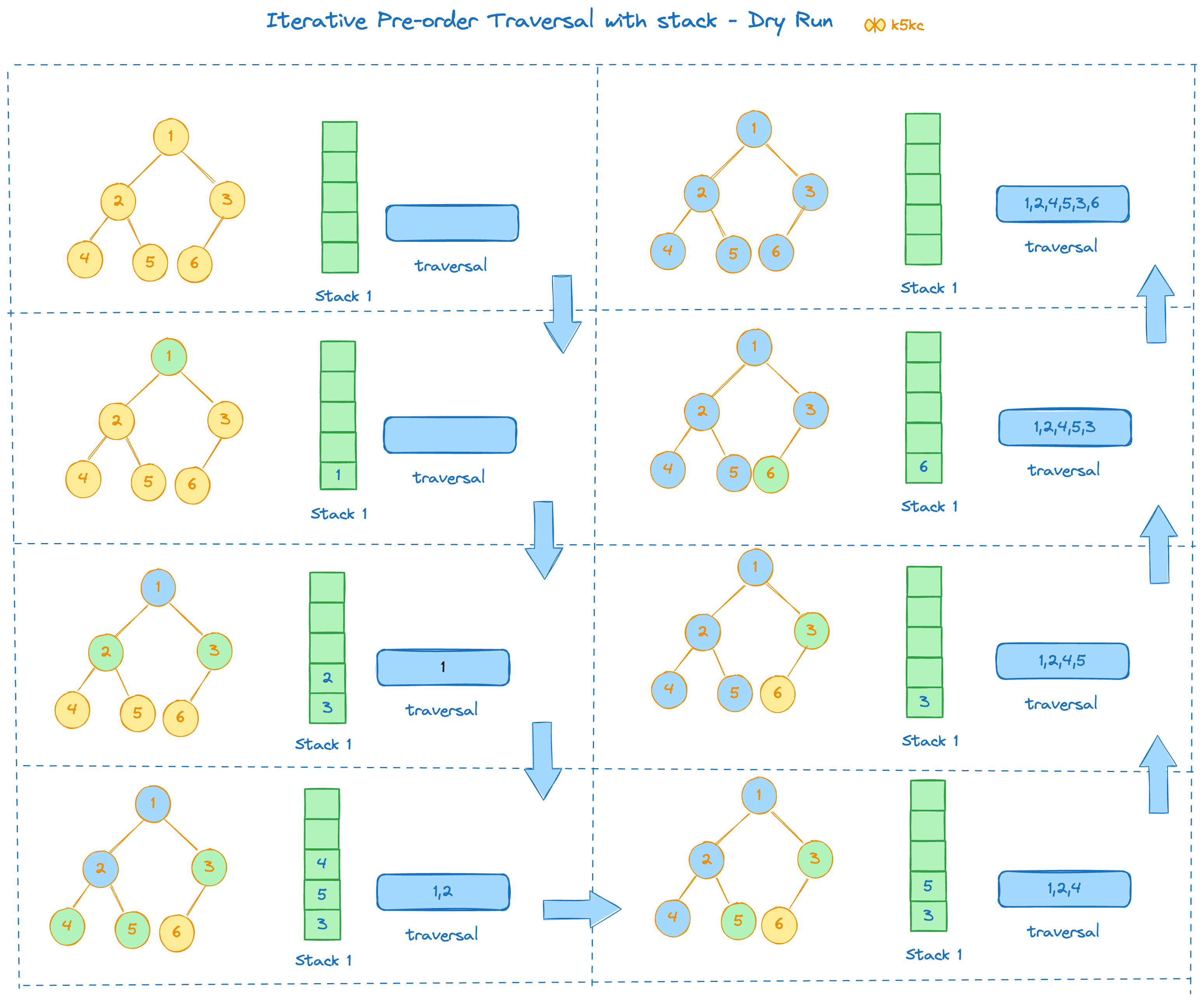
Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

public List<Integer> preorderTraversal(TreeNode root) {
	List<Integer> ans = new ArrayList<Integer>();
	if (root == null) {
		return ans;
	}
	Stack<TreeNode> stack = new Stack<TreeNode>();
	stack.push(root);
	while (!stack.isEmpty()){
		TreeNode node = stack.pop();
		ans.add(node.val);
		if (node.right != null) {
			stack.push(node.right);
		}
		if (node.left != null) {
			stack.push(node.left);
		}
	}
	return ans;
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

pub fn preorder_traversal(root: NodeOpt) -> Vec<i32> {
	Self::preorder_traversal_iter(root)
}
fn preorder_traversal_iter(root: NodeOpt) -> Vec<i32> {
	let mut result = vec![];
	let mut stack  = vec![root];
	while let Some(node_opt) = stack.pop() {
		if let Some(pnode) = node_opt {
			let node = pnode.borrow();
			result.push(node.val);
			stack.push(node.right.clone());
			stack.push(node.left.clone());
		}
	}
	result
}

Complexity

  • Time: O(n) where n is number of nodes in tree, as we go through all nodes
  • Space: O(n) - In worst case, stack can store all nodes in tree

Method 3 - Iterative using stack only for right children

We can do some optimization when storing the elements in stack. If we observe the code in method 2 carefully, we can process the current node without pushing it to the stack, and go to the left, and process next. There is only 1 problem, that we need to also process right child. So, how about keeping stack for right children.

See the code below.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

public List<Integer> preorderTraversal(TreeNode node) {
	List<Integer> ans = new LinkedList<Integer>();
	Stack<TreeNode> rights = new Stack<TreeNode>();
	while(node != null) {
		ans.add(node.val);
		if (node.right != null) {
			rights.push(node.right);
		}
		node = node.left;
		if (node == null && !rights.isEmpty()) {
			node = rights.pop();
		}
	}
    return ans;
}