problemeasyalgorithmsleetcode-563leetcode 563leetcode563

Binary Tree Tilt

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given the root of a binary tree, return the sum of every tree node 's tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

Examples

Example 1

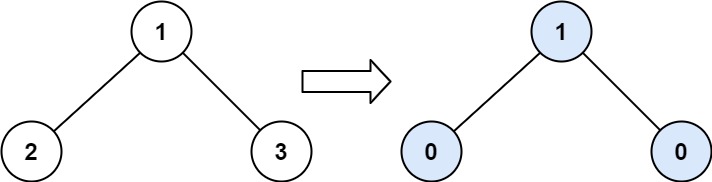
Input: root = [1,2,3]
Output: 1
Explanation: 
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

Example 2

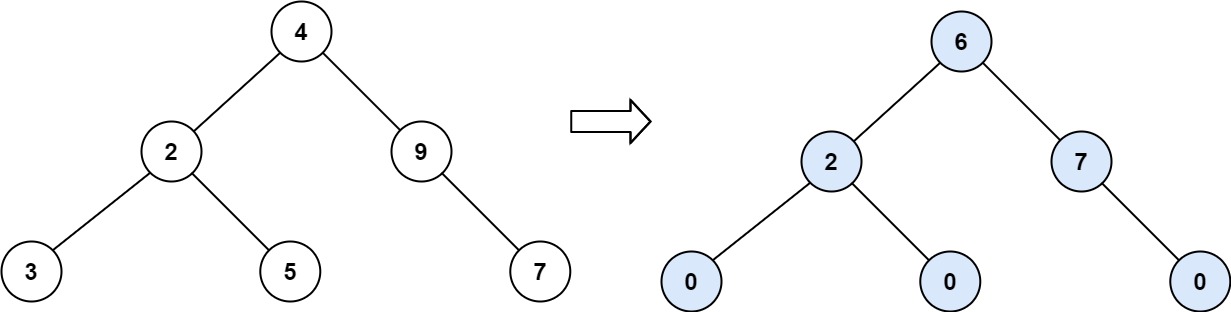
Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation: 
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3

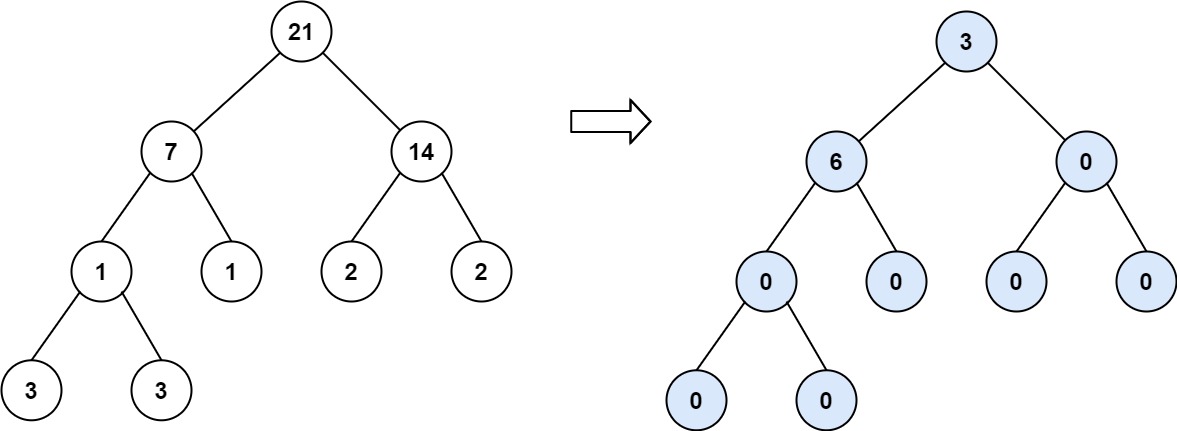
Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints

  • The number of nodes in the tree is in the range [0, 10^4].
  • -1000 <= Node.val <= 1000

Solution

Method 1 – Postorder DFS (Subtree Sums)

Intuition

To compute the tilt for each node, we need the sum of values in its left and right subtrees. A postorder DFS allows us to compute subtree sums and node tilts efficiently in one pass.

Approach

  1. Define a recursive DFS function that returns the sum of the subtree rooted at the current node.
  2. For each node, recursively compute the left and right subtree sums.
  3. The tilt at the node is the absolute difference between left and right subtree sums.
  4. Accumulate the tilt for all nodes in a variable.
  5. Return the total tilt after traversing the tree.

Code

C++
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    int ans = 0;
    int dfs(TreeNode* node) {
        if (!node) return 0;
        int l = dfs(node->left);
        int r = dfs(node->right);
        ans += abs(l - r);
        return l + r + node->val;
    }
    int findTilt(TreeNode* root) {
        dfs(root);
        return ans;
    }
};
Go
type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func findTilt(root *TreeNode) int {
    ans := 0
    var dfs func(*TreeNode) int
    dfs = func(node *TreeNode) int {
        if node == nil { return 0 }
        l := dfs(node.Left)
        r := dfs(node.Right)
        ans += abs(l - r)
        return l + r + node.Val
    }
    dfs(root)
    return ans
}
func abs(x int) int { if x < 0 { return -x }; return x }
Java
class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    int ans = 0;
    int dfs(TreeNode node) {
        if (node == null) return 0;
        int l = dfs(node.left);
        int r = dfs(node.right);
        ans += Math.abs(l - r);
        return l + r + node.val;
    }
    public int findTilt(TreeNode root) {
        dfs(root);
        return ans;
    }
}
Kotlin
data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    var ans = 0
    fun dfs(node: TreeNode?): Int {
        if (node == null) return 0
        val l = dfs(node.left)
        val r = dfs(node.right)
        ans += kotlin.math.abs(l - r)
        return l + r + node.`val`
    }
    fun findTilt(root: TreeNode?): Int {
        dfs(root)
        return ans
    }
}
Python
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def findTilt(self, root: TreeNode) -> int:
        self.ans = 0
        def dfs(node: TreeNode) -> int:
            if not node:
                return 0
            l = dfs(node.left)
            r = dfs(node.right)
            self.ans += abs(l - r)
            return l + r + node.val
        dfs(root)
        return self.ans
Rust
// Definition for a binary tree node.
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}
impl Solution {
    pub fn find_tilt(root: Option<Box<TreeNode>>) -> i32 {
        fn dfs(node: &Option<Box<TreeNode>>, ans: &mut i32) -> i32 {
            if let Some(node) = node {
                let l = dfs(&node.left, ans);
                let r = dfs(&node.right, ans);
                *ans += (l - r).abs();
                l + r + node.val
            } else {
                0
            }
        }
        let mut ans = 0;
        dfs(&root, &mut ans);
        ans
    }
}

Complexity

  • ⏰ Time complexity: O(n) — Each node is visited once.
  • 🧺 Space complexity: O(h) — h is the height of the tree (recursion stack).

Comments