Problem

Given a binary tree, return the top view of it.

What is Top View?

Top view means when you look the tree from the top the nodes you will see will be called the top view of the tree. See the example below.

Examples

Example 1:

1
2

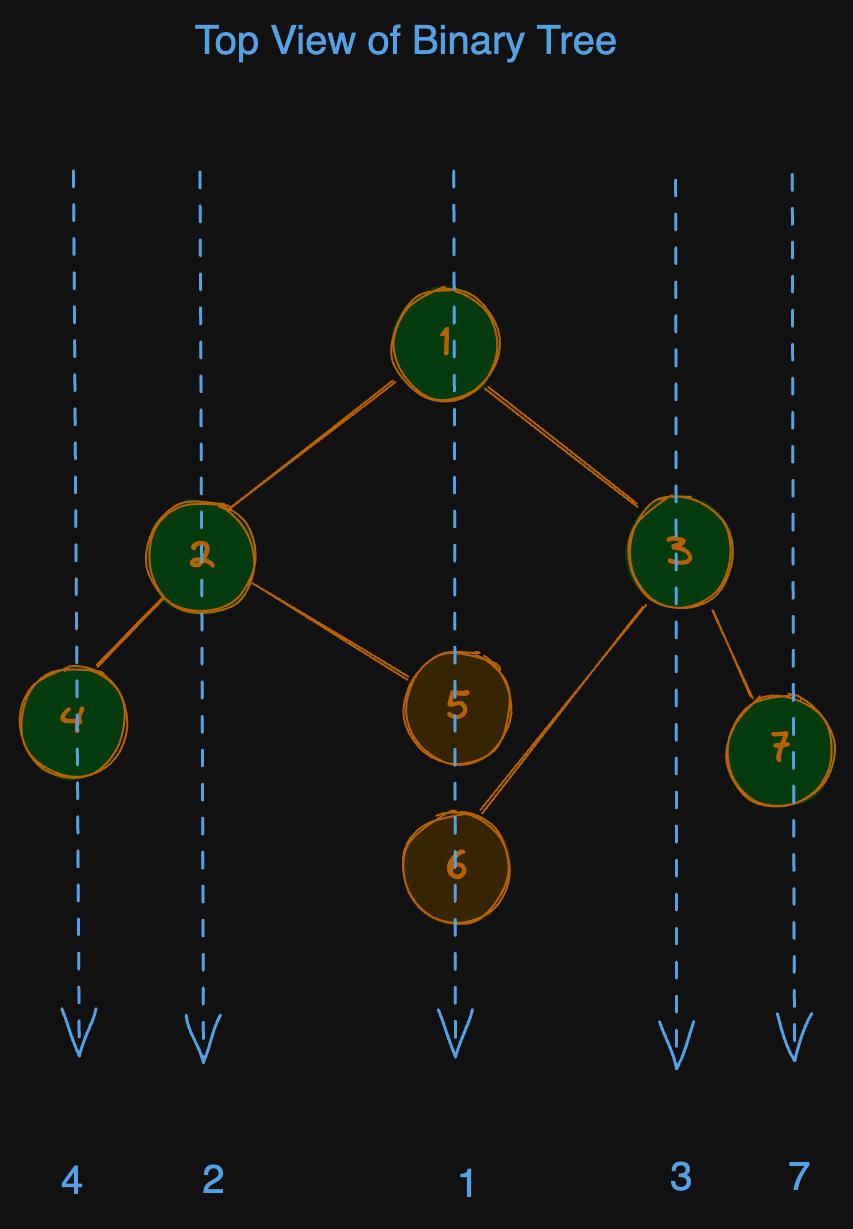
Input: root = [1,2,3,4,5,6,7]
Output: [4, 2, 1, 3, 7]

Solution

This Approach is quite similar to the – Binary Tree Traversal - Vertical Order Traversal.

Method 1 - Level Order Traversal

To capture the top view of a binary tree, we need to traverse the tree while keeping track of horizontal distances (HD) and levels. For each HD, we only keep the first node encountered. This can be efficiently achieved using a level order traversal (Breadth-First Search) and a dictionary to store the first node at each horizontal distance.

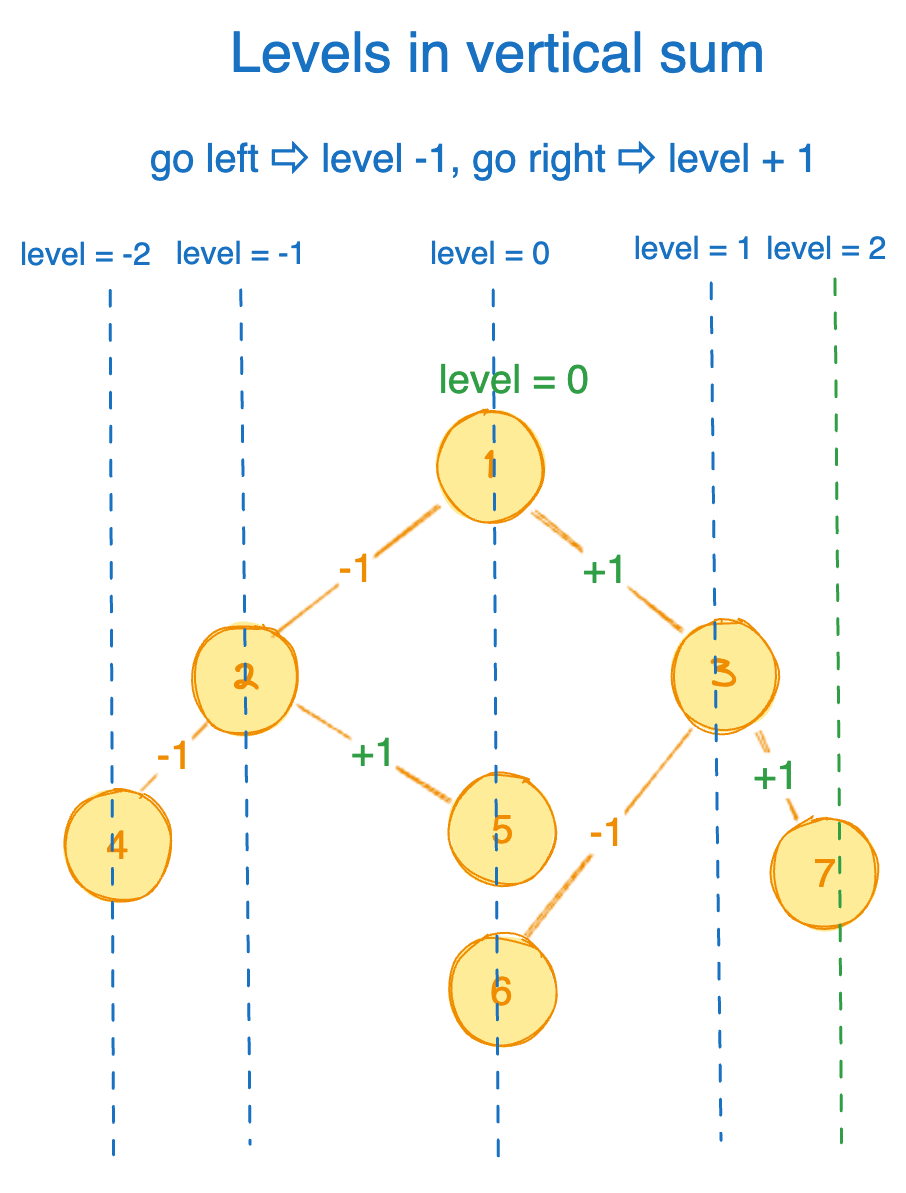
Approach

  1. Initialization: Start with initializing a queue and a dictionary (Map) where each key-value pair will be (horizontal distance, node value).
  2. Breadth-First Search: Implement a level order traversal (BFS) with a queue, keeping track of horizontal distances and levels.
  3. Track Nodes: For each horizontal distance, store only the first node encountered at that level.
  4. Result Extraction: After BFS traversal, sort the dictionary by horizontal distance and collect the values to form the top view.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    public List<Integer> topView(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }

        Map<Integer, Integer> hdNodeMap = new TreeMap<>();
        Queue<TreeNodeWithHd> queue = new LinkedList<>();
        queue.add(new TreeNodeWithHd(root, 0));

        while (!queue.isEmpty()) {
            TreeNodeWithHd nodeHd = queue.poll();
            TreeNode node = nodeHd.node;
            int hd = nodeHd.hd;

            if (!hdNodeMap.containsKey(hd)) {
                hdNodeMap.put(hd, node.val);
            }

            if (node.left != null) {
                queue.add(new TreeNodeWithHd(node.left, hd - 1));
            }

            if (node.right != null) {
                queue.add(new TreeNodeWithHd(node.right, hd + 1));
            }
        }

        for (Map.Entry<Integer, Integer> entry : hdNodeMap.entrySet()) {
            result.add(entry.getValue());
        }

        return result;
    }
}

class TreeNodeWithHd {
    TreeNode node;
    int hd;
    TreeNodeWithHd(TreeNode node, int hd) {
        this.node = node;
        this.hd = hd;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def topView(self, root: TreeNode) -> List[int]:
        if not root:
            return []

        hd_node_map: Dict[int, int] = {}
        queue: Deque[(TreeNode, int)] = deque([(root, 0)])

        while queue:
            node, hd = queue.popleft()

            if hd not in hd_node_map:
                hd_node_map[hd] = node.val

            if node.left:
                queue.append((node.left, hd - 1))
            
            if node.right:
                queue.append((node.right, hd + 1))
        
        return [hd_node_map[hd] for hd in sorted(hd_node_map)]

Complexity

  • ⏰ Time complexity: O(n) - where n is the number of nodes in the binary tree. Each node is visited once.
  • 🧺 Space complexity: O(n) - due to the storage of nodes in the queue and the dictionary.