Binary Tree Traversal - Vertical Order Traversal
Problem
Given a binary tree, return the vertical order traversal of its nodes' values. (ie, from top to bottom, column by column).
Examples
Example 1:
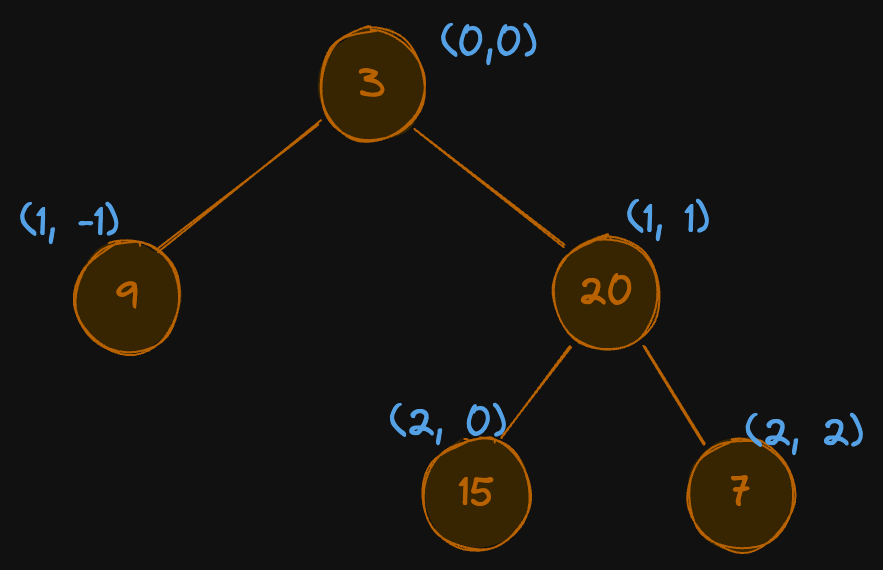
Input:
root = [3,9,20,null,null,15,7]
Output:
[[9],[3,15],[20],[7]]
Example 2:
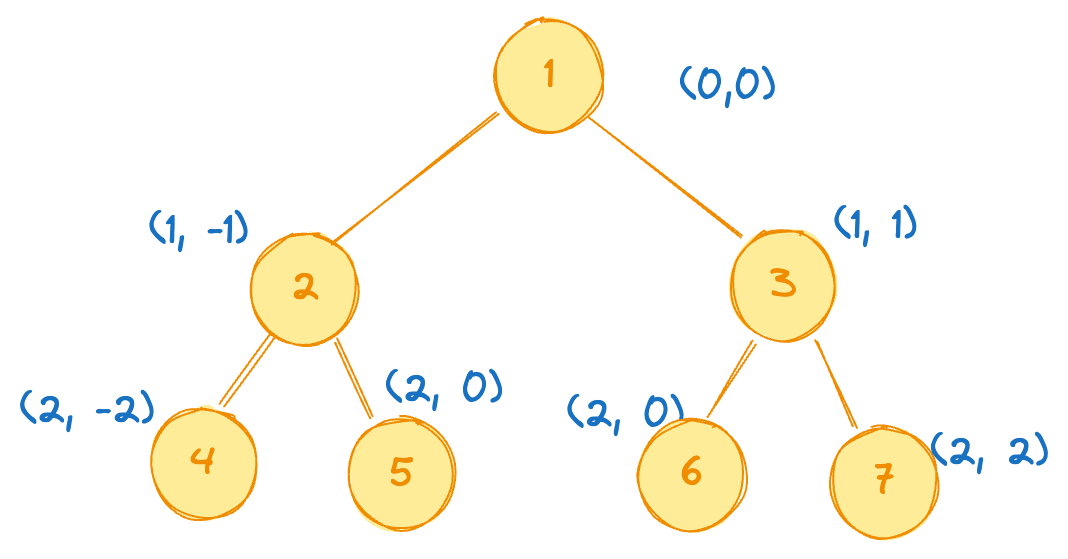
Input:
root = [1,2,3,4,5,6,7]
Output:
[[4],[2],[1,5,6],[3],[7]]
VS Similar Problem
Similar problem - [Vertical Order Traversal of a Binary Tree](vertical-order-traversal-of-a-binary-tree), which is leetcode 987.
This one is leetcode 314.
Difference between this solution and other one: 314. If two nodes are in the same row and column, the order should be from left to right. 987. If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.
Solution
We can clearly see that we are printing the nodes in vertical order such that a vertical line is scanning from left most node to right most node and printing all the nodes on the same vertical in a single line. How do we do it? Note that, the left most node will be printed first then its root then it’s right node. So, basically we are giving highest priority to left subtree, then root, and then lowest priority to right subtree. This gives us enough hint to solve this problem. How?
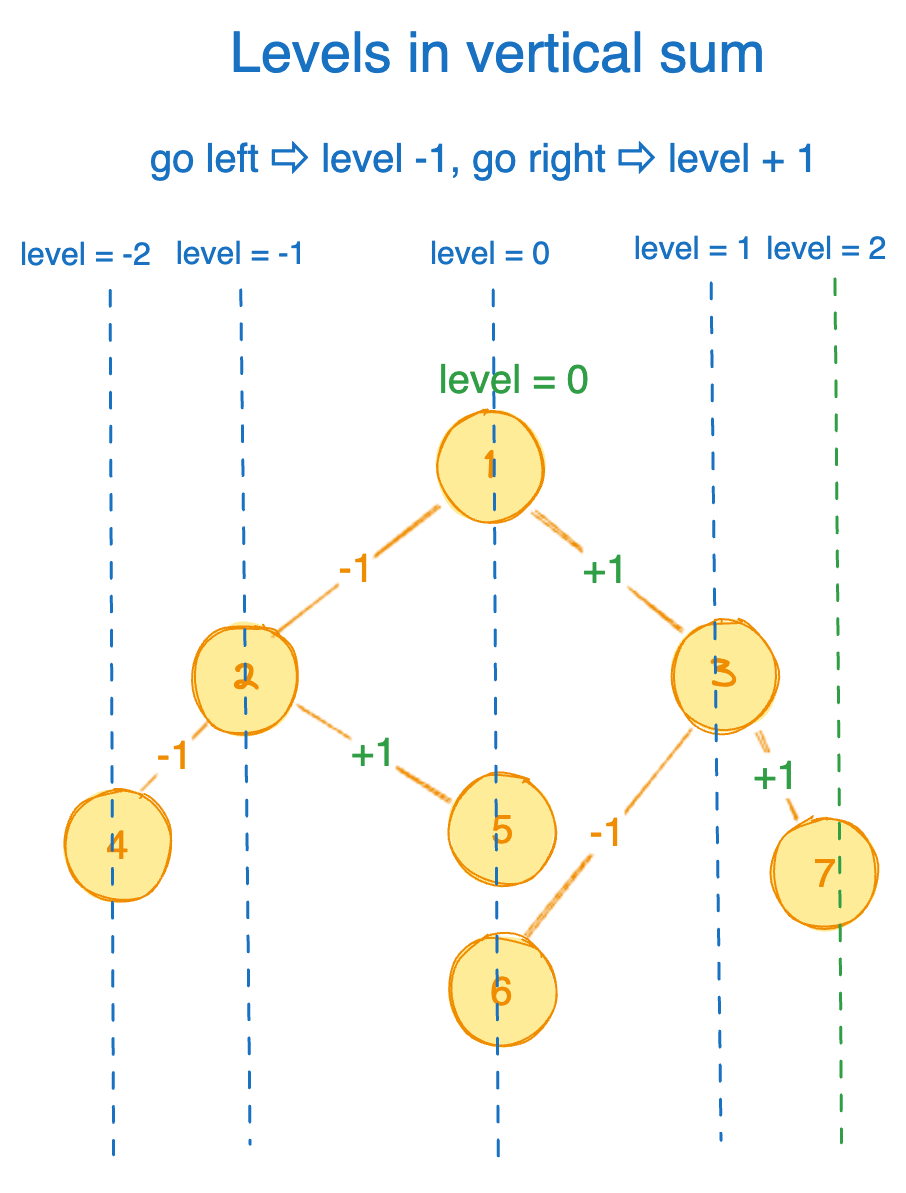
We will basically traverse the tree in pre-order (root -> left -> right) such a way that we assign one higher priority when we go left and one lower priority when we go right. Then we will basically put all the nodes with same priority value in a map. Once the traversal is done we can print the map nodes in the order of priority, sam priority nodes in the same line. For example, the following tree shows the assigned priority for each node in vertical traverse order lower value means higher priority.
For each node, its left child's degree is -1 and is right child's degree is +1. We can do a level order traversal and save the degree information.
1,0
/ \
2,-1 3,1
/ \ / \
4,-2 5,0 6,0 7,2
map :
-2 -> {4}
-1 -> {2}
0 -> {1, 5, 6}
1 -> {3}
2 -> {7}
Method 1 - Recursive Solution
Below is a simple implementation of this idea. We are passing minmax array to store the range of maps keys. In above example they are between [-2, 2].
public List<List<Integer>> verticalTraversal(TreeNode root) {
List<List<Integer>> ans = new ArrayList<List<Integer>> ();
Map<Integer, List<Integer>> verticals = new HashMap<>();
int[] minmax = new int[] {0, 0};
traverse(root, verticals, 0, new int[] {0, 0});
for (int i = minmax[0]; i <= minmax[1]; i++) {
if (verticals.containsKey(i)) {
ans.add(verticals.get(i));
}
}
return ans;
}
private void traverse(TreeNode node, Map <Integer, List<Integer>> verticals, int score, int[] minmax) {
verticals.putIfAbsent(score, new ArrayList<Integer>());
verticals.get(score).add(node.val);
minmax[0] = Math.min(minmax[0], score);
minmax[1] = Math.max(minmax[1], score);
if (node.left != null) {
traverse(node.left, verticals, score - 1, minmax);
}
if (node.right != null) {
traverse(node.right, verticals, score + 1, minmax);
}
}
Method 2 - Iterative
Here is another code:
public List<List<Integer>> verticalOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<List<Integer>> ();
if (root == null)
return result;
// level and list
Map<Integer, ArrayList<Integer>> map = new HashMap<> ();
LinkedList<TreeNode> queue = new LinkedList<TreeNode> ();
LinkedList<Integer> level = new LinkedList<Integer> ();
queue.offer(root);
level.offer(0);
int minLevel = 0;
int maxLevel = 0;
while (!queue.isEmpty()) {
TreeNode p = queue.poll();
int l = level.poll();
//track min and max levels
minLevel = Math.min(minLevel, l);
maxLevel = Math.max(maxLevel, l);
if (map.containsKey(l)) {
map.get(l).add(p.val);
} else {
ArrayList<Integer> list = new ArrayList<Integer> ();
list.add(p.val);
map.put(l, list);
}
if (p.left != null) {
queue.offer(p.left);
level.offer(l - 1);
}
if (p.right != null) {
queue.offer(p.right);
level.offer(l + 1);
}
}
for (int i = minLevel; i<= maxLevel; i++) {
if (map.containsKey(i)) {
result.add(map.get(i));
}
}
return result;
}