problemhardalgorithmsleetcode-3161leetcode 3161leetcode3161

Block Placement Queries

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There exists an infinite number line, with its origin at 0 and extending towards the positive x-axis.

You are given a 2D array queries, which contains two types of queries:

  1. For a query of type 1, queries[i] = [1, x]. Build an obstacle at distance x from the origin. It is guaranteed that there is no obstacle at distance x when the query is asked.
  2. For a query of type 2, queries[i] = [2, x, sz]. Check if it is possible to place a block of size sz anywhere in the range [0, x] on the line, such that the block entirely lies in the range [0, x]. A block cannot be placed if it intersects with any obstacle, but it may touch it. Note that you donot actually place the block. Queries are separate.

Return a boolean array results, where results[i] is true if you can place the block specified in the ith query of type 2, and false otherwise.

Examples

Example 1

Input: queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]
Output: [false,true,true]
Explanation:

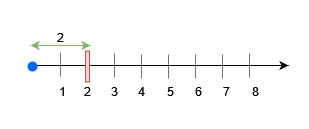For query 0, place an obstacle at x = 2. A block of size at most 2 can be placed before x = 3.

Example 2

Input: queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]
Output: [true,true,false]
Explanation:

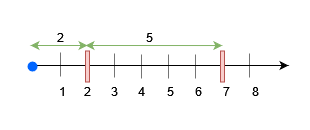
  • Place an obstacle at x = 7 for query 0. A block of size at most 7 can be placed before x = 7.
  • Place an obstacle at x = 2 for query 2. Now, a block of size at most 5 can be placed before x = 7, and a block of size at most 2 before x = 2.

Constraints

  • 1 <= queries.length <= 15 * 10^4
  • 2 <= queries[i].length <= 3
  • 1 <= queries[i][0] <= 2
  • 1 <= x, sz <= min(5 * 104, 3 * queries.length)
  • The input is generated such that for queries of type 1, no obstacle exists at distance x when the query is asked.
  • The input is generated such that there is at least one query of type 2.

Solution

Method 1 – Ordered Set (Binary Search Tree)

Intuition

To efficiently insert obstacles and answer range queries, we maintain a sorted set of obstacle positions. For each type 2 query, we check all intervals between obstacles (including 0 and x as boundaries) to see if any interval can fit the block.

Approach

  1. Use a balanced BST or ordered set to store obstacle positions.
  2. For each query:
    • If type 1, insert x into the set.
    • If type 2, find all obstacles in [0, x] and check the gaps between consecutive obstacles (including 0 and x as boundaries).
    • For each gap, if the interval is at least sz, return true for this query.
  3. Collect results for all type 2 queries.

Code

C++
#include <set>
class Solution {
public:
    vector<bool> blockPlacementQueries(vector<vector<int>>& queries) {
        set<long long> obs;
        vector<bool> ans;
        for (auto& q : queries) {
            if (q[0] == 1) {
                obs.insert(q[1]);
            } else {
                long long x = q[1], sz = q[2];
                obs.insert(-1); obs.insert(x+1);
                auto it = obs.lower_bound(0);
                long long prev = -1;
                bool ok = false;
                while (it != obs.end() && *it <= x+1) {
                    if (*it - prev - 1 >= sz) ok = true;
                    prev = *it;
                    ++it;
                }
                obs.erase(-1); obs.erase(x+1);
                ans.push_back(ok);
            }
        }
        return ans;
    }
};
Go
func blockPlacementQueries(queries [][]int) []bool {
    import "sort"
    obs := []int{}
    ans := []bool{}
    for _, q := range queries {
        if q[0] == 1 {
            obs = append(obs, q[1])
        } else {
            x, sz := q[1], q[2]
            tmp := append(obs[:], 0, x+1)
            sort.Ints(tmp)
            ok := false
            for i := 1; i < len(tmp); i++ {
                if tmp[i]-tmp[i-1]-1 >= sz {
                    ok = true
                    break
                }
            }
            ans = append(ans, ok)
        }
    }
    return ans
}
Java
import java.util.*;
class Solution {
    public List<Boolean> blockPlacementQueries(int[][] queries) {
        TreeSet<Integer> obs = new TreeSet<>();
        List<Boolean> ans = new ArrayList<>();
        for (int[] q : queries) {
            if (q[0] == 1) {
                obs.add(q[1]);
            } else {
                int x = q[1], sz = q[2];
                obs.add(-1); obs.add(x+1);
                Integer prev = -1;
                for (Integer pos : obs.tailSet(0)) {
                    if (pos > x+1) break;
                    if (pos - prev - 1 >= sz) {
                        ans.add(true);
                        break;
                    }
                    prev = pos;
                }
                if (ans.size() < queries.length && (ans.isEmpty() || !ans.get(ans.size()-1))) ans.add(false);
                obs.remove(-1); obs.remove(x+1);
            }
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun blockPlacementQueries(queries: Array<IntArray>): List<Boolean> {
        val obs = sortedSetOf<Int>()
        val ans = mutableListOf<Boolean>()
        for (q in queries) {
            if (q[0] == 1) {
                obs.add(q[1])
            } else {
                val x = q[1]
                val sz = q[2]
                obs.add(-1); obs.add(x+1)
                var prev = -1
                var ok = false
                for (pos in obs.tailSet(0)) {
                    if (pos > x+1) break
                    if (pos - prev - 1 >= sz) ok = true
                    prev = pos
                }
                obs.remove(-1); obs.remove(x+1)
                ans.add(ok)
            }
        }
        return ans
    }
}
Python
class Solution:
    def blockPlacementQueries(self, queries: list[list[int]]) -> list[bool]:
        import bisect
        obs = []
        ans = []
        for q in queries:
            if q[0] == 1:
                bisect.insort(obs, q[1])
            else:
                x, sz = q[1], q[2]
                tmp = [0] + obs + [x+1]
                tmp = [p for p in tmp if p <= x+1]
                ok = False
                for i in range(1, len(tmp)):
                    if tmp[i] - tmp[i-1] - 1 >= sz:
                        ok = True
                        break
                ans.append(ok)
        return ans
Rust
impl Solution {
    pub fn block_placement_queries(queries: Vec<Vec<i32>>) -> Vec<bool> {
        let mut obs = vec![];
        let mut ans = vec![];
        for q in queries {
            if q[0] == 1 {
                obs.push(q[1]);
                obs.sort();
            } else {
                let x = q[1];
                let sz = q[2];
                let mut tmp = vec![0];
                tmp.extend(&obs);
                tmp.push(x+1);
                tmp.retain(|&p| p <= x+1);
                let mut ok = false;
                for i in 1..tmp.len() {
                    if tmp[i] - tmp[i-1] - 1 >= sz {
                        ok = true;
                        break;
                    }
                }
                ans.push(ok);
            }
        }
        ans
    }
}

Complexity

  • ⏰ Time complexity: O(q log q) per query due to sorting/insertions.
  • 🧺 Space complexity: O(q) — For storing obstacles.

Comments