Boundary of Binary Tree

Problem

The boundary of a binary tree is the concatenation of the root , the left boundary , the leaves ordered from left-to-right, and the reverse order of the right boundary.

The left boundary is the set of nodes defined by the following:

The root node’s left child is in the left boundary. If the root does not have a left child, then the left boundary is empty.
If a node in the left boundary and has a left child, then the left child is in the left boundary.
If a node is in the left boundary, has no left child, but has a right child, then the right child is in the left boundary.
The leftmost leaf is not in the left boundary.

The right boundary is similar to the left boundary , except it is the right side of the root’s right subtree. Again, the leaf is not part of the right boundary , and the right boundary is empty if the root does not have a right child.

The leaves are nodes that do not have any children. For this problem, the root is not a leaf.

Given the root of a binary tree, return the values of itsboundary.

Examples

Example 1:

1
2
3
4
5
6
7
8


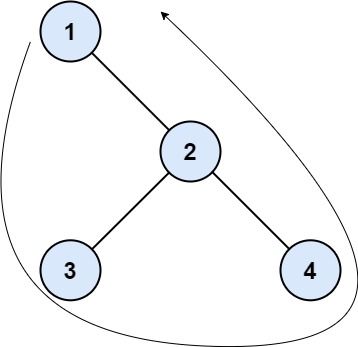
Input: root = [1,null,2,3,4]
Output: [1,3,4,2]
Explanation:
- The left boundary is empty because the root does not have a left child.
- The right boundary follows the path starting from the root's right child 2 -> 4.
  4 is a leaf, so the right boundary is [2].
- The leaves from left to right are [3,4].
Concatenating everything results in [1] + [] + [3,4] + [2] = [1,3,4,2].

Example 2:

1
2
3
4
5
6
7
8
9


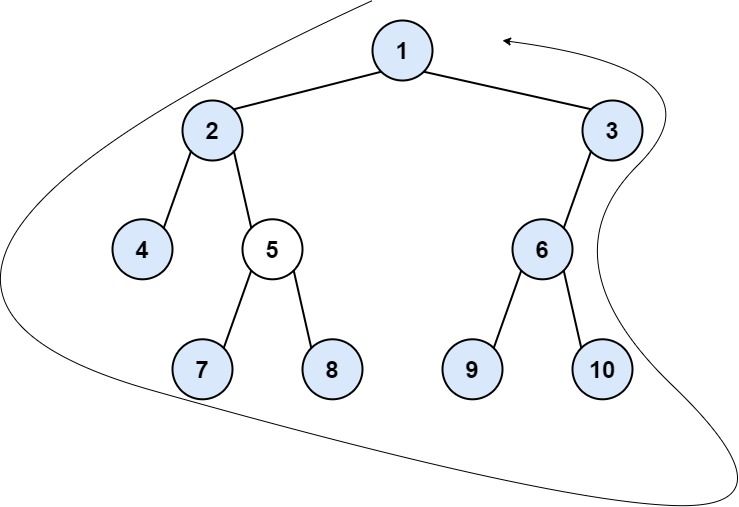
Input: root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
Output: [1,2,4,7,8,9,10,6,3]
Explanation:
- The left boundary follows the path starting from the root's left child 2 -> 4.
  4 is a leaf, so the left boundary is [2].
- The right boundary follows the path starting from the root's right child 3 -> 6 -> 10.
  10 is a leaf, so the right boundary is [3,6], and in reverse order is [6,3].
- The leaves from left to right are [4,7,8,9,10].
Concatenating everything results in [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3].

Constraints:

The number of nodes in the tree is in the range [1, 10^4].
-1000 <= Node.val <= 1000

Solution

Method 1 – DFS for Left Boundary, Leaves, and Right Boundary

Intuition

The boundary of a binary tree can be constructed by traversing the left boundary, collecting all leaves, and then traversing the right boundary in reverse. We use DFS to collect each part, taking care to avoid duplicates.

Approach

If the tree is empty, return an empty list.
Add the root value to the answer.
Traverse the left boundary (excluding leaves and root) using DFS.
Traverse all leaves (excluding those already in the boundary) using DFS.
Traverse the right boundary (excluding leaves and root) using DFS, and add them in reverse order.
Return the concatenated result.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    void leftBoundary(TreeNode* node, vector<int>& ans) {
        if (!node || (!node->left && !node->right)) return;
        ans.push_back(node->val);
        if (node->left) leftBoundary(node->left, ans);
        else leftBoundary(node->right, ans);
    }
    void rightBoundary(TreeNode* node, vector<int>& ans) {
        if (!node || (!node->left && !node->right)) return;
        if (node->right) rightBoundary(node->right, ans);
        else rightBoundary(node->left, ans);
        ans.push_back(node->val);
    }
    void leaves(TreeNode* node, vector<int>& ans) {
        if (!node) return;
        if (!node->left && !node->right) ans.push_back(node->val);
        leaves(node->left, ans);
        leaves(node->right, ans);
    }
    vector<int> boundaryOfBinaryTree(TreeNode* root) {
        if (!root) return {};
        vector<int> ans;
        ans.push_back(root->val);
        leftBoundary(root->left, ans);
        leaves(root->left, ans);
        leaves(root->right, ans);
        vector<int> right;
        rightBoundary(root->right, right);
        ans.insert(ans.end(), right.rbegin(), right.rend());
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func boundaryOfBinaryTree(root *TreeNode) []int {
    if root == nil { return nil }
    ans := []int{root.Val}
    var leftBoundary func(*TreeNode)
    leftBoundary = func(node *TreeNode) {
        if node == nil || (node.Left == nil && node.Right == nil) { return }
        ans = append(ans, node.Val)
        if node.Left != nil { leftBoundary(node.Left) } else { leftBoundary(node.Right) }
    }
    var rightBoundary func(*TreeNode, *[]int)
    rightBoundary = func(node *TreeNode, right *[]int) {
        if node == nil || (node.Left == nil && node.Right == nil) { return }
        if node.Right != nil { rightBoundary(node.Right, right) } else { rightBoundary(node.Left, right) }
        *right = append(*right, node.Val)
    }
    var leaves func(*TreeNode)
    leaves = func(node *TreeNode) {
        if node == nil { return }
        if node.Left == nil && node.Right == nil { ans = append(ans, node.Val) }
        leaves(node.Left)
        leaves(node.Right)
    }
    leftBoundary(root.Left)
    leaves(root.Left)
    leaves(root.Right)
    right := []int{}
    rightBoundary(root.Right, &right)
    for i := len(right)-1; i >= 0; i-- { ans = append(ans, right[i]) }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    public List<Integer> boundaryOfBinaryTree(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        if (root == null) return ans;
        ans.add(root.val);
        leftBoundary(root.left, ans);
        leaves(root.left, ans);
        leaves(root.right, ans);
        List<Integer> right = new ArrayList<>();
        rightBoundary(root.right, right);
        for (int i = right.size()-1; i >= 0; --i) ans.add(right.get(i));
        return ans;
    }
    void leftBoundary(TreeNode node, List<Integer> ans) {
        if (node == null || (node.left == null && node.right == null)) return;
        ans.add(node.val);
        if (node.left != null) leftBoundary(node.left, ans);
        else leftBoundary(node.right, ans);
    }
    void rightBoundary(TreeNode node, List<Integer> ans) {
        if (node == null || (node.left == null && node.right == null)) return;
        if (node.right != null) rightBoundary(node.right, ans);
        else rightBoundary(node.left, ans);
        ans.add(node.val);
    }
    void leaves(TreeNode node, List<Integer> ans) {
        if (node == null) return;
        if (node.left == null && node.right == null) ans.add(node.val);
        leaves(node.left, ans);
        leaves(node.right, ans);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    fun boundaryOfBinaryTree(root: TreeNode?): List<Int> {
        if (root == null) return emptyList()
        val ans = mutableListOf<Int>()
        ans.add(root.`val`)
        fun leftBoundary(node: TreeNode?) {
            if (node == null || (node.left == null && node.right == null)) return
            ans.add(node.`val`)
            if (node.left != null) leftBoundary(node.left) else leftBoundary(node.right)
        }
        fun rightBoundary(node: TreeNode?, right: MutableList<Int>) {
            if (node == null || (node.left == null && node.right == null)) return
            if (node.right != null) rightBoundary(node.right, right) else rightBoundary(node.left, right)
            right.add(node.`val`)
        }
        fun leaves(node: TreeNode?) {
            if (node == null) return
            if (node.left == null && node.right == null) ans.add(node.`val`)
            leaves(node.left)
            leaves(node.right)
        }
        leftBoundary(root.left)
        leaves(root.left)
        leaves(root.right)
        val right = mutableListOf<Int>()
        rightBoundary(root.right, right)
        ans.addAll(right.reversed())
        return ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def boundaryOfBinaryTree(self, root: TreeNode) -> list[int]:
        if not root:
            return []
        ans = [root.val]
        def leftBoundary(node):
            if not node or (not node.left and not node.right):
                return
            ans.append(node.val)
            if node.left:
                leftBoundary(node.left)
            else:
                leftBoundary(node.right)
        def rightBoundary(node, right):
            if not node or (not node.left and not node.right):
                return
            if node.right:
                rightBoundary(node.right, right)
            else:
                rightBoundary(node.left, right)
            right.append(node.val)
        def leaves(node):
            if not node:
                return
            if not node.left and not node.right:
                ans.append(node.val)
            leaves(node.left)
            leaves(node.right)
        leftBoundary(root.left)
        leaves(root.left)
        leaves(root.right)
        right = []
        rightBoundary(root.right, right)
        ans += right[::-1]
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


// Definition for a binary tree node.
pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}
impl Solution {
    pub fn boundary_of_binary_tree(root: Option<Box<TreeNode>>) -> Vec<i32> {
        fn left_boundary(node: &Option<Box<TreeNode>>, ans: &mut Vec<i32>) {
            if let Some(node) = node {
                if node.left.is_none() && node.right.is_none() { return; }
                ans.push(node.val);
                if node.left.is_some() {
                    left_boundary(&node.left, ans);
                } else {
                    left_boundary(&node.right, ans);
                }
            }
        }
        fn right_boundary(node: &Option<Box<TreeNode>>, right: &mut Vec<i32>) {
            if let Some(node) = node {
                if node.left.is_none() && node.right.is_none() { return; }
                if node.right.is_some() {
                    right_boundary(&node.right, right);
                } else {
                    right_boundary(&node.left, right);
                }
                right.push(node.val);
            }
        }
        fn leaves(node: &Option<Box<TreeNode>>, ans: &mut Vec<i32>) {
            if let Some(node) = node {
                if node.left.is_none() && node.right.is_none() {
                    ans.push(node.val);
                }
                leaves(&node.left, ans);
                leaves(&node.right, ans);
            }
        }
        if root.is_none() { return vec![]; }
        let mut ans = vec![root.as_ref().unwrap().val];
        left_boundary(&root.as_ref().unwrap().left, &mut ans);
        leaves(&root.as_ref().unwrap().left, &mut ans);
        leaves(&root.as_ref().unwrap().right, &mut ans);
        let mut right = vec![];
        right_boundary(&root.as_ref().unwrap().right, &mut right);
        ans.extend(right.into_iter().rev());
        ans
    }
}

Complexity

⏰ Time complexity: O(n) — Each node is visited at most once.
🧺 Space complexity: O(h) — h is the height of the tree (recursion stack).

Problem#

Examples#

Solution#

Method 1 – DFS for Left Boundary, Leaves, and Right Boundary#

Intuition#

Approach#

Code#

Complexity#