Problem

A perfectly straight street is represented by a number line. The street has street lamp(s) on it and is represented by a 2D integer array lights. Each lights[i] = [positioni, rangei] indicates that there is a street lamp at position positioni that lights up the area from [positioni - rangei, positioni + rangei] (inclusive).

The brightness of a position p is defined as the number of street lamp that light up the position p.

Given lights, return thebrightest position on the street. If there are multiple brightest positions, return thesmallest one.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

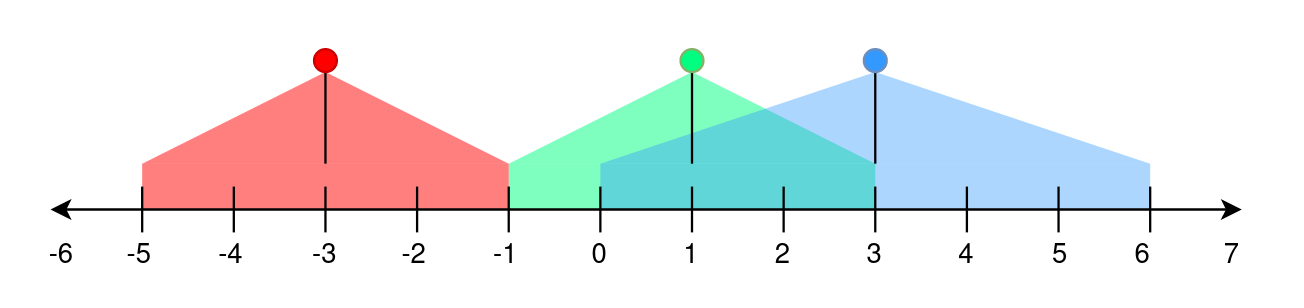
Input: lights = [[-3,2],[1,2],[3,3]]
Output: -1
Explanation:
The first street lamp lights up the area from [(-3) - 2, (-3) + 2] = [-5, -1].
The second street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3].
The third street lamp lights up the area from [3 - 3, 3 + 3] = [0, 6].

Position -1 has a brightness of 2, illuminated by the first and second street light.
Positions 0, 1, 2, and 3 have a brightness of 2, illuminated by the second and third street light.
Out of all these positions, -1 is the smallest, so return it.

Example 2:

1
2
3
4
5
6
7
8

Input: lights = [[1,0],[0,1]]
Output: 1
Explanation:
The first street lamp lights up the area from [1 - 0, 1 + 0] = [1, 1].
The second street lamp lights up the area from [0 - 1, 0 + 1] = [-1, 1].

Position 1 has a brightness of 2, illuminated by the first and second street light.
Return 1 because it is the brightest position on the street.

Example 3:

1
2
3
4
5
6
7

Input: lights = [[1,2]]
Output: -1
Explanation:
The first street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3].

Positions -1, 0, 1, 2, and 3 have a brightness of 1, illuminated by the first street light.
Out of all these positions, -1 is the smallest, so return it.

Constraints:

  • 1 <= lights.length <= 10^5
  • lights[i].length == 2
  • -108 <= positioni <= 10^8
  • 0 <= rangei <= 10^8

Solution

Method 1 – Prefix Sum (Sweep Line)

Intuition

We can use a sweep line (prefix sum) approach: for each lamp, mark +1 at the start of its range and -1 after the end. Then, by sweeping through the sorted positions, we can track the current brightness and find the position with the maximum brightness.

Approach

  1. For each lamp, add +1 at (position - range) and -1 at (position + range + 1) in a map.
  2. Sort all the keys (positions) in the map.
  3. Sweep through the positions, maintaining a running sum (current brightness).
  4. Track the maximum brightness and the smallest position where it occurs.
  5. Return the smallest position with the maximum brightness.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int brightestPosition(vector<vector<int>>& lights) {
        map<long long, int> diff;
        for (auto& l : lights) {
            diff[l[0] - l[1]]++;
            diff[l[0] + l[1] + 1]--;
        }
        int ans = 0, maxb = 0, cur = 0;
        for (auto& [pos, d] : diff) {
            cur += d;
            if (cur > maxb) {
                maxb = cur;
                ans = pos;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

func brightestPosition(lights [][]int) int {
    diff := map[int]int{}
    for _, l := range lights {
        diff[l[0]-l[1]]++
        diff[l[0]+l[1]+1]--
    }
    keys := make([]int, 0, len(diff))
    for k := range diff { keys = append(keys, k) }
    sort.Ints(keys)
    ans, maxb, cur := 0, 0, 0
    for _, pos := range keys {
        cur += diff[pos]
        if cur > maxb {
            maxb = cur
            ans = pos
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
    public int brightestPosition(int[][] lights) {
        TreeMap<Integer, Integer> diff = new TreeMap<>();
        for (int[] l : lights) {
            diff.put(l[0] - l[1], diff.getOrDefault(l[0] - l[1], 0) + 1);
            diff.put(l[0] + l[1] + 1, diff.getOrDefault(l[0] + l[1] + 1, 0) - 1);
        }
        int ans = 0, maxb = 0, cur = 0;
        for (int pos : diff.keySet()) {
            cur += diff.get(pos);
            if (cur > maxb) {
                maxb = cur;
                ans = pos;
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    fun brightestPosition(lights: Array<IntArray>): Int {
        val diff = sortedMapOf<Int, Int>()
        for (l in lights) {
            diff[l[0] - l[1]] = diff.getOrDefault(l[0] - l[1], 0) + 1
            diff[l[0] + l[1] + 1] = diff.getOrDefault(l[0] + l[1] + 1, 0) - 1
        }
        var ans = 0
        var maxb = 0
        var cur = 0
        for ((pos, d) in diff) {
            cur += d
            if (cur > maxb) {
                maxb = cur
                ans = pos
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def brightestPosition(self, lights: list[list[int]]) -> int:
        from collections import defaultdict
        diff: dict[int, int] = defaultdict(int)
        for pos, rng in lights:
            diff[pos - rng] += 1
            diff[pos + rng + 1] -= 1
        ans = maxb = cur = 0
        for pos in sorted(diff):
            cur += diff[pos]
            if cur > maxb:
                maxb = cur
                ans = pos
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

use std::collections::BTreeMap;
impl Solution {
    pub fn brightest_position(lights: Vec<Vec<i32>>) -> i32 {
        let mut diff = BTreeMap::new();
        for l in &lights {
            *diff.entry(l[0] - l[1]).or_insert(0) += 1;
            *diff.entry(l[0] + l[1] + 1).or_insert(0) -= 1;
        }
        let (mut ans, mut maxb, mut cur) = (0, 0, 0);
        for (&pos, &d) in &diff {
            cur += d;
            if cur > maxb {
                maxb = cur;
                ans = pos;
            }
        }
        ans
    }
}

Complexity

  • ⏰ Time complexity: O(n log n) — Sorting the positions.
  • 🧺 Space complexity: O(n) — For the difference map.