Build Binary Expression Tree From Infix Expression
Problem
A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (numbers), and internal nodes (nodes with 2 children) correspond to the operators '+' (addition), '-' (subtraction), '*' (multiplication), and '/' (division).
For each internal node with operator o, the infix expression it represents is (A o B), where A is the expression the left subtree represents and B is the expression the right subtree represents.
You are given a string s, an infix expression containing operands, the operators described above, and parentheses '(' and ')'.
Return _any validbinary expression tree , whose in-order traversal reproduces _s after omitting the parenthesis from it.
Please note that order of operations applies ins. That is, expressions in parentheses are evaluated first, and multiplication and division happen before addition and subtraction.
Operands must also appear in the same order in both s and the in-order traversal of the tree.
Examples
Example 1:
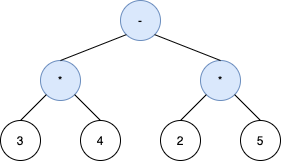
Input: s = "3*4-2*5"
Output: [-,*,*,3,4,2,5]
Explanation: The tree above is the only valid tree whose inorder traversal produces s.
Example 2:
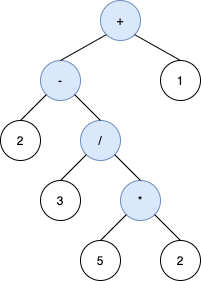
Input: s = "2-3/(5*2)+1"
Output: [+,-,1,2,/,null,null,null,null,3,*,null,null,5,2]
Explanation: The inorder traversal of the tree above is 2-3/5*2+1 which is the same as s without the parenthesis. The tree also produces the correct result and its operands are in the same order as they appear in s.
The tree below is also a valid binary expression tree with the same inorder traversal as s, but it not a valid answer because it does not evaluate to the same value.
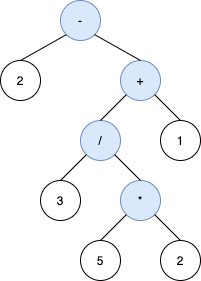
The third tree below is also not valid. Although it produces the same result and is equivalent to the above trees, its inorder traversal does not produce s and its operands are not in the same order as s.
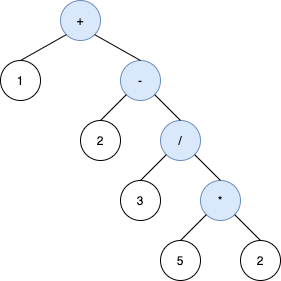
Example 3:
Input: s = "1+2+3+4+5"
Output: [+,+,5,+,4,null,null,+,3,null,null,1,2]
Explanation: The tree [+,+,5,+,+,null,null,1,2,3,4] is also one of many other valid trees.
Constraints:
1 <= s.length <= 100sconsists of digits and the characters'(',')','+','-','*', and'/'.- Operands in
sare exactly 1 digit. - It is guaranteed that
sis a valid expression.
Solution
Method 1: Shunting Yard Algorithm + Tree Construction
Intuition
We use the shunting yard algorithm to convert the infix expression to a binary expression tree. We use two stacks: one for operators and one for tree nodes. When we see an operand, we create a node. When we see an operator, we pop nodes and build subtrees according to precedence and associativity.
Approach
- Use two stacks: one for operators, one for tree nodes.
- For each character in the string:
- If digit: create a node and push to node stack.
- If '(': push to operator stack.
- If ')': pop operators and build subtrees until '('.
- If operator: pop and build subtrees while precedence is higher or equal, then push operator.
- At the end, pop remaining operators and build subtrees.
Code
C++
#include <stack>
#include <string>
using namespace std;
struct Node {
string val;
Node *left, *right;
Node(string v) : val(v), left(nullptr), right(nullptr) {}
Node(string v, Node* l, Node* r) : val(v), left(l), right(r) {}
};
class Solution {
int precedence(char op) {
if (op == '+' || op == '-') return 1;
if (op == '*' || op == '/') return 2;
return 0;
}
void build(stack<char>& ops, stack<Node*>& nodes) {
char op = ops.top(); ops.pop();
Node* r = nodes.top(); nodes.pop();
Node* l = nodes.top(); nodes.pop();
nodes.push(new Node(string(1, op), l, r));
}
public:
Node* buildTree(string s) {
stack<char> ops;
stack<Node*> nodes;
int i = 0, n = s.size();
while (i < n) {
char c = s[i];
if (isdigit(c)) {
nodes.push(new Node(string(1, c)));
i++;
} else if (c == '(') {
ops.push('(');
i++;
} else if (c == ')') {
while (ops.top() != '(') build(ops, nodes);
ops.pop();
i++;
} else {
while (!ops.empty() && ops.top() != '(' && precedence(ops.top()) >= precedence(c))
build(ops, nodes);
ops.push(c);
i++;
}
}
while (!ops.empty()) build(ops, nodes);
return nodes.top();
}
};
Go
type Node struct {
Val string
Left, Right *Node
}
func buildTree(s string) *Node {
precedence := func(op byte) int {
if op == '+' || op == '-' { return 1 }
if op == '*' || op == '/' { return 2 }
return 0
}
var ops []byte
var nodes []*Node
build := func() {
op := ops[len(ops)-1]
ops = ops[:len(ops)-1]
r := nodes[len(nodes)-1]
nodes = nodes[:len(nodes)-1]
l := nodes[len(nodes)-1]
nodes = nodes[:len(nodes)-1]
nodes = append(nodes, &Node{string(op), l, r})
}
for i := 0; i < len(s); {
c := s[i]
if c >= '0' && c <= '9' {
nodes = append(nodes, &Node{string(c), nil, nil})
i++
} else if c == '(' {
ops = append(ops, c)
i++
} else if c == ')' {
for ops[len(ops)-1] != '(' { build() }
ops = ops[:len(ops)-1]
i++
} else {
for len(ops) > 0 && ops[len(ops)-1] != '(' && precedence(ops[len(ops)-1]) >= precedence(c) {
build()
}
ops = append(ops, c)
i++
}
}
for len(ops) > 0 { build() }
return nodes[len(nodes)-1]
}
Java
class Node {
String val;
Node left, right;
Node(String v) { val = v; }
Node(String v, Node l, Node r) { val = v; left = l; right = r; }
}
class Solution {
int precedence(char op) {
if (op == '+' || op == '-') return 1;
if (op == '*' || op == '/') return 2;
return 0;
}
public Node buildTree(String s) {
Stack<Character> ops = new Stack<>();
Stack<Node> nodes = new Stack<>();
int i = 0, n = s.length();
while (i < n) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
nodes.push(new Node(String.valueOf(c)));
i++;
} else if (c == '(') {
ops.push('(');
i++;
} else if (c == ')') {
while (ops.peek() != '(') build(ops, nodes);
ops.pop();
i++;
} else {
while (!ops.isEmpty() && ops.peek() != '(' && precedence(ops.peek()) >= precedence(c))
build(ops, nodes);
ops.push(c);
i++;
}
}
while (!ops.isEmpty()) build(ops, nodes);
return nodes.peek();
}
void build(Stack<Character> ops, Stack<Node> nodes) {
char op = ops.pop();
Node r = nodes.pop(), l = nodes.pop();
nodes.push(new Node(String.valueOf(op), l, r));
}
}
Kotlin
data class Node(val v: String, var left: Node? = null, var right: Node? = null)
class Solution {
fun buildTree(s: String): Node? {
fun precedence(op: Char) = when (op) { '+', '-' -> 1; '*', '/' -> 2; else -> 0 }
val ops = ArrayDeque<Char>()
val nodes = ArrayDeque<Node>()
fun build() {
val op = ops.removeLast()
val r = nodes.removeLast()
val l = nodes.removeLast()
nodes.addLast(Node(op.toString(), l, r))
}
var i = 0
while (i < s.length) {
val c = s[i]
when {
c.isDigit() -> { nodes.addLast(Node(c.toString())); i++ }
c == '(' -> { ops.addLast('('); i++ }
c == ')' -> { while (ops.last() != '(') build(); ops.removeLast(); i++ }
else -> {
while (ops.isNotEmpty() && ops.last() != '(' && precedence(ops.last()) >= precedence(c)) build()
ops.addLast(c); i++
}
}
}
while (ops.isNotEmpty()) build()
return nodes.last()
}
}
Python
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def buildTree(self, s: str) -> 'Node':
def precedence(op):
if op in ('+', '-'): return 1
if op in ('*', '/'): return 2
return 0
ops, nodes = [], []
i = 0
while i < len(s):
if s[i].isdigit():
nodes.append(Node(s[i]))
i += 1
elif s[i] == '(':
ops.append('(')
i += 1
elif s[i] == ')':
while ops and ops[-1] != '(': build()
ops.pop()
i += 1
else:
while ops and ops[-1] != '(' and precedence(ops[-1]) >= precedence(s[i]):
build()
ops.append(s[i])
i += 1
while ops: build()
return nodes[-1]
def build():
op = ops.pop()
r = nodes.pop()
l = nodes.pop()
nodes.append(Node(op, l, r))
Rust
pub struct Node {
pub val: String,
pub left: Option<Box<Node>>,
pub right: Option<Box<Node>>,
}
impl Node {
pub fn new(val: String) -> Self {
Node { val, left: None, right: None }
}
pub fn with_children(val: String, left: Node, right: Node) -> Self {
Node { val, left: Some(Box::new(left)), right: Some(Box::new(right)) }
}
}
pub fn build_tree(s: &str) -> Node {
fn precedence(op: char) -> i32 {
match op {
'+' | '-' => 1,
'*' | '/' => 2,
_ => 0,
}
}
let mut ops = Vec::new();
let mut nodes = Vec::new();
let mut i = 0;
let cs: Vec<char> = s.chars().collect();
let mut build = |ops: &mut Vec<char>, nodes: &mut Vec<Node>| {
let op = ops.pop().unwrap();
let r = nodes.pop().unwrap();
let l = nodes.pop().unwrap();
nodes.push(Node::with_children(op.to_string(), l, r));
};
while i < cs.len() {
let c = cs[i];
if c.is_ascii_digit() {
nodes.push(Node::new(c.to_string()));
i += 1;
} else if c == '(' {
ops.push(c);
i += 1;
} else if c == ')' {
while *ops.last().unwrap() != '(' { build(&mut ops, &mut nodes); }
ops.pop();
i += 1;
} else {
while !ops.is_empty() && *ops.last().unwrap() != '(' && precedence(*ops.last().unwrap()) >= precedence(c) {
build(&mut ops, &mut nodes);
}
ops.push(c);
i += 1;
}
}
while !ops.is_empty() { build(&mut ops, &mut nodes); }
nodes.pop().unwrap()
}
Complexity
- ⏰ Time complexity:
O(n) - 🧺 Space complexity:
O(n)