Building Boxes

Problem

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

• You can place the boxes anywhere on the floor.
• If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return theminimum possible number of boxes touching the floor.

Examples

Example 1

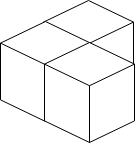
Input: n = 3
Output: 3
Explanation: The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 2

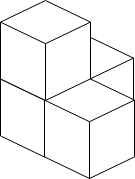
Input: n = 4
Output: 3
Explanation: The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 3

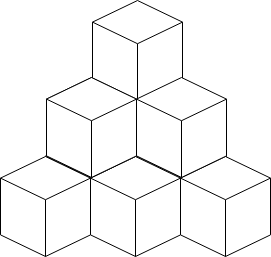
Input: n = 10
Output: 6
Explanation: The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.

Constraints

• 1 <= n <= 10^9

Solution

Method 1: Greedy + Binary Search (Optimal)

Intuition

The problem is equivalent to stacking boxes in a corner to form a 3D pyramid. The minimum number of boxes touching the floor is the minimum base size such that the total number of boxes in the pyramid is at least n.

Approach

• The total number of boxes in a pyramid of height h is h*(h+1)*(h+2)/6 (sum of tetrahedral numbers).
• For a given base size k, the maximum number of boxes that can be stacked is k*(k+1)/2 (triangular number).
• Use binary search to find the minimum base size such that the total number of boxes is at least n.

Code

Python

class Solution:
    def minimumBoxes(self, n: int) -> int:
        # Find the largest h such that h*(h+1)*(h+2)//6 <= n
        h = 0
        while (h+1)*(h+2)*(h+3)//6 <= n:
            h += 1
        used = h*(h+1)*(h+2)//6
        # Now, fill the remaining boxes on the floor
        res = h*(h+1)//2
        left = n - used
        if left == 0:
            return res
        # Add boxes one by one to the next row
        k = 1
        while left > 0:
            res += 1
            left -= k
            k += 1
        return res

Java

class Solution {
    public int minimumBoxes(int n) {
        int h = 0;
        while ((long)(h+1)*(h+2)*(h+3)/6 <= n) h++;
        int used = h*(h+1)*(h+2)/6;
        int res = h*(h+1)/2;
        int left = n - used;
        if (left == 0) return res;
        int k = 1;
        while (left > 0) {
            res++;
            left -= k++;
        }
        return res;
    }
}

C++

class Solution {
public:
    int minimumBoxes(int n) {
        int h = 0;
        while ((long long)(h+1)*(h+2)*(h+3)/6 <= n) h++;
        int used = h*(h+1)*(h+2)/6;
        int res = h*(h+1)/2;
        int left = n - used;
        if (left == 0) return res;
        int k = 1;
        while (left > 0) {
            res++;
            left -= k++;
        }
        return res;
    }
};

Go

func minimumBoxes(n int) int {
    h := 0
    for (h+1)*(h+2)*(h+3)/6 <= n {
        h++
    }
    used := h*(h+1)*(h+2)/6
    res := h*(h+1)/2
    left := n - used
    if left == 0 {
        return res
    }
    k := 1
    for left > 0 {
        res++
        left -= k
        k++
    }
    return res
}

Kotlin

class Solution {
    fun minimumBoxes(n: Int): Int {
        var h = 0
        while ((h+1).toLong()*(h+2)*(h+3)/6 <= n) h++
        val used = h*(h+1)*(h+2)/6
        var res = h*(h+1)/2
        var left = n - used
        if (left == 0) return res
        var k = 1
        while (left > 0) {
            res++
            left -= k
            k++
        }
        return res
    }
}

Rust

impl Solution {
    pub fn minimum_boxes(n: i32) -> i32 {
        let mut h = 0;
        while (h+1)*(h+2)*(h+3)/6 <= n {
            h += 1;
        }
        let used = h*(h+1)*(h+2)/6;
        let mut res = h*(h+1)/2;
        let mut left = n - used;
        if left == 0 {
            return res;
        }
        let mut k = 1;
        while left > 0 {
            res += 1;
            left -= k;
            k += 1;
        }
        res
    }
}

Complexity

• ⏰ Time complexity: O(∛n)
• 🧺 Space complexity: O(1)