Problem

On a campus represented on the X-Y plane, there are n workers and m bikes, with n <= m.

You are given an array workers of length n where workers[i] = [xi, yi] is the position of the ith worker. You are also given an array bikes of length m where bikes[j] = [xj, yj] is the position of the jth bike. All the given positions are unique.

Assign a bike to each worker. Among the available bikes and workers, we choose the (workeri, bikej) pair with the shortest Manhattan distance between each other and assign the bike to that worker.

If there are multiple (workeri, bikej) pairs with the same shortest Manhattan distance , we choose the pair with the smallest worker index. If there are multiple ways to do that, we choose the pair with the smallest bike index. Repeat this process until there are no available workers.

Return an arrayanswer of lengthn , whereanswer[i]_is the index (0-indexed) of the bike that the _ith worker is assigned to.

The Manhattan distance between two points p1 and p2 is Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|.

Examples

Example 1:

1
2
3

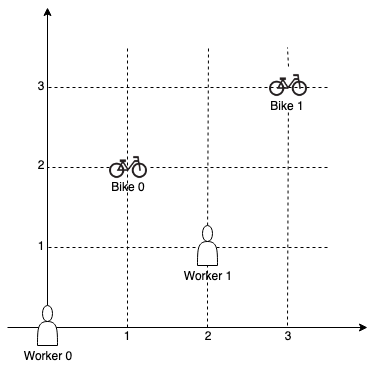
Input: workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
Output: [1,0]
Explanation: Worker 1 grabs Bike 0 as they are closest (without ties), and Worker 0 is assigned Bike 1. So the output is [1, 0].

Example 2: 

1
2
3

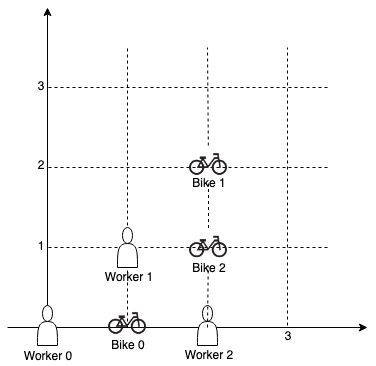
Input: workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
Output: [0,2,1]
Explanation: Worker 0 grabs Bike 0 at first. Worker 1 and Worker 2 share the same distance to Bike 2, thus Worker 1 is assigned to Bike 2, and Worker 2 will take Bike 1. So the output is [0,2,1].

Constraints:

  • n == workers.length
  • m == bikes.length
  • 1 <= n <= m <= 1000
  • workers[i].length == bikes[j].length == 2
  • 0 <= xi, yi < 1000
  • 0 <= xj, yj < 1000
  • All worker and bike locations are unique.

Solution

Method 1 – Greedy Assignment with Sorting

Intuition

We want to assign each worker the closest available bike, breaking ties by worker index and then bike index. By precomputing all possible (worker, bike) pairs with their Manhattan distances and sorting them, we can greedily assign bikes to workers in the required order.

Approach

  1. For every worker and every bike, compute the Manhattan distance and store (distance, worker index, bike index) in a list.
  2. Sort the list by distance, then by worker index, then by bike index.
  3. Initialize arrays to track assigned workers and bikes.
  4. Iterate through the sorted list:
    • If the worker and bike are both unassigned, assign the bike to the worker.
    • Continue until all workers are assigned.
  5. Return the assignment array.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        int n = workers.size(), m = bikes.size();
        vector<tuple<int, int, int>> pairs;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                int dist = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
                pairs.emplace_back(dist, i, j);
            }
        }
        sort(pairs.begin(), pairs.end());
        vector<int> ans(n, -1);
        vector<bool> usedB(m, false);
        int assigned = 0;
        for (auto& [d, i, j] : pairs) {
            if (ans[i] == -1 && !usedB[j]) {
                ans[i] = j;
                usedB[j] = true;
                assigned++;
                if (assigned == n) break;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

func assignBikes(workers [][]int, bikes [][]int) []int {
    n, m := len(workers), len(bikes)
    type pair struct{ d, i, j int }
    var pairs []pair
    for i := 0; i < n; i++ {
        for j := 0; j < m; j++ {
            d := abs(workers[i][0]-bikes[j][0]) + abs(workers[i][1]-bikes[j][1])
            pairs = append(pairs, pair{d, i, j})
        }
    }
    sort.Slice(pairs, func(a, b int) bool {
        if pairs[a].d != pairs[b].d {
            return pairs[a].d < pairs[b].d
        }
        if pairs[a].i != pairs[b].i {
            return pairs[a].i < pairs[b].i
        }
        return pairs[a].j < pairs[b].j
    })
    ans := make([]int, n)
    for i := range ans {
        ans[i] = -1
    }
    usedB := make([]bool, m)
    assigned := 0
    for _, p := range pairs {
        if ans[p.i] == -1 && !usedB[p.j] {
            ans[p.i] = p.j
            usedB[p.j] = true
            assigned++
            if assigned == n {
                break
            }
        }
    }
    return ans
}
func abs(x int) int { if x < 0 { return -x }; return x }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    public int[] assignBikes(int[][] workers, int[][] bikes) {
        int n = workers.length, m = bikes.length;
        List<int[]> pairs = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int d = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1]);
                pairs.add(new int[]{d, i, j});
            }
        }
        pairs.sort((a, b) -> a[0] != b[0] ? a[0] - b[0] : (a[1] != b[1] ? a[1] - b[1] : a[2] - b[2]));
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        boolean[] usedB = new boolean[m];
        int assigned = 0;
        for (int[] p : pairs) {
            int d = p[0], i = p[1], j = p[2];
            if (ans[i] == -1 && !usedB[j]) {
                ans[i] = j;
                usedB[j] = true;
                assigned++;
                if (assigned == n) break;
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    fun assignBikes(workers: Array<IntArray>, bikes: Array<IntArray>): IntArray {
        val n = workers.size
        val m = bikes.size
        val pairs = mutableListOf<Triple<Int, Int, Int>>()
        for (i in 0 until n) {
            for (j in 0 until m) {
                val d = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1])
                pairs.add(Triple(d, i, j))
            }
        }
        pairs.sortWith(compareBy({ it.first }, { it.second }, { it.third }))
        val ans = IntArray(n) { -1 }
        val usedB = BooleanArray(m)
        var assigned = 0
        for ((d, i, j) in pairs) {
            if (ans[i] == -1 && !usedB[j]) {
                ans[i] = j
                usedB[j] = true
                assigned++
                if (assigned == n) break
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution:
    def assignBikes(self, workers: list[list[int]], bikes: list[list[int]]) -> list[int]:
        n, m = len(workers), len(bikes)
        pairs = []
        for i in range(n):
            for j in range(m):
                d = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1])
                pairs.append((d, i, j))
        pairs.sort()
        ans = [-1] * n
        usedB = [False] * m
        assigned = 0
        for d, i, j in pairs:
            if ans[i] == -1 and not usedB[j]:
                ans[i] = j
                usedB[j] = True
                assigned += 1
                if assigned == n:
                    break
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

impl Solution {
    pub fn assign_bikes(workers: Vec<Vec<i32>>, bikes: Vec<Vec<i32>>) -> Vec<i32> {
        let n = workers.len();
        let m = bikes.len();
        let mut pairs = vec![];
        for i in 0..n {
            for j in 0..m {
                let d = (workers[i][0] - bikes[j][0]).abs() + (workers[i][1] - bikes[j][1]).abs();
                pairs.push((d, i, j));
            }
        }
        pairs.sort();
        let mut ans = vec![-1; n];
        let mut used_b = vec![false; m];
        let mut assigned = 0;
        for &(d, i, j) in &pairs {
            if ans[i] == -1 && !used_b[j] {
                ans[i] = j as i32;
                used_b[j] = true;
                assigned += 1;
                if assigned == n { break; }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    assignBikes(workers: number[][], bikes: number[][]): number[] {
        const n = workers.length, m = bikes.length;
        const pairs: [number, number, number][] = [];
        for (let i = 0; i < n; i++) {
            for (let j = 0; j < m; j++) {
                const d = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1]);
                pairs.push([d, i, j]);
            }
        }
        pairs.sort((a, b) => a[0] - b[0] || a[1] - b[1] || a[2] - b[2]);
        const ans = Array(n).fill(-1);
        const usedB = Array(m).fill(false);
        let assigned = 0;
        for (const [d, i, j] of pairs) {
            if (ans[i] === -1 && !usedB[j]) {
                ans[i] = j;
                usedB[j] = true;
                assigned++;
                if (assigned === n) break;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n*m*log(n*m))
  • 🧺 Space complexity: O(n*m)