Campus Bikes II

Problem

On a campus represented as a 2D grid, there are n workers and m bikes, with n <= m. Each worker and bike is a 2D coordinate on this grid.

We assign one unique bike to each worker so that the sum of the Manhattan distances between each worker and their assigned bike is minimized.

Return the minimum possible sum of Manhattan distances between each worker and their assigned bike.

The Manhattan distance between two points p1 and p2 is Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|.

Examples

Example 1:

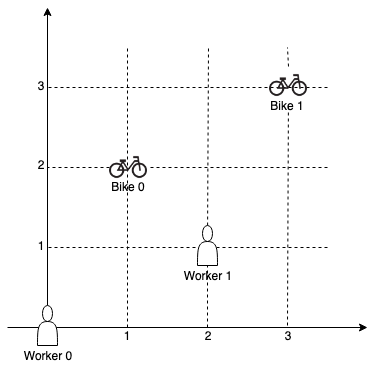
Input: workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
Output: 6
Explanation: 
We assign bike 0 to worker 0, bike 1 to worker 1. The Manhattan distance of both assignments is 3, so the output is 6.

Example 2:

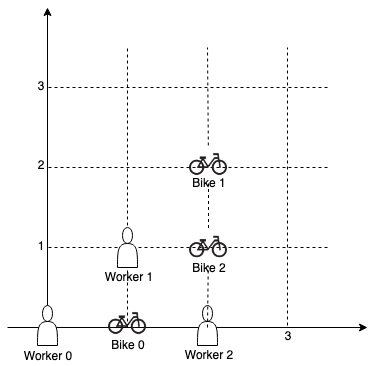
Input: workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
Output: 4
Explanation:
We first assign bike 0 to worker 0, then assign bike 1 to worker 1 or worker 2, bike 2 to worker 2 or worker 1. Both assignments lead to sum of the Manhattan distances as 4.

Example 3:

    Input: workers = [[0,0],[1,0],[2,0],[3,0],[4,0]], bikes = [[0,999],[1,999],[2,999],[3,999],[4,999]]
    Output: 4995

Constraints:

• n == workers.length
• m == bikes.length
• 1 <= n <= m <= 10
• workers[i].length == 2
• bikes[i].length == 2
• 0 <= workers[i][0], workers[i][1], bikes[i][0], bikes[i][1] < 1000
• All the workers and the bikes locations are unique.

Solution

Method 1 – Bitmask DP (Backtracking with Memoization)

Intuition

We want to assign each worker a unique bike such that the total Manhattan distance is minimized. Since n ≤ m and n ≤ 10, we can use bitmask dynamic programming to efficiently try all assignments and cache results.

Approach

1. Use a recursive function with parameters: current worker index and a bitmask of used bikes.
2. For each available bike, try assigning it to the current worker:
   • Mark the bike as used in the bitmask.
   • Recurse to the next worker.
   • Add the Manhattan distance for this assignment.
3. Use memoization to cache results for (worker, used mask).
4. Base case: if all workers are assigned, return 0.
5. Return the minimum total distance found.

Code

C++

class Solution {
public:
    int assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        int n = workers.size(), m = bikes.size();
        vector<vector<int>> memo(n, vector<int>(1 << m, -1));
        function<int(int, int)> dp = [&](int i, int mask) {
            if (i == n) return 0;
            if (memo[i][mask] != -1) return memo[i][mask];
            int ans = INT_MAX;
            for (int j = 0; j < m; ++j) {
                if (!(mask & (1 << j))) {
                    int d = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
                    ans = min(ans, d + dp(i + 1, mask | (1 << j)));
                }
            }
            return memo[i][mask] = ans;
        };
        return dp(0, 0);
    }
};

Go

func assignBikes(workers [][]int, bikes [][]int) int {
    n, m := len(workers), len(bikes)
    memo := make([][]int, n)
    for i := range memo {
        memo[i] = make([]int, 1<<m)
        for j := range memo[i] {
            memo[i][j] = -1
        }
    }
    var dp func(int, int) int
    dp = func(i, mask int) int {
        if i == n {
            return 0
        }
        if memo[i][mask] != -1 {
            return memo[i][mask]
        }
        ans := 1 << 30
        for j := 0; j < m; j++ {
            if mask&(1<<j) == 0 {
                d := abs(workers[i][0]-bikes[j][0]) + abs(workers[i][1]-bikes[j][1])
                ans = min(ans, d+dp(i+1, mask|(1<<j)))
            }
        }
        memo[i][mask] = ans
        return ans
    }
    return dp(0, 0)
}
func abs(x int) int { if x < 0 { return -x }; return x }
func min(a, b int) int { if a < b { return a }; return b }

Java

class Solution {
    public int assignBikes(int[][] workers, int[][] bikes) {
        int n = workers.length, m = bikes.length;
        int[][] memo = new int[n][1 << m];
        for (int[] row : memo) Arrays.fill(row, -1);
        return dp(0, 0, workers, bikes, memo);
    }
    private int dp(int i, int mask, int[][] workers, int[][] bikes, int[][] memo) {
        if (i == workers.length) return 0;
        if (memo[i][mask] != -1) return memo[i][mask];
        int ans = Integer.MAX_VALUE;
        for (int j = 0; j < bikes.length; j++) {
            if ((mask & (1 << j)) == 0) {
                int d = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1]);
                ans = Math.min(ans, d + dp(i + 1, mask | (1 << j), workers, bikes, memo));
            }
        }
        return memo[i][mask] = ans;
    }
}

Kotlin

class Solution {
    fun assignBikes(workers: Array<IntArray>, bikes: Array<IntArray>): Int {
        val n = workers.size
        val m = bikes.size
        val memo = Array(n) { IntArray(1 shl m) { -1 } }
        fun dp(i: Int, mask: Int): Int {
            if (i == n) return 0
            if (memo[i][mask] != -1) return memo[i][mask]
            var ans = Int.MAX_VALUE
            for (j in 0 until m) {
                if ((mask and (1 shl j)) == 0) {
                    val d = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1])
                    ans = minOf(ans, d + dp(i + 1, mask or (1 shl j)))
                }
            }
            memo[i][mask] = ans
            return ans
        }
        return dp(0, 0)
    }
}

Python

class Solution:
    def assignBikes(self, workers: list[list[int]], bikes: list[list[int]]) -> int:
        from functools import lru_cache
        n, m = len(workers), len(bikes)
        @lru_cache(None)
        def dp(i: int, mask: int) -> int:
            if i == n:
                return 0
            ans = float('inf')
            for j in range(m):
                if not (mask & (1 << j)):
                    d = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1])
                    ans = min(ans, d + dp(i + 1, mask | (1 << j)))
            return ans
        return dp(0, 0)

Rust

use std::collections::HashMap;
impl Solution {
    pub fn assign_bikes(workers: Vec<Vec<i32>>, bikes: Vec<Vec<i32>>) -> i32 {
        fn dp(i: usize, mask: usize, n: usize, m: usize, workers: &Vec<Vec<i32>>, bikes: &Vec<Vec<i32>>, memo: &mut HashMap<(usize, usize), i32>) -> i32 {
            if i == n { return 0; }
            if let Some(&v) = memo.get(&(i, mask)) { return v; }
            let mut ans = i32::MAX;
            for j in 0..m {
                if mask & (1 << j) == 0 {
                    let d = (workers[i][0] - bikes[j][0]).abs() + (workers[i][1] - bikes[j][1]).abs();
                    ans = ans.min(d + dp(i + 1, mask | (1 << j), n, m, workers, bikes, memo));
                }
            }
            memo.insert((i, mask), ans);
            ans
        }
        let n = workers.len();
        let m = bikes.len();
        let mut memo = HashMap::new();
        dp(0, 0, n, m, &workers, &bikes, &mut memo)
    }
}

TypeScript

class Solution {
    assignBikes(workers: number[][], bikes: number[][]): number {
        const n = workers.length, m = bikes.length;
        const memo = Array.from({ length: n }, () => Array(1 << m).fill(-1));
        function dp(i: number, mask: number): number {
            if (i === n) return 0;
            if (memo[i][mask] !== -1) return memo[i][mask];
            let ans = Infinity;
            for (let j = 0; j < m; j++) {
                if ((mask & (1 << j)) === 0) {
                    const d = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1]);
                    ans = Math.min(ans, d + dp(i + 1, mask | (1 << j)));
                }
            }
            memo[i][mask] = ans;
            return ans;
        }
        return dp(0, 0);
    }
}

Complexity

• ⏰ Time complexity: O(n * 2^m * m)
• 🧺 Space complexity: O(n * 2^m)