Problem

A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.

The graph is given as follows: graph[a] is a list of all nodes b such that ab is an edge of the graph.

The mouse starts at node 1 and goes first, the cat starts at node 2 and goes second, and there is a hole at node 0.

During each player’s turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it must travel to any node in graph[1].

Additionally, it is not allowed for the Cat to travel to the Hole (node 0).

Then, the game can end in three ways:

  • If ever the Cat occupies the same node as the Mouse, the Cat wins.
  • If ever the Mouse reaches the Hole, the Mouse wins.
  • If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player’s turn to move), the game is a draw.

Given a graph, and assuming both players play optimally, return

  • 1 if the mouse wins the game,
  • 2 if the cat wins the game, or
  • 0 if the game is a draw.

Examples

Example 1

1
2

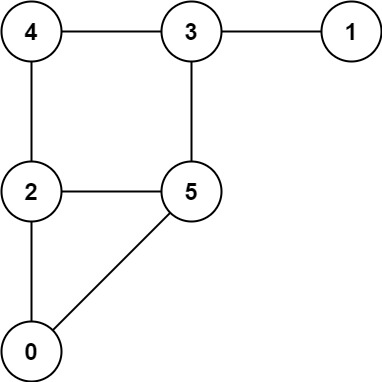
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
Output: 0

Example 2

1
2

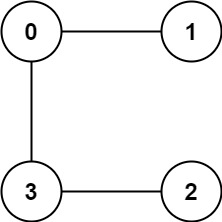
Input: graph = [[1,3],[0],[3],[0,2]]
Output: 1

Constraints

  • 3 <= graph.length <= 50
  • 1 <= graph[i].length < graph.length
  • 0 <= graph[i][j] < graph.length
  • graph[i][j] != i
  • graph[i] is unique.
  • The mouse and the cat can always move.

Solution

Method 1 – DP with Memoization (Game Theory)

Intuition

We model the game as a state (mouse position, cat position, turn) and use DP with memoization to avoid recomputation. The mouse tries to reach the hole, the cat tries to catch the mouse, and a draw occurs if a state repeats. We recursively simulate all possible moves for both players, marking win/loss/draw for each state.

Approach

  1. Define a DP function: dp(mouse, cat, turn) where turn is the number of moves taken so far.
  2. Base cases:
    • If turn >= 2*n (where n is the number of nodes), return 0 (draw).
    • If mouse == 0, return 1 (mouse wins).
    • If mouse == cat, return 2 (cat wins).
  3. If it’s the mouse’s turn (even turn):
    • For each neighbor of mouse, recursively call dp(next_mouse, cat, turn+1).
    • If any move leads to mouse win, return 1.
    • If all moves lead to cat win, return 2.
    • Otherwise, return 0 (draw).
  4. If it’s the cat’s turn (odd turn):
    • For each neighbor of cat (except 0), recursively call dp(mouse, next_cat, turn+1).
    • If any move leads to cat win, return 2.
    • If all moves lead to mouse win, return 1.
    • Otherwise, return 0 (draw).
  5. Use memoization to cache results for (mouse, cat, turn).
  6. Start with dp(1, 2, 0).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
public:
    int catMouseGame(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<vector<vector<int>>> memo(n, vector<vector<int>>(n, vector<int>(2*n, -1)));
        function<int(int,int,int)> dp = [&](int mouse, int cat, int t) {
            if (t >= 2*n) return 0;
            if (mouse == 0) return 1;
            if (mouse == cat) return 2;
            if (memo[mouse][cat][t] != -1) return memo[mouse][cat][t];
            int turn = t%2;
            if (turn == 0) {
                bool draw = false;
                for (int next : graph[mouse]) {
                    int res = dp(next, cat, t+1);
                    if (res == 1) return memo[mouse][cat][t] = 1;
                    if (res == 0) draw = true;
                }
                return memo[mouse][cat][t] = draw ? 0 : 2;
            } else {
                bool draw = false;
                for (int next : graph[cat]) {
                    if (next == 0) continue;
                    int res = dp(mouse, next, t+1);
                    if (res == 2) return memo[mouse][cat][t] = 2;
                    if (res == 0) draw = true;
                }
                return memo[mouse][cat][t] = draw ? 0 : 1;
            }
        };
        return dp(1,2,0);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

func catMouseGame(graph [][]int) int {
    n := len(graph)
    memo := make([][][]int, n)
    for i := range memo {
        memo[i] = make([][]int, n)
        for j := range memo[i] {
            memo[i][j] = make([]int, 2*n)
            for k := range memo[i][j] {
                memo[i][j][k] = -1
            }
        }
    }
    var dp func(mouse, cat, t int) int
    dp = func(mouse, cat, t int) int {
        if t >= 2*n {
            return 0
        }
        if mouse == 0 {
            return 1
        }
        if mouse == cat {
            return 2
        }
        if memo[mouse][cat][t] != -1 {
            return memo[mouse][cat][t]
        }
        turn := t % 2
        if turn == 0 {
            draw := false
            for _, next := range graph[mouse] {
                res := dp(next, cat, t+1)
                if res == 1 {
                    memo[mouse][cat][t] = 1
                    return 1
                }
                if res == 0 {
                    draw = true
                }
            }
            if draw {
                memo[mouse][cat][t] = 0
                return 0
            }
            memo[mouse][cat][t] = 2
            return 2
        } else {
            draw := false
            for _, next := range graph[cat] {
                if next == 0 {
                    continue
                }
                res := dp(mouse, next, t+1)
                if res == 2 {
                    memo[mouse][cat][t] = 2
                    return 2
                }
                if res == 0 {
                    draw = true
                }
            }
            if draw {
                memo[mouse][cat][t] = 0
                return 0
            }
            memo[mouse][cat][t] = 1
            return 1
        }
    }
    return dp(1, 2, 0)
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution {
    public int catMouseGame(int[][] graph) {
        int n = graph.length;
        int[][][] memo = new int[n][n][2*n];
        for (int[][] arr2 : memo)
            for (int[] arr : arr2)
                Arrays.fill(arr, -1);
        return dp(1, 2, 0, graph, memo);
    }
    private int dp(int mouse, int cat, int t, int[][] graph, int[][][] memo) {
        int n = graph.length;
        if (t >= 2*n) return 0;
        if (mouse == 0) return 1;
        if (mouse == cat) return 2;
        if (memo[mouse][cat][t] != -1) return memo[mouse][cat][t];
        int turn = t % 2;
        if (turn == 0) {
            boolean draw = false;
            for (int next : graph[mouse]) {
                int res = dp(next, cat, t+1, graph, memo);
                if (res == 1) return memo[mouse][cat][t] = 1;
                if (res == 0) draw = true;
            }
            return memo[mouse][cat][t] = draw ? 0 : 2;
        } else {
            boolean draw = false;
            for (int next : graph[cat]) {
                if (next == 0) continue;
                int res = dp(mouse, next, t+1, graph, memo);
                if (res == 2) return memo[mouse][cat][t] = 2;
                if (res == 0) draw = true;
            }
            return memo[mouse][cat][t] = draw ? 0 : 1;
        }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    fun catMouseGame(graph: Array<IntArray>): Int {
        val n = graph.size
        val memo = Array(n) { Array(n) { IntArray(2 * n) { -1 } } }
        fun dp(mouse: Int, cat: Int, t: Int): Int {
            if (t >= 2 * n) return 0
            if (mouse == 0) return 1
            if (mouse == cat) return 2
            if (memo[mouse][cat][t] != -1) return memo[mouse][cat][t]
            val turn = t % 2
            if (turn == 0) {
                var draw = false
                for (next in graph[mouse]) {
                    val res = dp(next, cat, t + 1)
                    if (res == 1) return memo[mouse][cat][t] = 1
                    if (res == 0) draw = true
                }
                return if (draw) memo[mouse][cat][t] = 0 else memo[mouse][cat][t] = 2
            } else {
                var draw = false
                for (next in graph[cat]) {
                    if (next == 0) continue
                    val res = dp(mouse, next, t + 1)
                    if (res == 2) return memo[mouse][cat][t] = 2
                    if (res == 0) draw = true
                }
                return if (draw) memo[mouse][cat][t] = 0 else memo[mouse][cat][t] = 1
            }
        }
        return dp(1, 2, 0)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution:
    def catMouseGame(self, graph: list[list[int]]) -> int:
        n = len(graph)
        from functools import lru_cache
        @lru_cache(None)
        def dp(mouse: int, cat: int, t: int) -> int:
            if t >= 2 * n:
                return 0
            if mouse == 0:
                return 1
            if mouse == cat:
                return 2
            turn = t % 2
            if turn == 0:
                draw = False
                for nxt in graph[mouse]:
                    res = dp(nxt, cat, t + 1)
                    if res == 1:
                        return 1
                    if res == 0:
                        draw = True
                return 0 if draw else 2
            else:
                draw = False
                for nxt in graph[cat]:
                    if nxt == 0:
                        continue
                    res = dp(mouse, nxt, t + 1)
                    if res == 2:
                        return 2
                    if res == 0:
                        draw = True
                return 0 if draw else 1
        return dp(1, 2, 0)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

use std::collections::HashMap;
impl Solution {
    pub fn cat_mouse_game(graph: Vec<Vec<i32>>) -> i32 {
        let n = graph.len();
        fn dp(mouse: usize, cat: usize, t: usize, n: usize, graph: &Vec<Vec<i32>>, memo: &mut HashMap<(usize, usize, usize), i32>) -> i32 {
            if t >= 2 * n { return 0; }
            if mouse == 0 { return 1; }
            if mouse == cat { return 2; }
            if let Some(&v) = memo.get(&(mouse, cat, t)) { return v; }
            let turn = t % 2;
            let mut res = 0;
            if turn == 0 {
                let mut draw = false;
                for &next in &graph[mouse] {
                    let r = dp(next as usize, cat, t + 1, n, graph, memo);
                    if r == 1 { memo.insert((mouse, cat, t), 1); return 1; }
                    if r == 0 { draw = true; }
                }
                res = if draw { 0 } else { 2 };
            } else {
                let mut draw = false;
                for &next in &graph[cat] {
                    if next == 0 { continue; }
                    let r = dp(mouse, next as usize, t + 1, n, graph, memo);
                    if r == 2 { memo.insert((mouse, cat, t), 2); return 2; }
                    if r == 0 { draw = true; }
                }
                res = if draw { 0 } else { 1 };
            }
            memo.insert((mouse, cat, t), res);
            res
        }
        let mut memo = HashMap::new();
        dp(1, 2, 0, n, &graph, &mut memo)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    catMouseGame(graph: number[][]): number {
        const n = graph.length;
        const memo = Array.from({ length: n }, () => Array.from({ length: n }, () => Array(2 * n).fill(-1)));
        function dp(mouse: number, cat: number, t: number): number {
            if (t >= 2 * n) return 0;
            if (mouse === 0) return 1;
            if (mouse === cat) return 2;
            if (memo[mouse][cat][t] !== -1) return memo[mouse][cat][t];
            const turn = t % 2;
            if (turn === 0) {
                let draw = false;
                for (const next of graph[mouse]) {
                    const res = dp(next, cat, t + 1);
                    if (res === 1) return memo[mouse][cat][t] = 1;
                    if (res === 0) draw = true;
                }
                return memo[mouse][cat][t] = draw ? 0 : 2;
            } else {
                let draw = false;
                for (const next of graph[cat]) {
                    if (next === 0) continue;
                    const res = dp(mouse, next, t + 1);
                    if (res === 2) return memo[mouse][cat][t] = 2;
                    if (res === 0) draw = true;
                }
                return memo[mouse][cat][t] = draw ? 0 : 1;
            }
        }
        return dp(1, 2, 0);
    }
}

Complexity

  • ⏰ Time complexity: O(n^3)
  • 🧺 Space complexity: O(n^3)