Problem

A game is played by a cat and a mouse named Cat and Mouse.

The environment is represented by a grid of size rows x cols, where each element is a wall, floor, player (Cat, Mouse), or food.

  • Players are represented by the characters 'C'(Cat),'M'(Mouse).
  • Floors are represented by the character '.' and can be walked on.
  • Walls are represented by the character '#' and cannot be walked on.
  • Food is represented by the character 'F' and can be walked on.
  • There is only one of each character 'C', 'M', and 'F' in grid.

Mouse and Cat play according to the following rules:

  • Mouse moves first , then they take turns to move.
  • During each turn, Cat and Mouse can jump in one of the four directions (left, right, up, down). They cannot jump over the wall nor outside of the grid.
  • catJump, mouseJump are the maximum lengths Cat and Mouse can jump at a time, respectively. Cat and Mouse can jump less than the maximum length.
  • Staying in the same position is allowed.
  • Mouse can jump over Cat.

The game can end in 4 ways:

  • If Cat occupies the same position as Mouse, Cat wins.
  • If Cat reaches the food first, Cat wins.
  • If Mouse reaches the food first, Mouse wins.
  • If Mouse cannot get to the food within 1000 turns, Cat wins.

Given a rows x cols matrix grid and two integers catJump and mouseJump, return true if Mouse can win the game if both Cat and Mouse play optimally, otherwise returnfalse.

Examples

Example 1

1
2
3

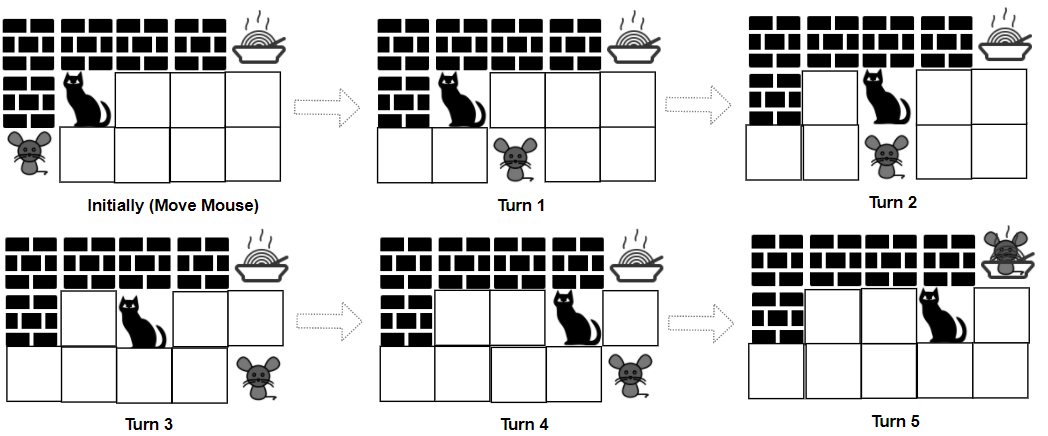
Input: grid = ["####F","#C...","M...."], catJump = 1, mouseJump = 2
Output: true
Explanation: Cat cannot catch Mouse on its turn nor can it get the food before Mouse.

Example 2

1
2

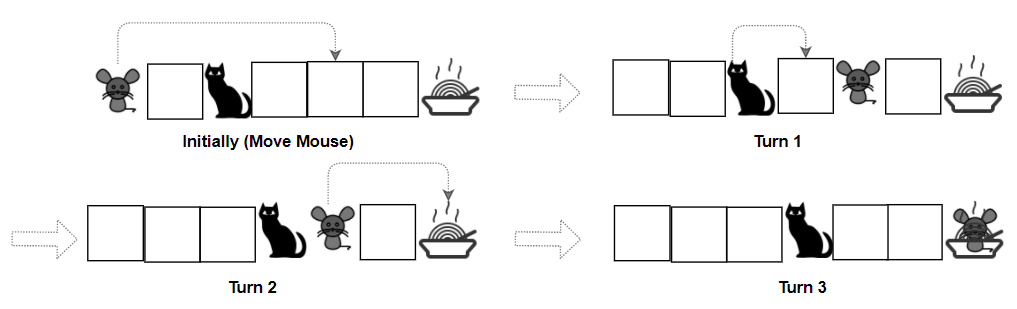
Input: grid = ["M.C...F"], catJump = 1, mouseJump = 4
Output: true

Example 3

1
2

Input: grid = ["M.C...F"], catJump = 1, mouseJump = 3
Output: false

Constraints

  • rows == grid.length
  • cols = grid[i].length

Solution

Method 1 – Game Theory with DFS and Memoization

Intuition: This is a two-player perfect information game. Each state is defined by the positions of the mouse and cat, whose turn it is, and the number of turns taken. The mouse wins if it reaches the food before the cat or before 1000 turns; the cat wins if it catches the mouse or reaches the food first. We use DFS to explore all possible moves and memoization to avoid recalculating the same state.

Approach:

  1. Parse the grid to find the initial positions of the mouse, cat, and food.
  2. Use DFS with memoization to simulate all possible moves for both players.
  3. For each state, check for base cases:
    • Cat catches mouse (same cell): Cat wins.
    • Cat reaches food: Cat wins.
    • Mouse reaches food: Mouse wins.
    • More than 1000 moves: Cat wins.
  4. For each move, try all possible jump distances in four directions, including staying in place.
  5. Alternate turns and recursively check if the current player can force a win.
  6. Memoize results for each state to avoid recomputation.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

class Solution {
public:
    int n, m, fR, fC, mR, mC, cR, cC;
    vector<string> g;
    int cJ, mJ;
    int dp[8][8][8][8][2][1001];
    bool canWin(int mr, int mc, int cr, int cc, int turn, int moves) {
        if (moves > 1000) return false;
        if (mr == cr && mc == cc) return false;
        if (cr == fR && cc == fC) return false;
        if (mr == fR && mc == fC) return true;
        int &res = dp[mr][mc][cr][cc][turn][moves];
        if (res != -1) return res;
        if (turn == 0) { // Mouse
            for (int d = 0; d < 5; ++d) {
                for (int j = 0; j <= mJ; ++j) {
                    int nr = mr, nc = mc;
                    if (d == 0) nr -= j;
                    if (d == 1) nr += j;
                    if (d == 2) nc -= j;
                    if (d == 3) nc += j;
                    if (nr < 0 || nr >= n || nc < 0 || nc >= m || g[nr][nc] == '#') break;
                    if (canWin(nr, nc, cr, cc, 1, moves + 1)) return res = 1;
                }
            }
            return res = 0;
        } else { // Cat
            for (int d = 0; d < 5; ++d) {
                for (int j = 0; j <= cJ; ++j) {
                    int nr = cr, nc = cc;
                    if (d == 0) nr -= j;
                    if (d == 1) nr += j;
                    if (d == 2) nc -= j;
                    if (d == 3) nc += j;
                    if (nr < 0 || nr >= n || nc < 0 || nc >= m || g[nr][nc] == '#') break;
                    if (!canWin(mr, mc, nr, nc, 0, moves + 1)) return res = 0;
                }
            }
            return res = 1;
        }
    }
    bool canMouseWin(vector<string>& grid, int catJump, int mouseJump) {
        n = grid.size(); m = grid[0].size(); g = grid; cJ = catJump; mJ = mouseJump;
        memset(dp, -1, sizeof(dp));
        for (int i = 0; i < n; ++i) for (int j = 0; j < m; ++j) {
            if (grid[i][j] == 'F') fR = i, fC = j;
            if (grid[i][j] == 'M') mR = i, mC = j;
            if (grid[i][j] == 'C') cR = i, cC = j;
        }
        return canWin(mR, mC, cR, cC, 0, 0);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

type state struct{mr,mc,cr,cc,turn,moves int}
func canMouseWin(grid []string, catJump, mouseJump int) bool {
    n, m := len(grid), len(grid[0])
    var fR, fC, mR, mC, cR, cC int
    for i := 0; i < n; i++ {
        for j := 0; j < m; j++ {
            if grid[i][j] == 'F' { fR, fC = i, j }
            if grid[i][j] == 'M' { mR, mC = i, j }
            if grid[i][j] == 'C' { cR, cC = i, j }
        }
    }
    memo := map[state]bool{}
    var dfs func(mr,mc,cr,cc,turn,moves int) bool
    dfs = func(mr,mc,cr,cc,turn,moves int) bool {
        if moves > 1000 { return false }
        if mr == cr && mc == cc { return false }
        if cr == fR && cc == fC { return false }
        if mr == fR && mc == fC { return true }
        key := state{mr,mc,cr,cc,turn,moves}
        if v, ok := memo[key]; ok { return v }
        if turn == 0 {
            for d := 0; d < 5; d++ {
                for j := 0; j <= mouseJump; j++ {
                    nr, nc := mr, mc
                    if d == 0 { nr -= j }
                    if d == 1 { nr += j }
                    if d == 2 { nc -= j }
                    if d == 3 { nc += j }
                    if nr < 0 || nr >= n || nc < 0 || nc >= m || grid[nr][nc] == '#' { break }
                    if dfs(nr, nc, cr, cc, 1, moves+1) { memo[key] = true; return true }
                }
            }
            memo[key] = false; return false
        } else {
            for d := 0; d < 5; d++ {
                for j := 0; j <= catJump; j++ {
                    nr, nc := cr, cc
                    if d == 0 { nr -= j }
                    if d == 1 { nr += j }
                    if d == 2 { nc -= j }
                    if d == 3 { nc += j }
                    if nr < 0 || nr >= n || nc < 0 || nc >= m || grid[nr][nc] == '#' { break }
                    if !dfs(mr, mc, nr, nc, 0, moves+1) { memo[key] = false; return false }
                }
            }
            memo[key] = true; return true
        }
    }
    return dfs(mR, mC, cR, cC, 0, 0)
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

class Solution {
    int n, m, fR, fC, mR, mC, cR, cC;
    int[][][][][][] dp;
    String[] g;
    int cJ, mJ;
    boolean dfs(int mr, int mc, int cr, int cc, int turn, int moves) {
        if (moves > 1000) return false;
        if (mr == cr && mc == cc) return false;
        if (cr == fR && cc == fC) return false;
        if (mr == fR && mc == fC) return true;
        if (dp[mr][mc][cr][cc][turn][moves] != -1) return dp[mr][mc][cr][cc][turn][moves] == 1;
        if (turn == 0) {
            for (int d = 0; d < 5; d++) {
                for (int j = 0; j <= mJ; j++) {
                    int nr = mr, nc = mc;
                    if (d == 0) nr -= j;
                    if (d == 1) nr += j;
                    if (d == 2) nc -= j;
                    if (d == 3) nc += j;
                    if (nr < 0 || nr >= n || nc < 0 || nc >= m || g[nr].charAt(nc) == '#') break;
                    if (dfs(nr, nc, cr, cc, 1, moves + 1)) {
                        dp[mr][mc][cr][cc][turn][moves] = 1;
                        return true;
                    }
                }
            }
            dp[mr][mc][cr][cc][turn][moves] = 0;
            return false;
        } else {
            for (int d = 0; d < 5; d++) {
                for (int j = 0; j <= cJ; j++) {
                    int nr = cr, nc = cc;
                    if (d == 0) nr -= j;
                    if (d == 1) nr += j;
                    if (d == 2) nc -= j;
                    if (d == 3) nc += j;
                    if (nr < 0 || nr >= n || nc < 0 || nc >= m || g[nr].charAt(nc) == '#') break;
                    if (!dfs(mr, mc, nr, nc, 0, moves + 1)) {
                        dp[mr][mc][cr][cc][turn][moves] = 0;
                        return false;
                    }
                }
            }
            dp[mr][mc][cr][cc][turn][moves] = 1;
            return true;
        }
    }
    public boolean canMouseWin(String[] grid, int catJump, int mouseJump) {
        n = grid.length; m = grid[0].length(); g = grid; cJ = catJump; mJ = mouseJump;
        dp = new int[n][m][n][m][2][1001];
        for (int[][][][][] a : dp) for (int[][][][] b : a) for (int[][][] c : b) for (int[][] d : c) for (int[] e : d) Arrays.fill(e, -1);
        for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) {
            if (grid[i].charAt(j) == 'F') { fR = i; fC = j; }
            if (grid[i].charAt(j) == 'M') { mR = i; mC = j; }
            if (grid[i].charAt(j) == 'C') { cR = i; cC = j; }
        }
        return dfs(mR, mC, cR, cC, 0, 0);
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

class Solution {
    lateinit var g: Array<String>
    var n = 0; var m = 0; var fR = 0; var fC = 0; var mR = 0; var mC = 0; var cR = 0; var cC = 0
    lateinit var dp: Array<Array<Array<Array<Array<Array<Int>>>>>>
    var cJ = 0; var mJ = 0
    fun dfs(mr: Int, mc: Int, cr: Int, cc: Int, turn: Int, moves: Int): Boolean {
        if (moves > 1000) return false
        if (mr == cr && mc == cc) return false
        if (cr == fR && cc == fC) return false
        if (mr == fR && mc == fC) return true
        if (dp[mr][mc][cr][cc][turn][moves] != -1) return dp[mr][mc][cr][cc][turn][moves] == 1
        if (turn == 0) {
            for (d in 0..4) {
                for (j in 0..mJ) {
                    var nr = mr; var nc = mc
                    if (d == 0) nr -= j
                    if (d == 1) nr += j
                    if (d == 2) nc -= j
                    if (d == 3) nc += j
                    if (nr < 0 || nr >= n || nc < 0 || nc >= m || g[nr][nc] == '#') break
                    if (dfs(nr, nc, cr, cc, 1, moves + 1)) {
                        dp[mr][mc][cr][cc][turn][moves] = 1
                        return true
                    }
                }
            }
            dp[mr][mc][cr][cc][turn][moves] = 0
            return false
        } else {
            for (d in 0..4) {
                for (j in 0..cJ) {
                    var nr = cr; var nc = cc
                    if (d == 0) nr -= j
                    if (d == 1) nr += j
                    if (d == 2) nc -= j
                    if (d == 3) nc += j
                    if (nr < 0 || nr >= n || nc < 0 || nc >= m || g[nr][nc] == '#') break
                    if (!dfs(mr, mc, nr, nc, 0, moves + 1)) {
                        dp[mr][mc][cr][cc][turn][moves] = 0
                        return false
                    }
                }
            }
            dp[mr][mc][cr][cc][turn][moves] = 1
            return true
        }
    }
    fun canMouseWin(grid: Array<String>, catJump: Int, mouseJump: Int): Boolean {
        n = grid.size; m = grid[0].length; g = grid; cJ = catJump; mJ = mouseJump
        dp = Array(n) { Array(m) { Array(n) { Array(m) { Array(2) { Array(1001) { -1 } } } } } }
        for (i in 0 until n) for (j in 0 until m) {
            if (grid[i][j] == 'F') { fR = i; fC = j }
            if (grid[i][j] == 'M') { mR = i; mC = j }
            if (grid[i][j] == 'C') { cR = i; cC = j }
        }
        return dfs(mR, mC, cR, cC, 0, 0)
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution:
    def canMouseWin(self, grid: list[str], catJump: int, mouseJump: int) -> bool:
        n, m = len(grid), len(grid[0])
        for i in range(n):
            for j in range(m):
                if grid[i][j] == 'F': fR, fC = i, j
                if grid[i][j] == 'M': mR, mC = i, j
                if grid[i][j] == 'C': cR, cC = i, j
        from functools import lru_cache
        @lru_cache(None)
        def dfs(mr: int, mc: int, cr: int, cc: int, turn: int, moves: int) -> bool:
            if moves > 1000: return False
            if mr == cr and mc == cc: return False
            if cr == fR and cc == fC: return False
            if mr == fR and mc == fC: return True
            if turn == 0:
                for d in range(5):
                    for j in range(mouseJump+1):
                        nr, nc = mr, mc
                        if d == 0: nr -= j
                        if d == 1: nr += j
                        if d == 2: nc -= j
                        if d == 3: nc += j
                        if nr < 0 or nr >= n or nc < 0 or nc >= m or grid[nr][nc] == '#': break
                        if dfs(nr, nc, cr, cc, 1, moves + 1): return True
            else:
                for d in range(5):
                    for j in range(catJump+1):
                        nr, nc = cr, cc
                        if d == 0: nr -= j
                        if d == 1: nr += j
                        if d == 2: nc -= j
                        if d == 3: nc += j
                        if nr < 0 or nr >= n or nc < 0 or nc >= m or grid[nr][nc] == '#': break
                        if not dfs(mr, mc, nr, nc, 0, moves + 1): return False
            return True if turn == 0 else False
        return dfs(mR, mC, cR, cC, 0, 0)

Complexity

  • ⏰ Time complexity: O(n^5), where n is the number of cells (due to positions and turn count).
  • 🧺 Space complexity: O(n^5) for memoization.