problemmediumalgorithmsleetcode-1430leetcode 1430leetcode1430

Check If a String Is a Valid Sequence from Root to Leaves Path in a Binary Tree

MediumUpdated: Jul 3, 2025
Practice on:
LeetCode

Problem

Given a binary tree where each path going from the root to any leaf form a valid sequence , check if a given string is a valid sequence in such binary tree.

We get the given string from the concatenation of an array of integers arr and the concatenation of all values of the nodes along a path results in a sequence in the given binary tree.

Examples

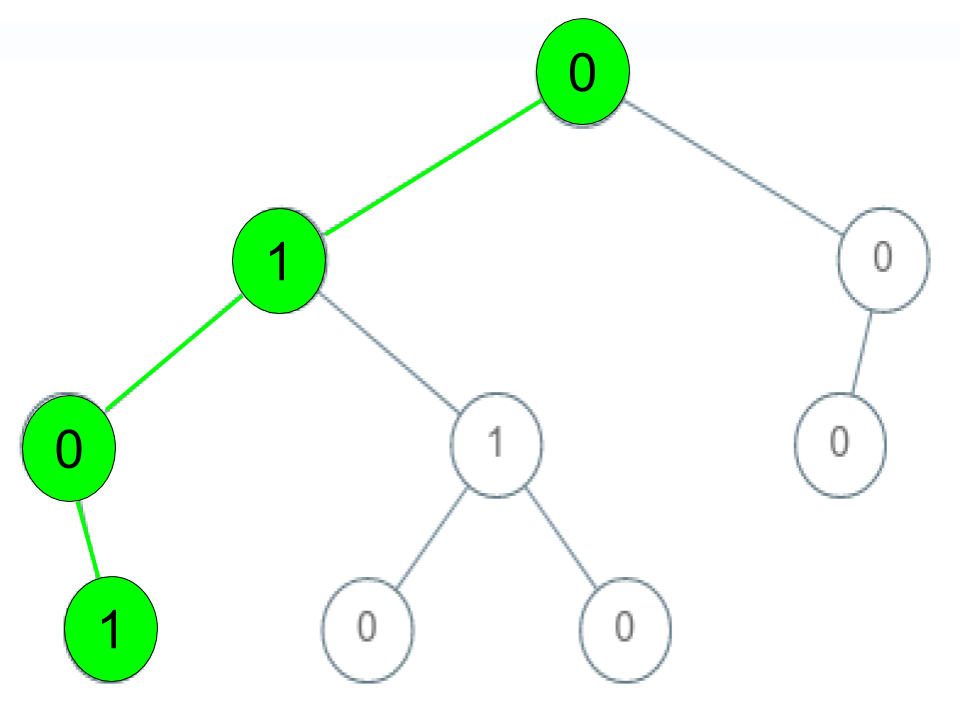Example 1:

Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,0,1]
Output: true
Explanation: The path 0 -> 1 -> 0 -> 1 is a valid sequence (green color in the figure). 
Other valid sequences are: 
0 -> 1 -> 1 -> 0 
0 -> 0 -> 0

Example 2: 

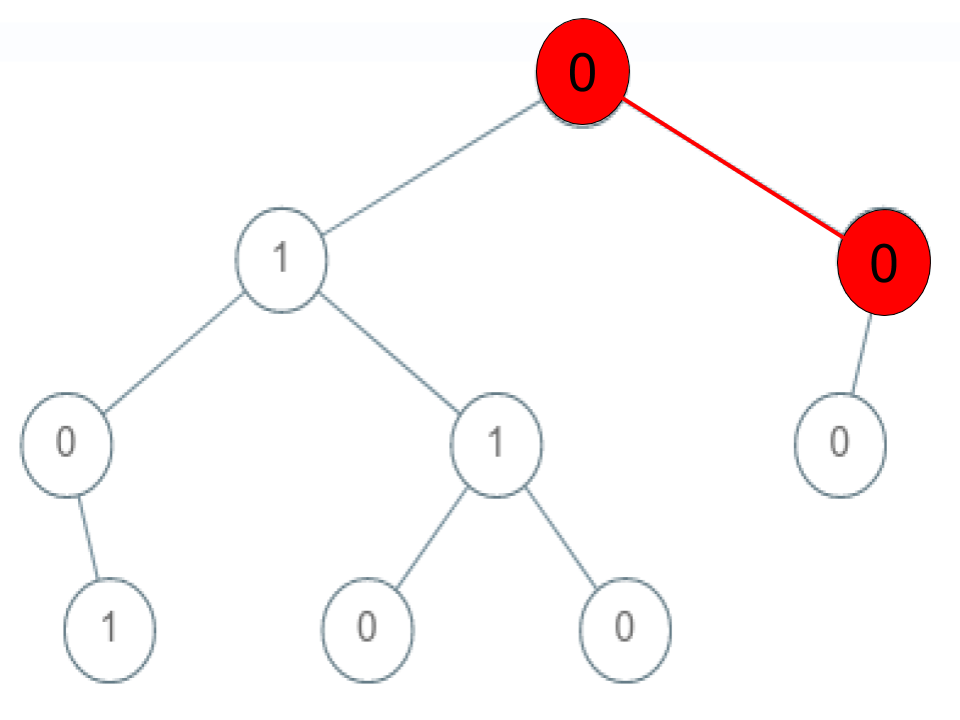
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,0,1]
Output: false 
Explanation: The path 0 -> 0 -> 1 does not exist, therefore it is not even a sequence.

Example 3: 

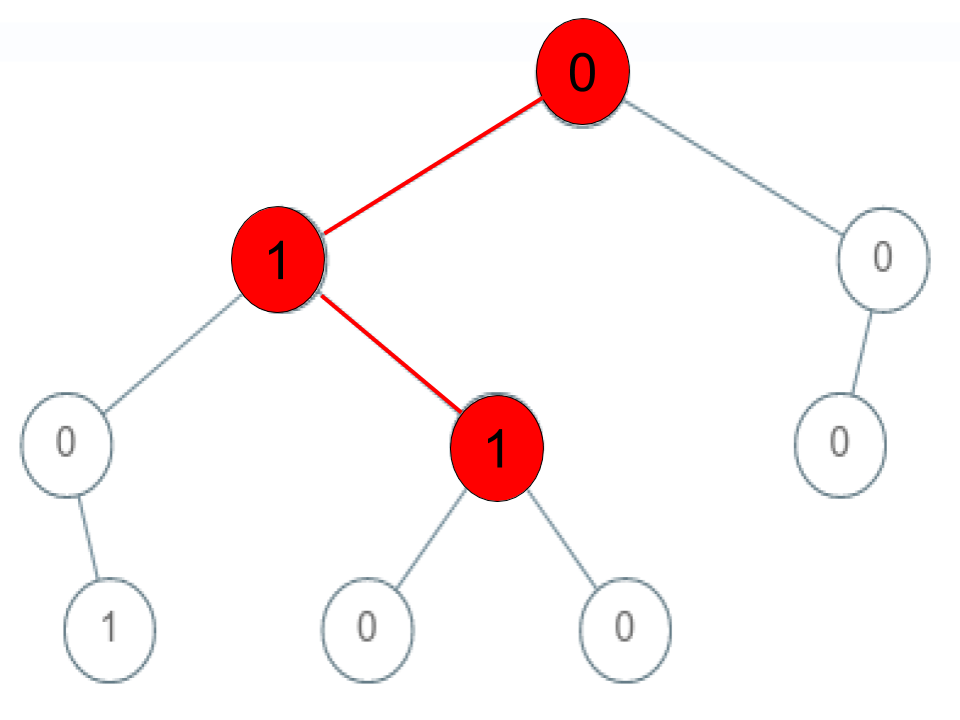
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,1]
Output: false
Explanation: The path 0 -> 1 -> 1 is a sequence, but it is not a valid sequence.

Constraints:

  • 1 <= arr.length <= 5000
  • 0 <= arr[i] <= 9
  • Each node's value is between [0 - 9].

Solution

Method 1 – Depth-First Search (DFS) Path Matching

Intuition

We need to check if there exists a root-to-leaf path in the binary tree such that the sequence of node values matches the given array. This is a classic DFS problem where we match the current node's value with the current index in the array and recursively check the left and right subtrees.

Approach

  1. Start DFS from the root node and index 0 of the array.
  2. At each node:
    • If the node is null or the index is out of bounds, return false.
    • If the node's value does not match arr[index], return false.
    • If at a leaf node and index is at the last element of arr, return true.
    • Recursively check left and right children with index + 1.
  3. Return true if any path matches, else false.

Code

C++
class Solution {
public:
    bool isValidSequence(TreeNode* root, vector<int>& arr) {
        return dfs(root, arr, 0);
    }
    bool dfs(TreeNode* node, vector<int>& arr, int idx) {
        if (!node || idx >= arr.size() || node->val != arr[idx]) return false;
        if (!node->left && !node->right && idx == arr.size() - 1) return true;
        return dfs(node->left, arr, idx + 1) || dfs(node->right, arr, idx + 1);
    }
};
Go
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func isValidSequence(root *TreeNode, arr []int) bool {
    var dfs func(node *TreeNode, idx int) bool
    dfs = func(node *TreeNode, idx int) bool {
        if node == nil || idx >= len(arr) || node.Val != arr[idx] {
            return false
        }
        if node.Left == nil && node.Right == nil && idx == len(arr)-1 {
            return true
        }
        return dfs(node.Left, idx+1) || dfs(node.Right, idx+1)
    }
    return dfs(root, 0)
}
Java
class Solution {
    public boolean isValidSequence(TreeNode root, int[] arr) {
        return dfs(root, arr, 0);
    }
    private boolean dfs(TreeNode node, int[] arr, int idx) {
        if (node == null || idx >= arr.length || node.val != arr[idx]) return false;
        if (node.left == null && node.right == null && idx == arr.length - 1) return true;
        return dfs(node.left, arr, idx + 1) || dfs(node.right, arr, idx + 1);
    }
}
Kotlin
class Solution {
    fun isValidSequence(root: TreeNode?, arr: IntArray): Boolean {
        fun dfs(node: TreeNode?, idx: Int): Boolean {
            if (node == null || idx >= arr.size || node.`val` != arr[idx]) return false
            if (node.left == null && node.right == null && idx == arr.size - 1) return true
            return dfs(node.left, idx + 1) || dfs(node.right, idx + 1)
        }
        return dfs(root, 0)
    }
}
Python
class Solution:
    def isValidSequence(self, root: 'TreeNode', arr: list[int]) -> bool:
        def dfs(node: 'TreeNode', idx: int) -> bool:
            if not node or idx >= len(arr) or node.val != arr[idx]:
                return False
            if not node.left and not node.right and idx == len(arr) - 1:
                return True
            return dfs(node.left, idx + 1) or dfs(node.right, idx + 1)
        return dfs(root, 0)
Rust
impl Solution {
    pub fn is_valid_sequence(root: Option<Rc<RefCell<TreeNode>>>, arr: Vec<i32>) -> bool {
        fn dfs(node: Option<Rc<RefCell<TreeNode>>>, arr: &Vec<i32>, idx: usize) -> bool {
            if node.is_none() || idx >= arr.len() { return false; }
            let n = node.as_ref().unwrap().borrow();
            if n.val != arr[idx] { return false; }
            if n.left.is_none() && n.right.is_none() && idx == arr.len() - 1 { return true; }
            dfs(n.left.clone(), arr, idx + 1) || dfs(n.right.clone(), arr, idx + 1)
        }
        dfs(root, &arr, 0)
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes in the tree.
  • 🧺 Space complexity: O(h), where h is the height of the tree (recursion stack).

Comments