problemeasyalgorithmsleetcode-1437leetcode 1437leetcode1437

Check If All 1's Are at Least Length K Places Away

EasyUpdated: Jul 3, 2025
Practice on:
LeetCode

Problem

Given an binary array nums and an integer k, return true if all1 _' s are at least _k places away from each other, otherwise returnfalse.

Examples

Example 1

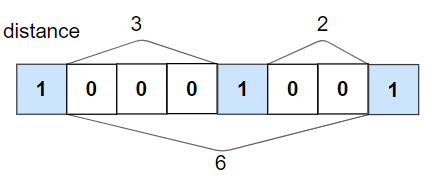
Input: nums = [1,0,0,0,1,0,0,1], k = 2
Output: true
Explanation: Each of the 1s are at least 2 places away from each other.

Example 2

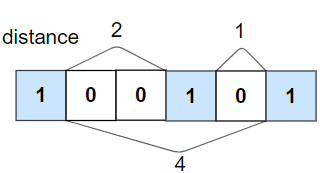
Input: nums = [1,0,0,1,0,1], k = 2
Output: false
Explanation: The second 1 and third 1 are only one apart from each other.

Constraints

  • 1 <= nums.length <= 10^5
  • 0 <= k <= nums.length
  • nums[i] is 0 or 1

Solution

Method 1 – Greedy Distance Tracking

Intuition

The main idea is to track the position of the last seen 1. For each new 1, check if the distance from the previous 1 is at least k. If not, return false. This works because the only way to violate the rule is to have two 1's too close together.

Approach

  1. Initialize a variable to store the index of the last seen 1 (set to -k-1 initially).
  2. Iterate through the array:
    • If the current element is 1:
      • Check if the distance from the last 1 is less than or equal to k.
      • If so, return false.
      • Update the last seen 1 index.
  3. If the loop completes, return true.

Code

C++
class Solution {
public:
    bool kLengthApart(vector<int>& nums, int k) {
        int last = -k-1;
        for (int i = 0; i < nums.size(); ++i) {
            if (nums[i] == 1) {
                if (i - last <= k) return false;
                last = i;
            }
        }
        return true;
    }
};
Go
func kLengthApart(nums []int, k int) bool {
    last := -k-1
    for i, v := range nums {
        if v == 1 {
            if i - last <= k {
                return false
            }
            last = i
        }
    }
    return true
}
Java
class Solution {
    public boolean kLengthApart(int[] nums, int k) {
        int last = -k-1;
        for (int i = 0; i < nums.length; ++i) {
            if (nums[i] == 1) {
                if (i - last <= k) return false;
                last = i;
            }
        }
        return true;
    }
}
Kotlin
class Solution {
    fun kLengthApart(nums: IntArray, k: Int): Boolean {
        var last = -k-1
        for (i in nums.indices) {
            if (nums[i] == 1) {
                if (i - last <= k) return false
                last = i
            }
        }
        return true
    }
}
Python
def kLengthApart(nums: list[int], k: int) -> bool:
    last: int = -k-1
    for i, v in enumerate(nums):
        if v == 1:
            if i - last <= k:
                return False
            last = i
    return True
Rust
impl Solution {
    pub fn k_length_apart(nums: Vec<i32>, k: i32) -> bool {
        let mut last = -k - 1;
        for (i, &v) in nums.iter().enumerate() {
            if v == 1 {
                if (i as i32) - last <= k {
                    return false;
                }
                last = i as i32;
            }
        }
        true
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the length of the array.
  • 🧺 Space complexity: O(1).

Comments