Check if DFS Strings Are Palindromes

Problem

You are given a tree rooted at node 0, consisting of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

Consider an empty string dfsStr, and define a recursive function dfs(int x) that takes a node x as a parameter and performs the following steps in order:

• Iterate over each child y of x in increasing order of their numbers , and call dfs(y).
• Add the character s[x] to the end of the string dfsStr.

Note that dfsStr is shared across all recursive calls of dfs.

You need to find a boolean array answer of size n, where for each index i from 0 to n - 1, you do the following:

• Empty the string dfsStr and call dfs(i).
• If the resulting string dfsStr is a palindrome, then set answer[i] to true. Otherwise, set answer[i] to false.

Return the array answer.

Examples

Example 1

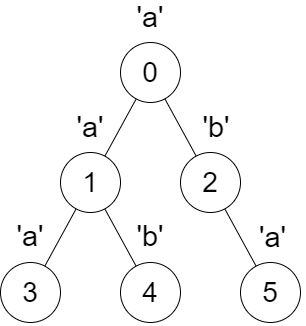
Input: parent = [-1,0,0,1,1,2], s = "aababa"
Output: [true,true,false,true,true,true]
Explanation:
  * Calling `dfs(0)` results in the string `dfsStr = "abaaba"`, which is a palindrome.
  * Calling `dfs(1)` results in the string `dfsStr = "aba"`, which is a palindrome.
  * Calling `dfs(2)` results in the string `dfsStr = "ab"`, which is **not** a palindrome.
  * Calling `dfs(3)` results in the string `dfsStr = "a"`, which is a palindrome.
  * Calling `dfs(4)` results in the string `dfsStr = "b"`, which is a palindrome.
  * Calling `dfs(5)` results in the string `dfsStr = "a"`, which is a palindrome.

Example 2

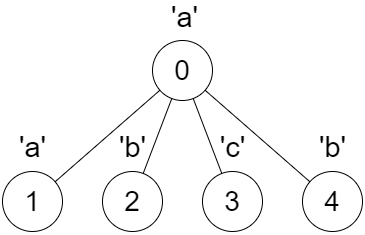
Input: parent = [-1,0,0,0,0], s = "aabcb"
Output: [true,true,true,true,true]
Explanation:
Every call on `dfs(x)` results in a palindrome string.

Constraints

• n == parent.length == s.length
• 1 <= n <= 10^5
• 0 <= parent[i] <= n - 1 for all i >= 1.
• parent[0] == -1
• parent represents a valid tree.
• s consists only of lowercase English letters.

Solution

Method 1 – DFS with String Construction

Intuition

The key idea is to simulate the DFS as described, building the string for each subtree rooted at every node, and then check if the resulting string is a palindrome. Since the tree can be large, we need to be careful with string operations, but for each node, we can construct the string by traversing its subtree in postorder.

Approach

1. Build the tree as an adjacency list from the parent array.
2. For each node i from 0 to n-1:
   • Start a DFS from node i, traversing children in increasing order.
   • Build the string as per the problem's DFS order.
   • Check if the string is a palindrome.
   • Store the result in the answer array.
3. Return the answer array.

Edge cases:

• Single node: always a palindrome.
• All nodes with the same character: always palindromes.

Code

C++

class Solution {
public:
    vector<bool> checkPalindromeDFS(vector<int>& parent, string s) {
        int n = parent.size();
        vector<vector<int>> g(n);
        for (int i = 1; i < n; ++i) g[parent[i]].push_back(i);
        for (auto& v : g) sort(v.begin(), v.end());
        vector<bool> ans(n);
        function<void(int, string&)> dfs = [&](int u, string& t) {
            for (int v : g[u]) dfs(v, t);
            t += s[u];
        };
        for (int i = 0; i < n; ++i) {
            string t;
            dfs(i, t);
            ans[i] = equal(t.begin(), t.begin() + t.size()/2, t.rbegin());
        }
        return ans;
    }
};

Go

func checkPalindromeDFS(parent []int, s string) []bool {
    n := len(parent)
    g := make([][]int, n)
    for i := 1; i < n; i++ {
        g[parent[i]] = append(g[parent[i]], i)
    }
    for i := range g {
        sort.Ints(g[i])
    }
    ans := make([]bool, n)
    var dfs func(int, *[]byte)
    dfs = func(u int, t *[]byte) {
        for _, v := range g[u] {
            dfs(v, t)
        }
        *t = append(*t, s[u])
    }
    for i := 0; i < n; i++ {
        t := []byte{}
        dfs(i, &t)
        ok := true
        for l, r := 0, len(t)-1; l < r; l, r = l+1, r-1 {
            if t[l] != t[r] {
                ok = false
                break
            }
        }
        ans[i] = ok
    }
    return ans
}

Java

class Solution {
    public List<Boolean> checkPalindromeDFS(int[] parent, String s) {
        int n = parent.length;
        List<Integer>[] g = new ArrayList[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int i = 1; i < n; i++) g[parent[i]].add(i);
        for (List<Integer> v : g) Collections.sort(v);
        List<Boolean> ans = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            StringBuilder t = new StringBuilder();
            dfs(i, g, s, t);
            ans.add(isPalindrome(t));
        }
        return ans;
    }
    void dfs(int u, List<Integer>[] g, String s, StringBuilder t) {
        for (int v : g[u]) dfs(v, g, s, t);
        t.append(s.charAt(u));
    }
    boolean isPalindrome(StringBuilder t) {
        int l = 0, r = t.length() - 1;
        while (l < r) if (t.charAt(l++) != t.charAt(r--)) return false;
        return true;
    }
}

Kotlin

class Solution {
    fun checkPalindromeDFS(parent: IntArray, s: String): List<Boolean> {
        val n = parent.size
        val g = Array(n) { mutableListOf<Int>() }
        for (i in 1 until n) g[parent[i]].add(i)
        g.forEach { it.sort() }
        val ans = MutableList(n) { false }
        fun dfs(u: Int, t: StringBuilder) {
            for (v in g[u]) dfs(v, t)
            t.append(s[u])
        }
        for (i in 0 until n) {
            val t = StringBuilder()
            dfs(i, t)
            ans[i] = t.toString() == t.reverse().toString()
        }
        return ans
    }
}

Python

class Solution:
    def check_palindrome_dfs(self, parent: list[int], s: str) -> list[bool]:
        n = len(parent)
        g: list[list[int]] = [[] for _ in range(n)]
        for i in range(1, n):
            g[parent[i]].append(i)
        for v in g:
            v.sort()
        def dfs(u: int, t: list[str]):
            for v in g[u]:
                dfs(v, t)
            t.append(s[u])
        ans: list[bool] = []
        for i in range(n):
            t: list[str] = []
            dfs(i, t)
            ans.append(t == t[::-1])
        return ans

Rust

impl Solution {
    pub fn check_palindrome_dfs(parent: Vec<i32>, s: String) -> Vec<bool> {
        let n = parent.len();
        let mut g = vec![vec![]; n];
        for i in 1..n {
            g[parent[i] as usize].push(i);
        }
        for v in &mut g {
            v.sort();
        }
        let s = s.as_bytes();
        let mut ans = vec![false; n];
        fn dfs(u: usize, g: &Vec<Vec<usize>>, s: &[u8], t: &mut Vec<u8>) {
            for &v in &g[u] {
                dfs(v, g, s, t);
            }
            t.push(s[u]);
        }
        for i in 0..n {
            let mut t = vec![];
            dfs(i, &g, s, &mut t);
            ans[i] = t.iter().eq(t.iter().rev());
        }
        ans
    }
}

Complexity

• ⏰ Time complexity: O(n^2), as for each node, we perform a DFS to collect all characters in its subtree, which can take up to O(n) time per node in the worst case (e.g., a skewed tree). Since we do this for every node, the total time is O(n^2).
• 🧺 Space complexity: O(n^2), as we may construct a string of up to O(n) size for each node, and since we do this for all n nodes, the total auxiliary space can reach O(n^2) in the worst case.