problemeasyalgorithmsleetcode-2133leetcode 2133leetcode2133

Check if Every Row and Column Contains All Numbers

EasyUpdated: Jul 4, 2025
Practice on:
LeetCode

Problem

An n x n matrix is valid if every row and every column contains all the integers from 1 to n (inclusive).

Given an n x n integer matrix matrix, return true if the matrix isvalid. Otherwise, return false.

Examples

Example 1

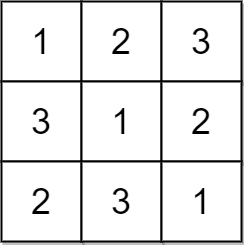
Input: matrix = [[1,2,3],[3,1,2],[2,3,1]]
Output: true
Explanation: In this case, n = 3, and every row and column contains the numbers 1, 2, and 3.
Hence, we return true.

Example 2

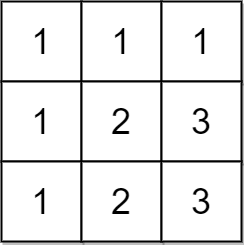
Input: matrix = [[1,1,1],[1,2,3],[1,2,3]]
Output: false
Explanation: In this case, n = 3, but the first row and the first column do not contain the numbers 2 or 3.
Hence, we return false.

Constraints

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 100
  • 1 <= matrix[i][j] <= n

Solution

Method 1 – Frequency Set Check

Intuition

Each row and each column must contain all numbers from 1 to n exactly once. We can check this by verifying that the set of numbers in each row and each column matches the set {1, 2, ..., n}.

Approach

  1. Let n be the size of the matrix.
  2. For each row, check if the set of its elements is equal to {1, 2, ..., n}.
  3. For each column, check if the set of its elements is equal to {1, 2, ..., n}.
  4. If all rows and columns pass the check, return true; otherwise, return false.

Code

C++
class Solution {
public:
    bool checkValid(vector<vector<int>>& matrix) {
        int n = matrix.size();
        unordered_set<int> expected;
        for (int i = 1; i <= n; ++i) expected.insert(i);
        for (int i = 0; i < n; ++i) {
            unordered_set<int> row, col;
            for (int j = 0; j < n; ++j) {
                row.insert(matrix[i][j]);
                col.insert(matrix[j][i]);
            }
            if (row != expected || col != expected) return false;
        }
        return true;
    }
};
Go
func checkValid(matrix [][]int) bool {
    n := len(matrix)
    expected := make(map[int]struct{}, n)
    for i := 1; i <= n; i++ { expected[i] = struct{}{} }
    for i := 0; i < n; i++ {
        row := make(map[int]struct{}, n)
        col := make(map[int]struct{}, n)
        for j := 0; j < n; j++ {
            row[matrix[i][j]] = struct{}{}
            col[matrix[j][i]] = struct{}{}
        }
        if len(row) != n || len(col) != n {
            return false
        }
        for k := range expected {
            if _, ok := row[k]; !ok { return false }
            if _, ok := col[k]; !ok { return false }
        }
    }
    return true
}
Java
class Solution {
    public boolean checkValid(int[][] matrix) {
        int n = matrix.length;
        Set<Integer> expected = new HashSet<>();
        for (int i = 1; i <= n; ++i) expected.add(i);
        for (int i = 0; i < n; ++i) {
            Set<Integer> row = new HashSet<>();
            Set<Integer> col = new HashSet<>();
            for (int j = 0; j < n; ++j) {
                row.add(matrix[i][j]);
                col.add(matrix[j][i]);
            }
            if (!row.equals(expected) || !col.equals(expected)) return false;
        }
        return true;
    }
}
Kotlin
class Solution {
    fun checkValid(matrix: Array<IntArray>): Boolean {
        val n = matrix.size
        val expected = (1..n).toSet()
        for (i in 0 until n) {
            val row = mutableSetOf<Int>()
            val col = mutableSetOf<Int>()
            for (j in 0 until n) {
                row.add(matrix[i][j])
                col.add(matrix[j][i])
            }
            if (row != expected || col != expected) return false
        }
        return true
    }
}
Python
class Solution:
    def checkValid(self, matrix: list[list[int]]) -> bool:
        n = len(matrix)
        expected = set(range(1, n+1))
        for i in range(n):
            if set(matrix[i]) != expected:
                return False
            if set(matrix[j][i] for j in range(n)) != expected:
                return False
        return True
Rust
use std::collections::HashSet;
impl Solution {
    pub fn check_valid(matrix: Vec<Vec<i32>>) -> bool {
        let n = matrix.len();
        let expected: HashSet<i32> = (1..=n as i32).collect();
        for i in 0..n {
            let row: HashSet<i32> = matrix[i].iter().cloned().collect();
            let col: HashSet<i32> = (0..n).map(|j| matrix[j][i]).collect();
            if row != expected || col != expected { return false; }
        }
        true
    }
}

Complexity

  • ⏰ Time complexity: O(n^2), where n is the size of the matrix.
  • 🧺 Space complexity: O(n)

Comments