problemmediumalgorithmsleetcode-3394leetcode 3394leetcode3394

Check if Grid can be Cut into Sections

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an integer n representing the dimensions of an n x n grid, with the origin at the bottom-left corner of the grid. You are also given a 2D array of coordinates rectangles, where rectangles[i] is in the form [startx, starty, endx, endy], representing a rectangle on the grid. Each rectangle is defined as follows:

  • (startx, starty): The bottom-left corner of the rectangle.
  • (endx, endy): The top-right corner of the rectangle.

Note that the rectangles do not overlap. Your task is to determine if it is possible to make either two horizontal or two vertical cuts on the grid such that:

  • Each of the three resulting sections formed by the cuts contains at least one rectangle.
  • Every rectangle belongs to exactly one section.

Return true if such cuts can be made; otherwise, return false.

Examples

Example 1

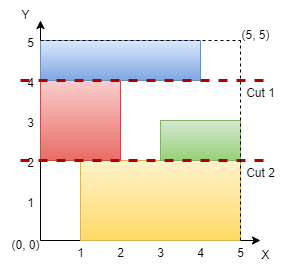
Input: n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
Output: true
Explanation:
The grid is shown in the diagram. We can make horizontal cuts at `y = 2` and `y = 4`. Hence, output is true.

Example 2

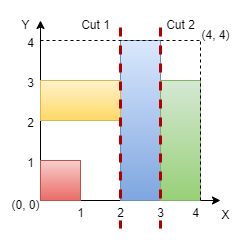
Input: n = 4, rectangles = [[0,0,1,1],[2,0,3,4],[0,2,2,3],[3,0,4,3]]
Output: true
Explanation:
We can make vertical cuts at `x = 2` and `x = 3`. Hence, output is true.

Example 3

Input: n = 4, rectangles = [[0,2,2,4],[1,0,3,2],[2,2,3,4],[3,0,4,2],[3,2,4,4]]
Output: false
Explanation:
We cannot make two horizontal or two vertical cuts that satisfy the conditions. Hence, output is false.

Solution

Method 1 - Sorting

  1. Extract Intervals:

    • The rectangles represent intervals on either the x-axis (horizontal intervals) or y-axis (vertical intervals).
    • We extract these intervals (x_bounds for the x-axis and y_bounds for the y-axis) to handle the problem separately for horizontal and vertical cuts.

  2. Sort Intervals:

    • The intervals are sorted based on their starting coordinates (interval[0]). This helps us in efficiently determining sections.

  3. Count Sections:

    • After sorting, iterate through the intervals to check where a new section starts. A new section begins when the current interval starts after the maximum boundary of the previous intervals.
    • For each section, update the max_boundary to track the farthest end of the current section.

  4. Validation:

    • If at least two sections are formed (section_count >= 2), it implies valid cuts are possible to divide the rectangles correctly, and we return True.

  5. Final Result:

    • The method checks both x-axis and y-axis cuts independently to determine validity. If either axis has valid cuts, the result is True.

Code

Java
class Solution {
    public boolean checkValidCuts(int n, int[][] rectangles) {
        int m = rectangles.length;
        // Extract intervals for x-axis and y-axis
        int[][] xBounds = new int[m][2];
        int[][] yBounds = new int[m][2];

        // Populate the bounds arrays
        for (int i = 0; i < m; i++) {
            xBounds[i][0] = rectangles[i][0]; // Start x-coordinate
            xBounds[i][1] = rectangles[i][2]; // End x-coordinate
            yBounds[i][0] = rectangles[i][1]; // Start y-coordinate
            yBounds[i][1] = rectangles[i][3]; // End y-coordinate
        }

        // Check for valid cuts on either axis
        return canFormSections(xBounds) || canFormSections(yBounds);
    }

    private boolean canFormSections(int[][] intervals) {
        // Sort intervals by their start values
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));

        int sectionCount = 0; // Start with one section
        int maxBoundary = intervals[0][1]; // Track the maximum boundary of the current section

        for (int[] interval : intervals) {
            if (maxBoundary <= interval[0]) {
                sectionCount++; // New section
            }
            maxBoundary = Math.max(maxBoundary, interval[1]); // Extend the current boundary
        }

        // Check if we can form at least three sections
        return sectionCount >= 2;
    }
}
Python
class Solution:
    def check_valid_cuts(self, n: int, rectangles: List[List[int]]) -> bool:
        m = len(rectangles)
        
        # Extract intervals for x-axis and y-axis
        x_bounds = [[rect[0], rect[2]] for rect in rectangles]
        y_bounds = [[rect[1], rect[3]] for rect in rectangles]
        
        # Check for valid cuts on either axis
        return self.can_form_sections(x_bounds) or self.can_form_sections(y_bounds)

    def can_form_sections(self, intervals: List[List[int]]) -> bool:
        # Sort intervals by their start values
        intervals.sort(key=lambda x: x[0])
        
        section_count = 0
        max_boundary = intervals[0][1]  # Track the maximum boundary of the current section

        for interval in intervals:
            if max_boundary <= interval[0]:
                section_count += 1  # New section
            max_boundary = max(max_boundary, interval[1])  # Extend the current boundary
        
        # Check if we can form at

Complexity

  • ⏰ Time complexity: O(m log m)
    • Interval extraction: O(m) (where m is the number of rectangles).
    • Sorting intervals: O(m log m).
    • Iterating intervals to check sections: O(m).
    • Overall: O(m log m), dominated by sorting.
  • 🧺 Space complexity: O(m)
    • Space for extracting intervals (x_bounds and y_bounds): O(m).
    • Space for sorting intermediate structures: O(m).
    • Overall: O(m), proportional to the number of rectangles.

Comments