Check if Grid Satisfies Conditions

Problem

You are given a 2D matrix grid of size m x n. You need to check if each cell grid[i][j] is:

• Equal to the cell below it, i.e. grid[i][j] == grid[i + 1][j] (if it exists).
• Different from the cell to its right, i.e. grid[i][j] != grid[i][j + 1] (if it exists).

Return true if all the cells satisfy these conditions, otherwise, return false.

Examples

Example 1

Input: grid = [[1,0,2],[1,0,2]]
Output: true

Explanation:

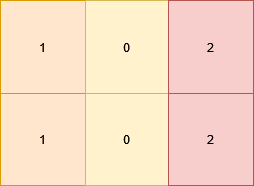
All the cells in the grid satisfy the conditions.

Example 2

Input: grid = [[1,1,1],[0,0,0]]
Output: false

Explanation:

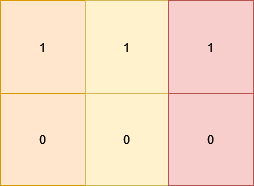
All cells in the first row are equal.

Example 3

Input: grid = [[1],[2],[3]]
Output: false

Explanation:

Cells in the first column have different values.

Constraints

• 1 <= n, m <= 10
• 0 <= grid[i][j] <= 9

Solution

Method 1 – Direct Grid Scan

Intuition

We need to check two conditions for each cell: (1) it is equal to the cell below (if it exists), and (2) it is different from the cell to its right (if it exists). We can scan the grid and check these conditions for every cell.

Approach

1. Let m and n be the number of rows and columns in the grid.
2. For each cell (i, j):
   • If i + 1 < m, check if grid[i][j] == grid[i+1][j]. If not, return false.
   • If j + 1 < n, check if grid[i][j] != grid[i][j+1]. If not, return false.
3. If all checks pass, return true.

Code

C++

class Solution {
public:
    bool satisfiesConditions(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i + 1 < m && grid[i][j] != grid[i+1][j]) return false;
                if (j + 1 < n && grid[i][j] == grid[i][j+1]) return false;
            }
        }
        return true;
    }
};

Go

func satisfiesConditions(grid [][]int) bool {
    m, n := len(grid), len(grid[0])
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if i+1 < m && grid[i][j] != grid[i+1][j] {
                return false
            }
            if j+1 < n && grid[i][j] == grid[i][j+1] {
                return false
            }
        }
    }
    return true
}

Java

class Solution {
    public boolean satisfiesConditions(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i + 1 < m && grid[i][j] != grid[i+1][j]) return false;
                if (j + 1 < n && grid[i][j] == grid[i][j+1]) return false;
            }
        }
        return true;
    }
}

Kotlin

class Solution {
    fun satisfiesConditions(grid: Array<IntArray>): Boolean {
        val m = grid.size
        val n = grid[0].size
        for (i in 0 until m) {
            for (j in 0 until n) {
                if (i + 1 < m && grid[i][j] != grid[i+1][j]) return false
                if (j + 1 < n && grid[i][j] == grid[i][j+1]) return false
            }
        }
        return true
    }
}

Python

class Solution:
    def satisfiesConditions(self, grid: list[list[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        for i in range(m):
            for j in range(n):
                if i + 1 < m and grid[i][j] != grid[i+1][j]:
                    return False
                if j + 1 < n and grid[i][j] == grid[i][j+1]:
                    return False
        return True

Rust

impl Solution {
    pub fn satisfies_conditions(grid: Vec<Vec<i32>>) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        for i in 0..m {
            for j in 0..n {
                if i + 1 < m && grid[i][j] != grid[i+1][j] {
                    return false;
                }
                if j + 1 < n && grid[i][j] == grid[i][j+1] {
                    return false;
                }
            }
        }
        true
    }
}

Complexity

• ⏰ Time complexity: O(mn), where m and n are the grid dimensions.
• 🧺 Space complexity: O(1)