problemeasyalgorithmsleetcode-1232leetcode 1232leetcode1232

Check If It Is a Straight Line

EasyUpdated: Jul 31, 2025
Practice on:
LeetCode

Problem

You are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.

Examples

Example 1:

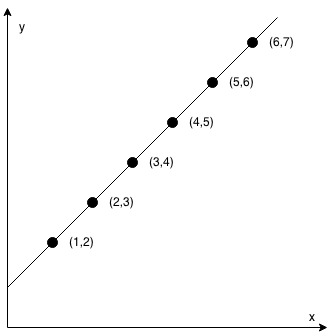
Input:
coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
Output:
 true

Example 2:

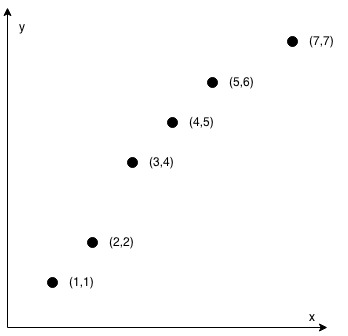
Input:
coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
Output:
 false

Solution

Method 1 – Cross Product Consistency

Intuition

All points are in a straight line if the slope between every pair of consecutive points is the same. To avoid division and floating point issues, we use the cross product: for points (x0, y0), (x1, y1), (xi, yi), the vectors (x1-x0, y1-y0) and (xi-x0, yi-y0) should be collinear, i.e., (x1-x0)(yi-y0) == (y1-y0)(xi-x0).

Approach

  1. Compute the direction vector (dx, dy) from the first two points.
  2. For each subsequent point, check if the cross product with the direction vector is zero.
  3. If all checks pass, the points are collinear.

Code

C++
class Solution {
public:
    bool checkStraightLine(vector<vector<int>>& c) {
        int dx = c[1][0] - c[0][0], dy = c[1][1] - c[0][1];
        for (int i = 2; i < c.size(); ++i) {
            if (dx * (c[i][1] - c[0][1]) != dy * (c[i][0] - c[0][0]))
                return false;
        }
        return true;
    }
};
Go
func checkStraightLine(c [][]int) bool {
    dx, dy := c[1][0]-c[0][0], c[1][1]-c[0][1]
    for i := 2; i < len(c); i++ {
        if dx*(c[i][1]-c[0][1]) != dy*(c[i][0]-c[0][0]) {
            return false
        }
    }
    return true
}
Java
class Solution {
    public boolean checkStraightLine(int[][] c) {
        int dx = c[1][0] - c[0][0], dy = c[1][1] - c[0][1];
        for (int i = 2; i < c.length; i++) {
            if (dx * (c[i][1] - c[0][1]) != dy * (c[i][0] - c[0][0]))
                return false;
        }
        return true;
    }
}
Kotlin
class Solution {
    fun checkStraightLine(c: Array<IntArray>): Boolean {
        val dx = c[1][0] - c[0][0]
        val dy = c[1][1] - c[0][1]
        for (i in 2 until c.size) {
            if (dx * (c[i][1] - c[0][1]) != dy * (c[i][0] - c[0][0]))
                return false
        }
        return true
    }
}
Python
class Solution:
    def checkStraightLine(self, c: list[list[int]]) -> bool:
        dx, dy = c[1][0] - c[0][0], c[1][1] - c[0][1]
        for i in range(2, len(c)):
            if dx * (c[i][1] - c[0][1]) != dy * (c[i][0] - c[0][0]):
                return False
        return True
Rust
impl Solution {
    pub fn check_straight_line(c: Vec<Vec<i32>>) -> bool {
        let dx = c[1][0] - c[0][0];
        let dy = c[1][1] - c[0][1];
        for i in 2..c.len() {
            if dx * (c[i][1] - c[0][1]) != dy * (c[i][0] - c[0][0]) {
                return false;
            }
        }
        true
    }
}
TypeScript
class Solution {
    checkStraightLine(c: number[][]): boolean {
        const dx = c[1][0] - c[0][0], dy = c[1][1] - c[0][1];
        for (let i = 2; i < c.length; i++) {
            if (dx * (c[i][1] - c[0][1]) !== dy * (c[i][0] - c[0][0]))
                return false;
        }
        return true;
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of points.
  • 🧺 Space complexity: O(1), only constant extra space is used.

Comments