Check if Matrix Is X-Matrix

Problem

A square matrix is said to be an X-Matrix if both of the following conditions hold:

1. All the elements in the diagonals of the matrix are non-zero.
2. All other elements are 0.

Given a 2D integer array grid of size n x n representing a square matrix, return true ifgrid is an X-Matrix. Otherwise, return false.

Examples

Example 1

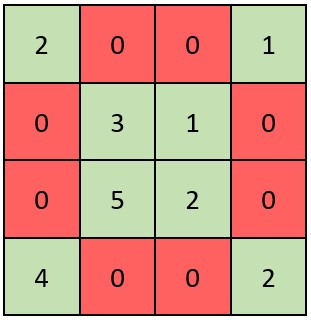
Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
Output: true
Explanation: Refer to the diagram above. 
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.

Example 2

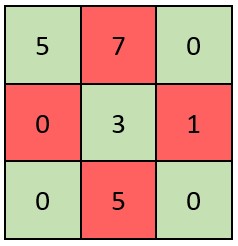
Input: grid = [[5,7,0],[0,3,1],[0,5,0]]
Output: false
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.

Constraints

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 0 <= grid[i][j] <= 10^5

Solution

Method 1 – Direct Diagonal and Off-Diagonal Check

Intuition

For a matrix to be an X-Matrix, all diagonal elements (main and anti-diagonal) must be non-zero, and all other elements must be zero. We can check each cell and verify these conditions directly.

Approach

1. Let n be the size of the matrix.
2. For each cell (i, j):
   • If i == j or i + j == n - 1 (diagonal positions): check grid[i][j] != 0.
   • Else (off-diagonal): check grid[i][j] == 0.
3. If all checks pass, return true; otherwise, return false.

Code

C++

class Solution {
public:
    bool checkXMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    if (grid[i][j] == 0) return false;
                } else {
                    if (grid[i][j] != 0) return false;
                }
            }
        }
        return true;
    }
};

Go

func checkXMatrix(grid [][]int) bool {
    n := len(grid)
    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            if i == j || i+j == n-1 {
                if grid[i][j] == 0 {
                    return false
                }
            } else {
                if grid[i][j] != 0 {
                    return false
                }
            }
        }
    }
    return true
}

Java

class Solution {
    public boolean checkXMatrix(int[][] grid) {
        int n = grid.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    if (grid[i][j] == 0) return false;
                } else {
                    if (grid[i][j] != 0) return false;
                }
            }
        }
        return true;
    }
}

Kotlin

class Solution {
    fun checkXMatrix(grid: Array<IntArray>): Boolean {
        val n = grid.size
        for (i in 0 until n) {
            for (j in 0 until n) {
                if (i == j || i + j == n - 1) {
                    if (grid[i][j] == 0) return false
                } else {
                    if (grid[i][j] != 0) return false
                }
            }
        }
        return true
    }
}

Python

class Solution:
    def checkXMatrix(self, grid: list[list[int]]) -> bool:
        n = len(grid)
        for i in range(n):
            for j in range(n):
                if i == j or i + j == n - 1:
                    if grid[i][j] == 0:
                        return False
                else:
                    if grid[i][j] != 0:
                        return False
        return True

Rust

impl Solution {
    pub fn check_x_matrix(grid: Vec<Vec<i32>>) -> bool {
        let n = grid.len();
        for i in 0..n {
            for j in 0..n {
                if i == j || i + j == n - 1 {
                    if grid[i][j] == 0 {
                        return false;
                    }
                } else {
                    if grid[i][j] != 0 {
                        return false;
                    }
                }
            }
        }
        true
    }
}

Complexity

• ⏰ Time complexity: O(n^2), where n is the size of the matrix.
• 🧺 Space complexity: O(1)