Check if the Rectangle Corner Is Reachable
HardUpdated: Jul 7, 2025
Practice on:
Problem
You are given two positive integers xCorner and yCorner, and a 2D array circles, where circles[i] = [xi, yi, ri] denotes a circle with center at (xi, yi) and radius ri.
There is a rectangle in the coordinate plane with its bottom left corner at the origin and top right corner at the coordinate (xCorner, yCorner). You need to check whether there is a path from the bottom left corner to the top right corner such that the entire path lies inside the rectangle, does not touch or lie inside any circle, and touches the rectangle only at the two corners.
Return true if such a path exists, and false otherwise.
Examples
Example 1
Input: xCorner = 3, yCorner = 4, circles = [[2,1,1]]
Output: true
Explanation:
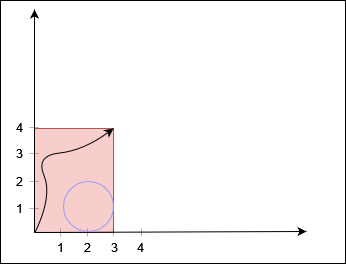The black curve shows a possible path between (0, 0) and (3, 4).
Example 2
Input: xCorner = 3, yCorner = 3, circles = [[1,1,2]]
Output: false
Explanation:
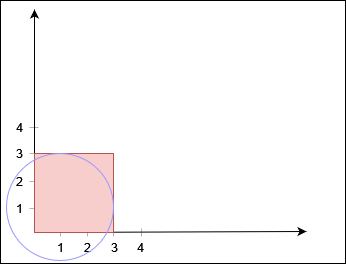No path exists from (0, 0) to (3, 3).
Example 3
Input: xCorner = 3, yCorner = 3, circles = [[2,1,1],[1,2,1]]
Output: false
Explanation:
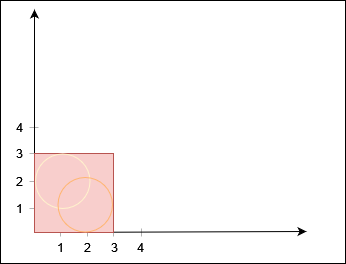No path exists from (0, 0) to (3, 3).
Example 4
Input: xCorner = 4, yCorner = 4, circles = [[5,5,1]]
Output: true
Explanation:
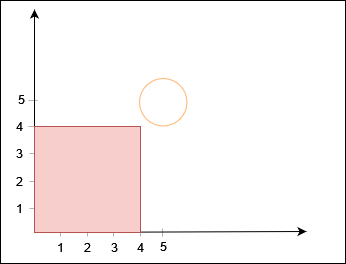
Constraints
3 <= xCorner, yCorner <= 10^91 <= circles.length <= 1000circles[i].length == 31 <= xi, yi, ri <= 10^9
Solution
Method 1 – BFS/DFS with Grid Marking
Intuition
We need to find a path from (0,0) to (xCorner, yCorner) inside the rectangle, avoiding all circles. The problem reduces to a grid-based pathfinding problem with forbidden cells (those inside or on any circle). BFS or DFS can be used to explore the grid.
Reasoning
By marking all points that are inside or on any circle as blocked, we can use BFS or DFS to check if there is a path from the bottom-left to the top-right corner. Since the rectangle is small (max 100x100), this approach is efficient.
Approach
- Create a grid of size (xCorner+1) x (yCorner+1), initialized as unblocked.
- For each cell (x, y), check if it is inside or on any circle. If so, mark it as blocked.
- Use BFS or DFS to search for a path from (0,0) to (xCorner, yCorner), only moving to unblocked cells.
- Return true if a path exists, otherwise false.
Edge cases:
- The start or end cell is blocked.
- No circles: always possible.
Code
C++
class Solution {
public:
bool isReachable(int xCorner, int yCorner, vector<vector<int>>& circles) {
int n = xCorner, m = yCorner;
vector<vector<bool>> blocked(n+1, vector<bool>(m+1, false));
for (auto& c : circles) {
int cx = c[0], cy = c[1], r = c[2];
for (int x = 0; x <= n; ++x) {
for (int y = 0; y <= m; ++y) {
int dx = x - cx, dy = y - cy;
if (dx*dx + dy*dy <= r*r) blocked[x][y] = true;
}
}
}
if (blocked[0][0] || blocked[n][m]) return false;
queue<pair<int,int>> q;
q.push({0,0});
blocked[0][0] = true;
int dirs[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
while (!q.empty()) {
auto [x, y] = q.front(); q.pop();
if (x == n && y == m) return true;
for (auto& d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx >= 0 && nx <= n && ny >= 0 && ny <= m && !blocked[nx][ny]) {
blocked[nx][ny] = true;
q.push({nx, ny});
}
}
}
return false;
}
};
Go
func isReachable(xCorner, yCorner int, circles [][]int) bool {
n, m := xCorner, yCorner
blocked := make([][]bool, n+1)
for i := range blocked {
blocked[i] = make([]bool, m+1)
}
for _, c := range circles {
cx, cy, r := c[0], c[1], c[2]
for x := 0; x <= n; x++ {
for y := 0; y <= m; y++ {
dx, dy := x-cx, y-cy
if dx*dx+dy*dy <= r*r {
blocked[x][y] = true
}
}
}
}
if blocked[0][0] || blocked[n][m] {
return false
}
dirs := [][2]int{{1,0},{-1,0},{0,1},{0,-1}}
q := [][2]int{{0,0}}
blocked[0][0] = true
for len(q) > 0 {
x, y := q[0][0], q[0][1]
q = q[1:]
if x == n && y == m {
return true
}
for _, d := range dirs {
nx, ny := x+d[0], y+d[1]
if nx >= 0 && nx <= n && ny >= 0 && ny <= m && !blocked[nx][ny] {
blocked[nx][ny] = true
q = append(q, [2]int{nx, ny})
}
}
}
return false
}
Java
class Solution {
public boolean isReachable(int xCorner, int yCorner, int[][] circles) {
int n = xCorner, m = yCorner;
boolean[][] blocked = new boolean[n+1][m+1];
for (int[] c : circles) {
int cx = c[0], cy = c[1], r = c[2];
for (int x = 0; x <= n; x++) {
for (int y = 0; y <= m; y++) {
int dx = x - cx, dy = y - cy;
if (dx*dx + dy*dy <= r*r) blocked[x][y] = true;
}
}
}
if (blocked[0][0] || blocked[n][m]) return false;
Queue<int[]> q = new LinkedList<>();
q.add(new int[]{0,0});
blocked[0][0] = true;
int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};
while (!q.isEmpty()) {
int[] cur = q.poll();
int x = cur[0], y = cur[1];
if (x == n && y == m) return true;
for (int[] d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx >= 0 && nx <= n && ny >= 0 && ny <= m && !blocked[nx][ny]) {
blocked[nx][ny] = true;
q.add(new int[]{nx, ny});
}
}
}
return false;
}
}
Kotlin
class Solution {
fun isReachable(xCorner: Int, yCorner: Int, circles: Array<IntArray>): Boolean {
val n = xCorner; val m = yCorner
val blocked = Array(n+1) { BooleanArray(m+1) }
for (c in circles) {
val cx = c[0]; val cy = c[1]; val r = c[2]
for (x in 0..n) for (y in 0..m) {
val dx = x - cx; val dy = y - cy
if (dx*dx + dy*dy <= r*r) blocked[x][y] = true
}
}
if (blocked[0][0] || blocked[n][m]) return false
val dirs = arrayOf(intArrayOf(1,0), intArrayOf(-1,0), intArrayOf(0,1), intArrayOf(0,-1))
val q = ArrayDeque<Pair<Int,Int>>()
q.add(0 to 0)
blocked[0][0] = true
while (q.isNotEmpty()) {
val (x, y) = q.removeFirst()
if (x == n && y == m) return true
for (d in dirs) {
val nx = x + d[0]; val ny = y + d[1]
if (nx in 0..n && ny in 0..m && !blocked[nx][ny]) {
blocked[nx][ny] = true
q.add(nx to ny)
}
}
}
return false
}
}
Python
class Solution:
def is_reachable(self, xCorner: int, yCorner: int, circles: list[list[int]]) -> bool:
n, m = xCorner, yCorner
blocked = [[False]*(m+1) for _ in range(n+1)]
for cx, cy, r in circles:
for x in range(n+1):
for y in range(m+1):
if (x-cx)**2 + (y-cy)**2 <= r*r:
blocked[x][y] = True
if blocked[0][0] or blocked[n][m]:
return False
from collections import deque
q = deque([(0,0)])
blocked[0][0] = True
dirs = [(1,0),(-1,0),(0,1),(0,-1)]
while q:
x, y = q.popleft()
if x == n and y == m:
return True
for dx, dy in dirs:
nx, ny = x+dx, y+dy
if 0 <= nx <= n and 0 <= ny <= m and not blocked[nx][ny]:
blocked[nx][ny] = True
q.append((nx, ny))
return False
Rust
impl Solution {
pub fn is_reachable(x_corner: i32, y_corner: i32, circles: Vec<Vec<i32>>) -> bool {
let n = x_corner as usize;
let m = y_corner as usize;
let mut blocked = vec![vec![false; m+1]; n+1];
for c in &circles {
let (cx, cy, r) = (c[0], c[1], c[2]);
for x in 0..=n {
for y in 0..=m {
let dx = x as i32 - cx;
let dy = y as i32 - cy;
if dx*dx + dy*dy <= r*r {
blocked[x][y] = true;
}
}
}
}
if blocked[0][0] || blocked[n][m] {
return false;
}
let dirs = [(1,0),(-1,0),(0,1),(0,-1)];
let mut q = std::collections::VecDeque::new();
q.push_back((0,0));
blocked[0][0] = true;
while let Some((x, y)) = q.pop_front() {
if x == n && y == m {
return true;
}
for (dx, dy) in dirs.iter() {
let nx = x as i32 + dx;
let ny = y as i32 + dy;
if nx >= 0 && nx <= n as i32 && ny >= 0 && ny <= m as i32 && !blocked[nx as usize][ny as usize] {
blocked[nx as usize][ny as usize] = true;
q.push_back((nx as usize, ny as usize));
}
}
}
false
}
}
Complexity
- ⏰ Time complexity:
O((n*m)*k), wherenandmare the rectangle dimensions andkis the number of circles, as we check each cell for each circle and perform BFS/DFS. - 🧺 Space complexity:
O(n*m), as we store the blocked grid and BFS/DFS queue.