Problem

You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1).

Return true if there is a path from(0, 0)to(m - 1, n - 1)_that visits anequal number of _0 _’ s and _1 ’ s. Otherwise return false.

Examples

Example 1: 

1
2
3

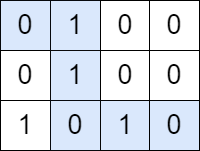
Input: grid = [[0,1,0,0],[0,1,0,0],[1,0,1,0]]
Output: true
Explanation: The path colored in blue in the above diagram is a valid path because we have 3 cells with a value of 1 and 3 with a value of 0. Since there is a valid path, we return true.

Example 2: 

1
2
3

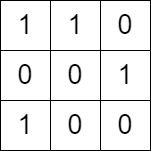
Input: grid = [[1,1,0],[0,0,1],[1,0,0]]
Output: false
Explanation: There is no path in this grid with an equal number of 0's and 1's.

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 100
  • grid[i][j] is either 0 or 1.

Solution

Method 1 – Dynamic Programming with Balance Tracking

Intuition

We need to find a path from the top-left to the bottom-right of the grid such that the number of 0’s and 1’s is equal. Since we can only move right or down, and the path length is fixed, we can use dynamic programming to track the possible balances (difference between 1’s and 0’s) at each cell.

Reasoning

At each cell, the only information that matters is the current balance (number of 1’s minus number of 0’s) and the position. We can use a set to track all possible balances at each cell, propagating from the top-left to the bottom-right. If a balance of 0 is possible at the end, then a valid path exists.

Approach

  1. Let m and n be the grid dimensions. The path length is m + n - 1.
  2. If the path length is odd, return false (cannot split evenly between 0’s and 1’s).
  3. Use a DP table where dp[i][j] is a set of possible balances at cell (i, j).
  4. Initialize dp[0][0] with the balance at the starting cell.
  5. For each cell, propagate possible balances from the top and left neighbors, updating the balance according to the current cell’s value.
  6. At the end, check if a balance of 0 is possible at the bottom-right cell.

Edge cases:

  • Path length is odd: impossible.
  • All 0’s or all 1’s: impossible.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    bool isThereAPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        if ((m + n - 1) % 2) return false;
        vector<vector<unordered_set<int>>> dp(m, vector<unordered_set<int>>(n));
        dp[0][0].insert(grid[0][0] == 1 ? 1 : -1);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int d : {0, 1}) {
                    int ni = i - d, nj = j - (1 - d);
                    if (ni >= 0 && nj >= 0) {
                        for (int bal : dp[ni][nj]) {
                            int nb = bal + (grid[i][j] == 1 ? 1 : -1);
                            dp[i][j].insert(nb);
                        }
                    }
                }
            }
        }
        return dp[m-1][n-1].count(0);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution:
    def is_there_a_path(self, grid: list[list[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        if (m + n - 1) % 2:
            return False
        from collections import defaultdict
        dp = [[set() for _ in range(n)] for _ in range(m)]
        dp[0][0].add(1 if grid[0][0] == 1 else -1)
        for i in range(m):
            for j in range(n):
                for ni, nj in ((i-1, j), (i, j-1)):
                    if 0 <= ni < m and 0 <= nj < n:
                        for bal in dp[ni][nj]:
                            nb = bal + (1 if grid[i][j] == 1 else -1)
                            dp[i][j].add(nb)
        return 0 in dp[m-1][n-1]

Complexity

  • ⏰ Time complexity: O(m * n * k), where k is the number of possible balances (at most m+n), as we track all possible balances at each cell.
  • 🧺 Space complexity: O(m * n * k), as we store possible balances for each cell.