Problem

You are given an m x n grid. Each cell of grid represents a street. The street of grid[i][j] can be:

  • 1 which means a street connecting the left cell and the right cell.
  • 2 which means a street connecting the upper cell and the lower cell.
  • 3 which means a street connecting the left cell and the lower cell.
  • 4 which means a street connecting the right cell and the lower cell.
  • 5 which means a street connecting the left cell and the upper cell.
  • 6 which means a street connecting the right cell and the upper cell.

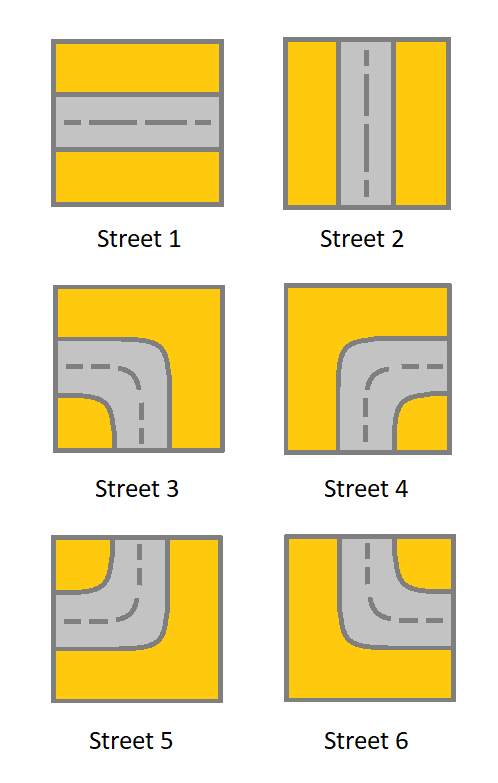
You will initially start at the street of the upper-left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid orfalse otherwise.

Examples

Example 1

1
2
3

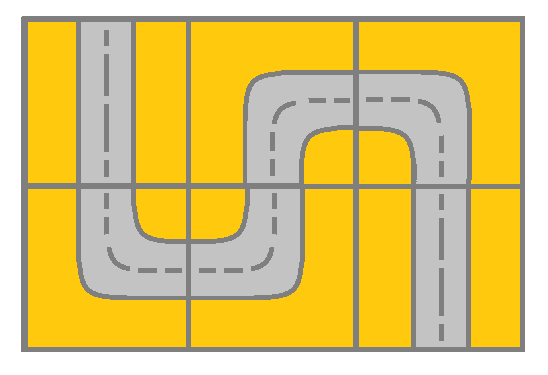
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2

1
2
3

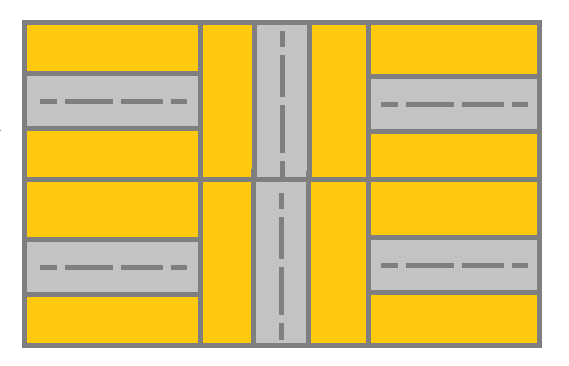
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3

1
2
3

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Constraints

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • 1 <= grid[i][j] <= 6

Solution

Method 1 – BFS/DFS with Direction Mapping

Intuition

Each cell type allows movement in certain directions, and only if the adjacent cell allows entry from that direction. We can use BFS or DFS to traverse the grid, only moving to valid neighboring cells according to the street types.

Reasoning

For each cell, we check all possible directions it can move to, and for each move, verify that the next cell allows entry from the opposite direction. If we can reach the bottom-right cell, a valid path exists. This works because the grid is small and each move is strictly determined by the street types.

Approach

  1. Define the allowed directions for each street type and the required entry direction for each type.
  2. Use BFS or DFS starting from (0,0), marking visited cells.
  3. For each move, check if the next cell is within bounds, not visited, and allows entry from the current direction.
  4. If we reach (m-1, n-1), return true. If BFS/DFS ends, return false.

Edge cases:

  • Single cell grid: always true.
  • No valid moves from the start: false.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
public:
    bool hasValidPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<bool>> vis(m, vector<bool>(n, false));
        vector<vector<vector<int>>> dirs = {
            {},
            {{0,-1},{0,1}},    // 1: left, right
            {{-1,0},{1,0}},    // 2: up, down
            {{0,-1},{1,0}},    // 3: left, down
            {{0,1},{1,0}},     // 4: right, down
            {{0,-1},{-1,0}},   // 5: left, up
            {{0,1},{-1,0}}     // 6: right, up
        };
        queue<pair<int,int>> q;
        q.push({0,0});
        vis[0][0] = true;
        while (!q.empty()) {
            auto [x, y] = q.front(); q.pop();
            if (x == m-1 && y == n-1) return true;
            for (auto& d : dirs[grid[x][y]]) {
                int nx = x + d[0], ny = y + d[1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n || vis[nx][ny]) continue;
                for (auto& back : dirs[grid[nx][ny]]) {
                    if (nx + back[0] == x && ny + back[1] == y) {
                        vis[nx][ny] = true;
                        q.push({nx, ny});
                        break;
                    }
                }
            }
        }
        return false;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution:
    def has_valid_path(self, grid: list[list[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        dirs = {
            1: [(0,-1),(0,1)],
            2: [(-1,0),(1,0)],
            3: [(0,-1),(1,0)],
            4: [(0,1),(1,0)],
            5: [(0,-1),(-1,0)],
            6: [(0,1),(-1,0)]
        }
        vis = [[False]*n for _ in range(m)]
        from collections import deque
        q = deque([(0,0)])
        vis[0][0] = True
        while q:
            x, y = q.popleft()
            if x == m-1 and y == n-1:
                return True
            for dx, dy in dirs[grid[x][y]]:
                nx, ny = x+dx, y+dy
                if 0 <= nx < m and 0 <= ny < n and not vis[nx][ny]:
                    for bdx, bdy in dirs[grid[nx][ny]]:
                        if nx+bdx == x and ny+bdy == y:
                            vis[nx][ny] = True
                            q.append((nx, ny))
                            break
        return False
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
    public boolean hasValidPath(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        boolean[][] vis = new boolean[m][n];
        int[][][] dirs = {
            {},
            {{0,-1},{0,1}},    // 1: left, right
            {{-1,0},{1,0}},    // 2: up, down
            {{0,-1},{1,0}},    // 3: left, down
            {{0,1},{1,0}},     // 4: right, down
            {{0,-1},{-1,0}},   // 5: left, up
            {{0,1},{-1,0}}     // 6: right, up
        };
        Queue<int[]> q = new LinkedList<>();
        q.add(new int[]{0,0});
        vis[0][0] = true;
        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int x = cur[0], y = cur[1];
            if (x == m-1 && y == n-1) return true;
            for (int[] d : dirs[grid[x][y]]) {
                int nx = x + d[0], ny = y + d[1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n || vis[nx][ny]) continue;
                for (int[] back : dirs[grid[nx][ny]]) {
                    if (nx + back[0] == x && ny + back[1] == y) {
                        vis[nx][ny] = true;
                        q.add(new int[]{nx, ny});
                        break;
                    }
                }
            }
        }
        return false;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
    fun hasValidPath(grid: Array<IntArray>): Boolean {
        val m = grid.size; val n = grid[0].size
        val dirs = arrayOf(
            arrayOf(),
            arrayOf(intArrayOf(0,-1), intArrayOf(0,1)),
            arrayOf(intArrayOf(-1,0), intArrayOf(1,0)),
            arrayOf(intArrayOf(0,-1), intArrayOf(1,0)),
            arrayOf(intArrayOf(0,1), intArrayOf(1,0)),
            arrayOf(intArrayOf(0,-1), intArrayOf(-1,0)),
            arrayOf(intArrayOf(0,1), intArrayOf(-1,0))
        )
        val vis = Array(m) { BooleanArray(n) }
        val q = ArrayDeque<Pair<Int,Int>>()
        q.add(0 to 0)
        vis[0][0] = true
        while (q.isNotEmpty()) {
            val (x, y) = q.removeFirst()
            if (x == m-1 && y == n-1) return true
            for (d in dirs[grid[x][y]]) {
                val nx = x + d[0]; val ny = y + d[1]
                if (nx !in 0 until m || ny !in 0 until n || vis[nx][ny]) continue
                for (back in dirs[grid[nx][ny]]) {
                    if (nx + back[0] == x && ny + back[1] == y) {
                        vis[nx][ny] = true
                        q.add(nx to ny)
                        break
                    }
                }
            }
        }
        return false
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

impl Solution {
    pub fn has_valid_path(grid: Vec<Vec<i32>>) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        let dirs = vec![
            vec![],
            vec![(0,-1),(0,1)],
            vec![(-1,0),(1,0)],
            vec![(0,-1),(1,0)],
            vec![(0,1),(1,0)],
            vec![(0,-1),(-1,0)],
            vec![(0,1),(-1,0)]
        ];
        let mut vis = vec![vec![false; n]; m];
        let mut q = std::collections::VecDeque::new();
        q.push_back((0,0));
        vis[0][0] = true;
        while let Some((x, y)) = q.pop_front() {
            if x == m-1 && y == n-1 {
                return true;
            }
            for &(dx, dy) in &dirs[grid[x][y] as usize] {
                let nx = x as i32 + dx;
                let ny = y as i32 + dy;
                if nx < 0 || nx >= m as i32 || ny < 0 || ny >= n as i32 || vis[nx as usize][ny as usize] {
                    continue;
                }
                for &(bdx, bdy) in &dirs[grid[nx as usize][ny as usize] as usize] {
                    if nx + bdx == x as i32 && ny + bdy == y as i32 {
                        vis[nx as usize][ny as usize] = true;
                        q.push_back((nx as usize, ny as usize));
                        break;
                    }
                }
            }
        }
        false
    }
}

Complexity

  • ⏰ Time complexity: O(m * n), as each cell is visited at most once and each move is constant time.
  • 🧺 Space complexity: O(m * n), as we store the visited grid and BFS/DFS queue.