Problem

A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (variables), and internal nodes (nodes with two children) correspond to the operators. In this problem, we only consider the '+' operator (i.e. addition).

You are given the roots of two binary expression trees, root1 and root2. Return true if the two binary expression trees are equivalent. Otherwise, return false.

Two binary expression trees are equivalent if they evaluate to the same value regardless of what the variables are set to.

Examples

Example 1:

1
2

Input: root1 = [x], root2 = [x]
Output: true

Example 2: 

1
2
3

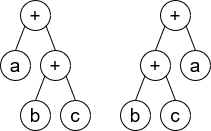
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
Output: true
**Explanation****:** a + (b + c) == (b + c) + a

Example 3: 

1
2
3

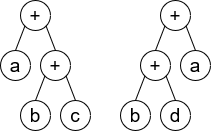
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
Output: false
**Explanation****:** a + (b + c) != (b + d) + a

Constraints:

  • The number of nodes in both trees are equal, odd and, in the range [1, 4999].
  • Node.val is '+' or a lower-case English letter.
  • It’s guaranteed that the tree given is a valid binary expression tree.

Follow up: What will you change in your solution if the tree also supports the '-' operator (i.e. subtraction)?

Solution

Method 1 – Variable Counting via DFS

Intuition

Since only the ‘+’ operator is used and addition is both commutative and associative, the order and grouping of variables do not matter. Thus, two trees are equivalent if they contain the same multiset of variables.

Reasoning

By traversing each tree and counting the occurrences of each variable, we can compare the two trees. If the variable counts match, the trees are equivalent for any variable assignment.

Approach

  1. Define a DFS function to traverse the tree and count variables in a hash map.
  2. For each tree, perform DFS and collect variable counts.
  3. Compare the two hash maps for equality.
  4. Return true if they match, otherwise false.

Edge cases:

  • Both trees are a single variable.
  • Trees with repeated variables.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    void dfs(TreeNode* node, unordered_map<string, int>& cnt) {
        if (!node->left && !node->right) {
            cnt[node->val]++;
            return;
        }
        dfs(node->left, cnt);
        dfs(node->right, cnt);
    }
    bool checkEquivalence(TreeNode* root1, TreeNode* root2) {
        unordered_map<string, int> cnt1, cnt2;
        dfs(root1, cnt1);
        dfs(root2, cnt2);
        return cnt1 == cnt2;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

func checkEquivalence(root1, root2 *Node) bool {
    var dfs func(*Node, map[string]int)
    dfs = func(node *Node, cnt map[string]int) {
        if node.Left == nil && node.Right == nil {
            cnt[node.Val]++
            return
        }
        dfs(node.Left, cnt)
        dfs(node.Right, cnt)
    }
    cnt1, cnt2 := map[string]int{}, map[string]int{}
    dfs(root1, cnt1)
    dfs(root2, cnt2)
    if len(cnt1) != len(cnt2) {
        return false
    }
    for k, v := range cnt1 {
        if cnt2[k] != v {
            return false
        }
    }
    return true
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    void dfs(Node node, Map<String, Integer> cnt) {
        if (node.left == null && node.right == null) {
            cnt.put(node.val, cnt.getOrDefault(node.val, 0) + 1);
            return;
        }
        dfs(node.left, cnt);
        dfs(node.right, cnt);
    }
    public boolean checkEquivalence(Node root1, Node root2) {
        Map<String, Integer> cnt1 = new HashMap<>(), cnt2 = new HashMap<>();
        dfs(root1, cnt1);
        dfs(root2, cnt2);
        return cnt1.equals(cnt2);
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
    fun checkEquivalence(root1: Node?, root2: Node?): Boolean {
        fun dfs(node: Node?, cnt: MutableMap<String, Int>) {
            if (node?.left == null && node?.right == null) {
                cnt[node!!.val] = cnt.getOrDefault(node.val, 0) + 1
                return
            }
            dfs(node?.left, cnt)
            dfs(node?.right, cnt)
        }
        val cnt1 = mutableMapOf<String, Int>()
        val cnt2 = mutableMapOf<String, Int>()
        dfs(root1, cnt1)
        dfs(root2, cnt2)
        return cnt1 == cnt2
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution:
    def check_equivalence(self, root1: 'Node', root2: 'Node') -> bool:
        def dfs(node: 'Node', cnt: dict[str, int]):
            if not node.left and not node.right:
                cnt[node.val] = cnt.get(node.val, 0) + 1
                return
            dfs(node.left, cnt)
            dfs(node.right, cnt)
        cnt1, cnt2 = {}, {}
        dfs(root1, cnt1)
        dfs(root2, cnt2)
        return cnt1 == cnt2
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

impl Solution {
    pub fn check_equivalence(root1: Option<Rc<RefCell<Node>>>, root2: Option<Rc<RefCell<Node>>>) -> bool {
        use std::collections::HashMap;
        fn dfs(node: Option<Rc<RefCell<Node>>>, cnt: &mut HashMap<String, i32>) {
            if let Some(n) = node {
                let n = n.borrow();
                if n.left.is_none() && n.right.is_none() {
                    *cnt.entry(n.val.clone()).or_insert(0) += 1;
                    return;
                }
                dfs(n.left.clone(), cnt);
                dfs(n.right.clone(), cnt);
            }
        }
        let mut cnt1 = HashMap::new();
        let mut cnt2 = HashMap::new();
        dfs(root1, &mut cnt1);
        dfs(root2, &mut cnt2);
        cnt1 == cnt2
    }
}

Complexity

  • ⏰ Time complexity: O(n), as each node is visited once and variable counting is constant time per node.
  • 🧺 Space complexity: O(n), as we store the variable counts for each tree.