Problem

There is a knight on an n x n chessboard. In a valid configuration, the knight starts at the top-left cell of the board and visits every cell on the board exactly once.

You are given an n x n integer matrix grid consisting of distinct integers from the range [0, n * n - 1] where grid[row][col] indicates that the cell (row, col) is the grid[row][col]th cell that the knight visited. The moves are 0-indexed.

Return true if grid represents a valid configuration of the knight ’s movements or false otherwise.

Note that a valid knight move consists of moving two squares vertically and one square horizontally, or two squares horizontally and one square vertically. The figure below illustrates all the possible eight moves of a knight from some cell.

Examples

Example 1

1
2
3

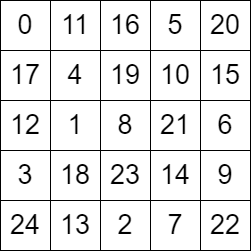
Input: grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]
Output: true
Explanation: The above diagram represents the grid. It can be shown that it is a valid configuration.

Example 2

1
2
3

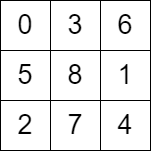
Input: grid = [[0,3,6],[5,8,1],[2,7,4]]
Output: false
Explanation: The above diagram represents the grid. The 8th move of the knight is not valid considering its position after the 7th move.

Constraints

  • n == grid.length == grid[i].length
  • 3 <= n <= 7
  • 0 <= grid[row][col] < n * n
  • All integers in grid are unique.

Solution

Method 1 – Sequential Move Validation

Intuition

A valid knight tour must start at (0,0) and each move from step k to k+1 must be a valid knight move. We can map each move number to its position and check all consecutive moves.

Reasoning

By storing the position of each move, we can check if each consecutive move is a valid knight move (i.e., the difference in coordinates is (2,1) or (1,2) in any direction). If all moves are valid, the configuration is valid.

Approach

  1. Create a mapping from move number to (row, col) position.
  2. Check that move 0 is at (0,0).
  3. For each move from 0 to n*n-2:
    • Get the current and next positions.
    • Check if the move is a valid knight move (abs(dx), abs(dy)) in [(1,2),(2,1)].
    • If any move is invalid, return false.
  4. If all moves are valid, return true.

Edge cases:

  • n < 3: not possible by constraints.
  • Any move out of knight’s reach: invalid.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    bool checkValidGrid(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<pair<int,int>> pos(n*n);
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                pos[grid[i][j]] = {i, j};
        if (pos[0] != make_pair(0,0)) return false;
        for (int k = 0; k < n*n-1; ++k) {
            int dx = abs(pos[k+1].first - pos[k].first);
            int dy = abs(pos[k+1].second - pos[k].second);
            if (!((dx == 1 && dy == 2) || (dx == 2 && dy == 1))) return false;
        }
        return true;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

func checkValidGrid(grid [][]int) bool {
    n := len(grid)
    pos := make([][2]int, n*n)
    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            pos[grid[i][j]] = [2]int{i, j}
        }
    }
    if pos[0] != [2]int{0, 0} {
        return false
    }
    for k := 0; k < n*n-1; k++ {
        dx := abs(pos[k+1][0] - pos[k][0])
        dy := abs(pos[k+1][1] - pos[k][1])
        if !((dx == 1 && dy == 2) || (dx == 2 && dy == 1)) {
            return false
        }
    }
    return true
}
func abs(x int) int { if x < 0 { return -x }; return x }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public boolean checkValidGrid(int[][] grid) {
        int n = grid.length;
        int[][] pos = new int[n*n][2];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                pos[grid[i][j]] = new int[]{i, j};
        if (pos[0][0] != 0 || pos[0][1] != 0) return false;
        for (int k = 0; k < n*n-1; k++) {
            int dx = Math.abs(pos[k+1][0] - pos[k][0]);
            int dy = Math.abs(pos[k+1][1] - pos[k][1]);
            if (!((dx == 1 && dy == 2) || (dx == 2 && dy == 1))) return false;
        }
        return true;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    fun checkValidGrid(grid: Array<IntArray>): Boolean {
        val n = grid.size
        val pos = Array(n*n) { IntArray(2) }
        for (i in 0 until n) for (j in 0 until n) pos[grid[i][j]] = intArrayOf(i, j)
        if (pos[0][0] != 0 || pos[0][1] != 0) return false
        for (k in 0 until n*n-1) {
            val dx = Math.abs(pos[k+1][0] - pos[k][0])
            val dy = Math.abs(pos[k+1][1] - pos[k][1])
            if (!((dx == 1 && dy == 2) || (dx == 2 && dy == 1))) return false
        }
        return true
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution:
    def check_valid_grid(self, grid: list[list[int]]) -> bool:
        n = len(grid)
        pos = [(-1, -1)] * (n * n)
        for i in range(n):
            for j in range(n):
                pos[grid[i][j]] = (i, j)
        if pos[0] != (0, 0):
            return False
        for k in range(n * n - 1):
            dx = abs(pos[k+1][0] - pos[k][0])
            dy = abs(pos[k+1][1] - pos[k][1])
            if not ((dx == 1 and dy == 2) or (dx == 2 and dy == 1)):
                return False
        return True
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

impl Solution {
    pub fn check_valid_grid(grid: Vec<Vec<i32>>) -> bool {
        let n = grid.len();
        let mut pos = vec![(0, 0); n * n];
        for i in 0..n {
            for j in 0..n {
                pos[grid[i][j] as usize] = (i as i32, j as i32);
            }
        }
        if pos[0] != (0, 0) {
            return false;
        }
        for k in 0..n * n - 1 {
            let dx = (pos[k + 1].0 - pos[k].0).abs();
            let dy = (pos[k + 1].1 - pos[k].1).abs();
            if !((dx == 1 && dy == 2) || (dx == 2 && dy == 1)) {
                return false;
            }
        }
        true
    }
}

Complexity

  • ⏰ Time complexity: O(n^2), as we scan the grid and check all moves.
  • 🧺 Space complexity: O(n^2), as we store the position of each move.