Cinema Seat Allocation

Problem

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.

Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.

Examples

Example 1

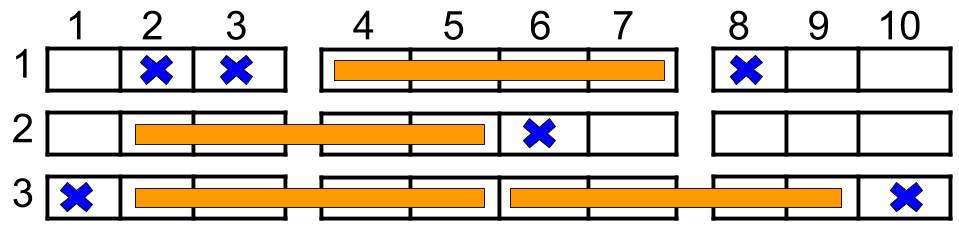
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.

Example 2

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

Constraints

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

Solution

Method 1 – Greedy with Bitmasking

Intuition

The main idea is to use bitmasking to efficiently represent reserved seats in each row. For each row with reservations, we check which four-seat blocks (left, middle, right) are available. Rows without any reservations can always fit two groups.

Approach

1. Use a map to record reserved seats for each row as a bitmask.
2. For each row with reservations:
   • Check if the left block (seats 2-5), middle block (seats 4-7), or right block (seats 6-9) are all free.
   • Count the number of groups that can be placed in that row (max 2).
3. For rows without any reservations, add 2 groups per row.
4. Sum the total number of groups.

Code

C++

class Solution {
public:
    int maxNumberOfFamilies(int n, vector<vector<int>>& reservedSeats) {
        unordered_map<int, int> row;
        for (auto& r : reservedSeats)
            row[r[0]] |= 1 << (r[1] - 1);
        int ans = (n - row.size()) * 2;
        for (auto& [_, mask] : row) {
            int cnt = 0;
            if ((mask & 0b0000011110) == 0) cnt++;
            if ((mask & 0b0111100000) == 0) cnt++;
            if (cnt == 0 && (mask & 0b0001111000) == 0) cnt++;
            ans += cnt;
        }
        return ans;
    }
};

Go

func maxNumberOfFamilies(n int, reservedSeats [][]int) int {
    row := map[int]int{}
    for _, r := range reservedSeats {
        row[r[0]] |= 1 << (r[1] - 1)
    }
    ans := (n - len(row)) * 2
    for _, mask := range row {
        cnt := 0
        if mask&0b0000011110 == 0 {
            cnt++
        }
        if mask&0b0111100000 == 0 {
            cnt++
        }
        if cnt == 0 && mask&0b0001111000 == 0 {
            cnt++
        }
        ans += cnt
    }
    return ans
}

Java

class Solution {
    public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
        Map<Integer, Integer> row = new HashMap<>();
        for (int[] r : reservedSeats)
            row.put(r[0], row.getOrDefault(r[0], 0) | (1 << (r[1] - 1)));
        int ans = (n - row.size()) * 2;
        for (int mask : row.values()) {
            int cnt = 0;
            if ((mask & 0b0000011110) == 0) cnt++;
            if ((mask & 0b0111100000) == 0) cnt++;
            if (cnt == 0 && (mask & 0b0001111000) == 0) cnt++;
            ans += cnt;
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun maxNumberOfFamilies(n: Int, reservedSeats: Array<IntArray>): Int {
        val row = mutableMapOf<Int, Int>()
        for (r in reservedSeats)
            row[r[0]] = row.getOrDefault(r[0], 0) or (1 shl (r[1] - 1))
        var ans = (n - row.size) * 2
        for (mask in row.values) {
            var cnt = 0
            if (mask and 0b0000011110 == 0) cnt++
            if (mask and 0b0111100000 == 0) cnt++
            if (cnt == 0 && mask and 0b0001111000 == 0) cnt++
            ans += cnt
        }
        return ans
    }
}

Python

class Solution:
    def maxNumberOfFamilies(self, n: int, reservedSeats: list[list[int]]) -> int:
        row = {}
        for r, c in reservedSeats:
            row[r] = row.get(r, 0) | (1 << (c - 1))
        ans = (n - len(row)) * 2
        for mask in row.values():
            cnt = 0
            if mask & 0b0000011110 == 0:
                cnt += 1
            if mask & 0b0111100000 == 0:
                cnt += 1
            if cnt == 0 and mask & 0b0001111000 == 0:
                cnt += 1
            ans += cnt
        return ans

Rust

use std::collections::HashMap;
impl Solution {
    pub fn max_number_of_families(n: i32, reserved_seats: Vec<Vec<i32>>) -> i32 {
        let mut row = HashMap::new();
        for r in reserved_seats {
            row.entry(r[0]).and_modify(|e| *e |= 1 << (r[1] - 1)).or_insert(1 << (r[1] - 1));
        }
        let mut ans = (n - row.len() as i32) * 2;
        for &mask in row.values() {
            let mut cnt = 0;
            if mask & 0b0000011110 == 0 { cnt += 1; }
            if mask & 0b0111100000 == 0 { cnt += 1; }
            if cnt == 0 && mask & 0b0001111000 == 0 { cnt += 1; }
            ans += cnt;
        }
        ans
    }
}

TypeScript

class Solution {
    maxNumberOfFamilies(n: number, reservedSeats: number[][]): number {
        const row = new Map<number, number>();
        for (const [r, c] of reservedSeats)
            row.set(r, (row.get(r) ?? 0) | (1 << (c - 1)));
        let ans = (n - row.size) * 2;
        for (const mask of row.values()) {
            let cnt = 0;
            if ((mask & 0b0000011110) === 0) cnt++;
            if ((mask & 0b0111100000) === 0) cnt++;
            if (cnt === 0 && (mask & 0b0001111000) === 0) cnt++;
            ans += cnt;
        }
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(m), where m is the number of reserved seats.
• 🧺 Space complexity: O(m), for the map of reserved rows.