Circular Array Loop

Problem

You are playing a game involving a circular array of non-zero integers nums. Each nums[i] denotes the number of indices forward/backward you must move if you are located at index i:

• If nums[i] is positive, move nums[i] steps forward, and
• If nums[i] is negative, move nums[i] steps backward.

Since the array is circular, you may assume that moving forward from the last element puts you on the first element, and moving backwards from the first element puts you on the last element.

A cycle in the array consists of a sequence of indices seq of length k where:

• Following the movement rules above results in the repeating index sequence seq[0] -> seq[1] -> ... -> seq[k - 1] -> seq[0] -> ...
• Every nums[seq[j]] is either all positive or all negative.
• k > 1

Return true if there is a cycle in nums, or false otherwise.

Examples

Example 1:

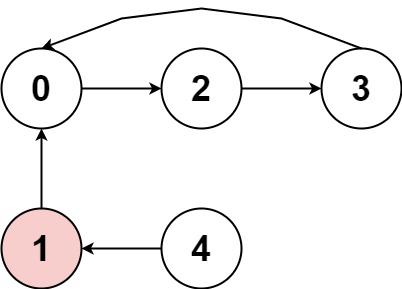
Input:
nums = [2,-1,1,2,2]
Output:
 true
Explanation: The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 2 --> 3 --> 0 --> ..., and all of its nodes are white (jumping in the same direction).

Example 2:

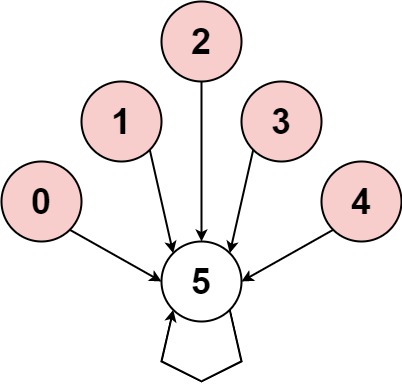
Input:
nums = [-1,-2,-3,-4,-5,6]
Output:
 false
Explanation: The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
The only cycle is of size 1, so we return false.

Example 3:

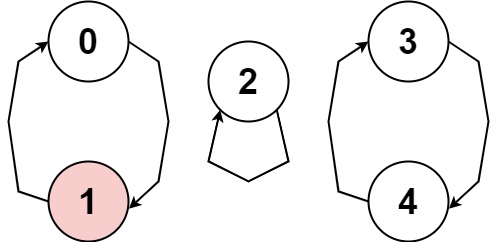
Input:
nums = [1,-1,5,1,4]
Output:
 true
Explanation: The graph shows how the indices are connected. White nodes are jumping forward, while red is jumping backward.
We can see the cycle 0 --> 1 --> 0 --> ..., and while it is of size > 1, it has a node jumping forward and a node jumping backward, so **it is not a cycle**.
We can see the cycle 3 --> 4 --> 3 --> ..., and all of its nodes are white (jumping in the same direction).

Solution

Method 1 – Two Pointers (Floyd's Cycle Detection)

Intuition

We want to detect a cycle in a circular array where all elements in the cycle move in the same direction (all positive or all negative) and the cycle length is greater than 1. We use the two pointers (Floyd's Tortoise and Hare) technique to detect cycles efficiently. To avoid revisiting the same paths, we mark visited elements as 0.

Approach

1. For each index i, if nums[i] is 0, skip (already visited).
2. Use two pointers, slow and fast, starting at i and next(i) respectively.
3. Move slow by one step and fast by two steps, always checking that the direction is the same (all positive or all negative).
4. If slow meets fast:
   • If the cycle length is more than 1 (i.e., slow != next(slow)), return True.
   • Otherwise, break.
5. After checking, mark all nodes in this path as visited (set to 0) to avoid redundant work.
6. If no valid cycle is found, return False.

Code

C++

#include <vector>
using namespace std;

class Solution {
public:
    bool circularArrayLoop(vector<int>& nums) {
        int n = nums.size();
        for (int i = 0; i < n; ++i) {
            if (!nums[i]) continue;
            int slow = i, fast = next(nums, i);
            while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(nums, fast)] > 0) {
                if (slow == fast) {
                    if (slow != next(nums, slow)) return true;
                    break;
                }
                slow = next(nums, slow);
                fast = next(nums, next(nums, fast));
            }
            int j = i;
            while (nums[j] * nums[next(nums, j)] > 0) {
                nums[j] = 0;
                j = next(nums, j);
            }
        }
        return false;
    }

    int next(vector<int>& nums, int i) {
        int n = nums.size();
        return (i + nums[i] % n + n) % n;
    }
};

Go

func circularArrayLoop(nums []int) bool {
    n := len(nums)
    for i := 0; i < n; i++ {
        if nums[i] == 0 {
            continue
        }
        slow, fast := i, next(nums, i)
        for nums[slow]*nums[fast] > 0 && nums[slow]*nums[next(nums, fast)] > 0 {
            if slow == fast {
                if slow != next(nums, slow) {
                    return true
                }
                break
            }
            slow = next(nums, slow)
            fast = next(nums, next(nums, fast))
        }
        j := i
        for nums[j]*nums[next(nums, j)] > 0 {
            nums[j] = 0
            j = next(nums, j)
        }
    }
    return false
}

func next(nums []int, i int) int {
    n := len(nums)
    return (i + nums[i]%n + n) % n
}

Java

class Solution {
    public boolean circularArrayLoop(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            if (nums[i] == 0) continue;
            int slow = i, fast = next(nums, i);
            while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(nums, fast)] > 0) {
                if (slow == fast) {
                    if (slow != next(nums, slow)) return true;
                    break;
                }
                slow = next(nums, slow);
                fast = next(nums, next(nums, fast));
            }
            int j = i;
            while (nums[j] * nums[next(nums, j)] > 0) {
                nums[j] = 0;
                j = next(nums, j);
            }
        }
        return false;
    }

    private int next(int[] nums, int i) {
        int n = nums.length;
        return (i + nums[i] % n + n) % n;
    }
}

Kotlin

class Solution {
    fun circularArrayLoop(nums: IntArray): Boolean {
        val n = nums.size
        fun next(i: Int): Int = (i + nums[i] % n + n) % n
        for (i in 0 until n) {
            if (nums[i] == 0) continue
            var slow = i
            var fast = next(i)
            while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(fast)] > 0) {
                if (slow == fast) {
                    if (slow != next(slow)) return true
                    break
                }
                slow = next(slow)
                fast = next(next(fast))
            }
            var j = i
            while (nums[j] * nums[next(j)] > 0) {
                nums[j] = 0
                j = next(j)
            }
        }
        return false
    }
}

Python

from typing import List

class Solution:
    def circularArrayLoop(self, nums: List[int]) -> bool:
        n = len(nums)

        def next(i):
            return (i + nums[i] % n + n) % n

        for i in range(n):
            if nums[i] == 0:
                continue
            slow, fast = i, next(i)
            while nums[slow] * nums[fast] > 0 and nums[slow] * nums[next(fast)] > 0:
                if slow == fast:
                    if slow != next(slow):
                        return True
                    break
                slow, fast = next(slow), next(next(fast))
            j = i
            while nums[j] * nums[next(j)] > 0:
                nums[j] = 0
                j = next(j)
        return False

Rust

impl Solution {
    pub fn circular_array_loop(nums: Vec<i32>) -> bool {
        let n = nums.len();
        let mut nums = nums;
        fn next(nums: &Vec<i32>, i: usize) -> usize {
            let n = nums.len();
            ((i as i32 + (nums[i] % n as i32) + n as i32) % n as i32) as usize
        }
        for i in 0..n {
            if nums[i] == 0 { continue; }
            let mut slow = i;
            let mut fast = next(&nums, i);
            while nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(&nums, fast)] > 0 {
                if slow == fast {
                    if slow != next(&nums, slow) { return true; }
                    break;
                }
                slow = next(&nums, slow);
                fast = next(&nums, next(&nums, fast));
            }
            let mut j = i;
            while nums[j] * nums[next(&nums, j)] > 0 {
                nums[j] = 0;
                j = next(&nums, j);
            }
        }
        false
    }
}

TypeScript

function circularArrayLoop(nums: number[]): boolean {
    const n = nums.length;
    const next = (i: number) => (i + ((nums[i] % n) + n) % n) % n;
    for (let i = 0; i < n; i++) {
        if (nums[i] === 0) continue;
        let slow = i, fast = next(i);
        while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(fast)] > 0) {
            if (slow === fast) {
                if (slow !== next(slow)) return true;
                break;
            }
            slow = next(slow);
            fast = next(next(fast));
        }
        let j = i;
        while (nums[j] * nums[next(j)] > 0) {
            nums[j] = 0;
            j = next(j);
        }
    }
    return false;
}

Complexity

• ⏰ Time complexity: O(n), where n is the length of nums. Each element is visited at most twice (once by slow/fast, once when marking visited).
• 🧺 Space complexity: O(1), since we use only a constant amount of extra space (in-place marking).