Climbing Stairs - Take atmost 2 Steps

Problem

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

OR

There are n stairs, a person standing at the bottom wants to reach the top. The person can climb either 1 stair or 2 stairs at a time. Count the number of ways, the person can reach the top.

Examples

Example 1:

Input: n = 1
Output: 1
Explanation: There is only one way to climb 1 stair

Example 2:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 3:

Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Example 4:

Input: n = 4
Output: 5
Explanation: Here are the steps - (1, 1, 1, 1), (1, 1, 2), (2, 1, 1), (1, 2, 1), (2, 2).

Solution

Video explanation

Here is the video explaining this method in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/KGPfpZfPnD0" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Backtracking

This approach uses Depth-First Search (DFS) or backtracking to explore all possible paths to climb the staircase. At each step, the function recursively adds either 1 step or 2 steps, terminating when the step count either reaches or exceeds n.

Here si the approach:

1. Start the recursion (DFS) from step 0.
2. At each step:
   • Add 1 step to the current step and call the function recursively.
   • Add 2 steps to the current step and call the function recursively.
3. Base Cases:
   • If current_step == n, the path is valid, so return 1.
   • If current_step > n, the path exceeds the total steps, so return 0.
4. Accumulate valid paths for both choices (taking 1 step or 2 steps).

Here is how the recursion tree will look like:

graph TD;
A("0:4") ---|1 step| B(1)
A ---|2 steps| C(2)

B ---|1 step| D(2)
B ---|2 steps| E(3)

C ---|1 step| F(3)
C ---|2 steps| G(4):::green

D ---|1 step| H(3)
D ---|2 steps| I(4):::green

E ---|1 step| J(4):::green
E ---|2 steps| K(5):::red

F ---|1 step| L(4):::green
F ---|2 steps| M(5):::red

H ---|1 step| N(4):::green
H ---|2 steps| O(5):::red


classDef green fill:#3CB371,stroke:#000,stroke-width:1px,color:#fff; 
classDef red fill:#FF0000,stroke:#000,stroke-width:1px,color:#fff;

As, you can see the total number of green or valid nodes are 5.

Code

Java

class Solution {

    public int climbStairs(int n) {
        // Helper function for DFS
        return dfs(0, n);
    }

    private int dfs(int currentStep, int n) {
        // Base case 1: Valid path (reached exactly n)
        if (currentStep == n) {
            return 1;
        }
        // Base case 2: Invalid path (exceeded n)
        if (currentStep > n) {
            return 0;
        }

        // Recursive exploration: Take 1 step or take 2 steps
        return dfs(currentStep + 1, n) + dfs(currentStep + 2, n);
    }
}

Python

class Solution:
    def climbStairs(self, n: int) -> int:
        def dfs(current_step: int) -> int:
            # Base case 1: Valid path (reached exactly n)
            if current_step == n:
                return 1
            # Base case 2: Invalid path (exceeded n)
            if current_step > n:
                return 0
            
            # Recursive exploration: Take 1 step or take 2 steps
            return dfs(current_step + 1) + dfs(current_step + 2)
        
        # Start backtracking from step 0
        return dfs(0)

Complexity

• ⏰ Time complexity: O(2^n). The total number of paths is roughly 2^n because two recursive calls are made at each step.
• 🧺 Space complexity: O(n), as the recursion stack can grow up to n levels deep.

Method 2 - Recursion

We can easily find recursive nature in above problem.

Lets take n = 2, then we have 2 ways - either take 1 step twice or 2 steps in one go.

For n = 3, we have 3 ways:

• One Step at a time
• Two-step then one step
• One step then Two-step

For n = 4, we have 5 ways: (1, 1, 1, 1), (2, 2), (1, 1, 2), (2, 1, 1), (1, 2, 1)

Now, lets take n = 6, and try to get the algorithm.

So in the next step, we need to calculate the number of ways taken to raise 5 steps and 4 steps.

We can build full tree for the steps taken as below (not complete for clarity):

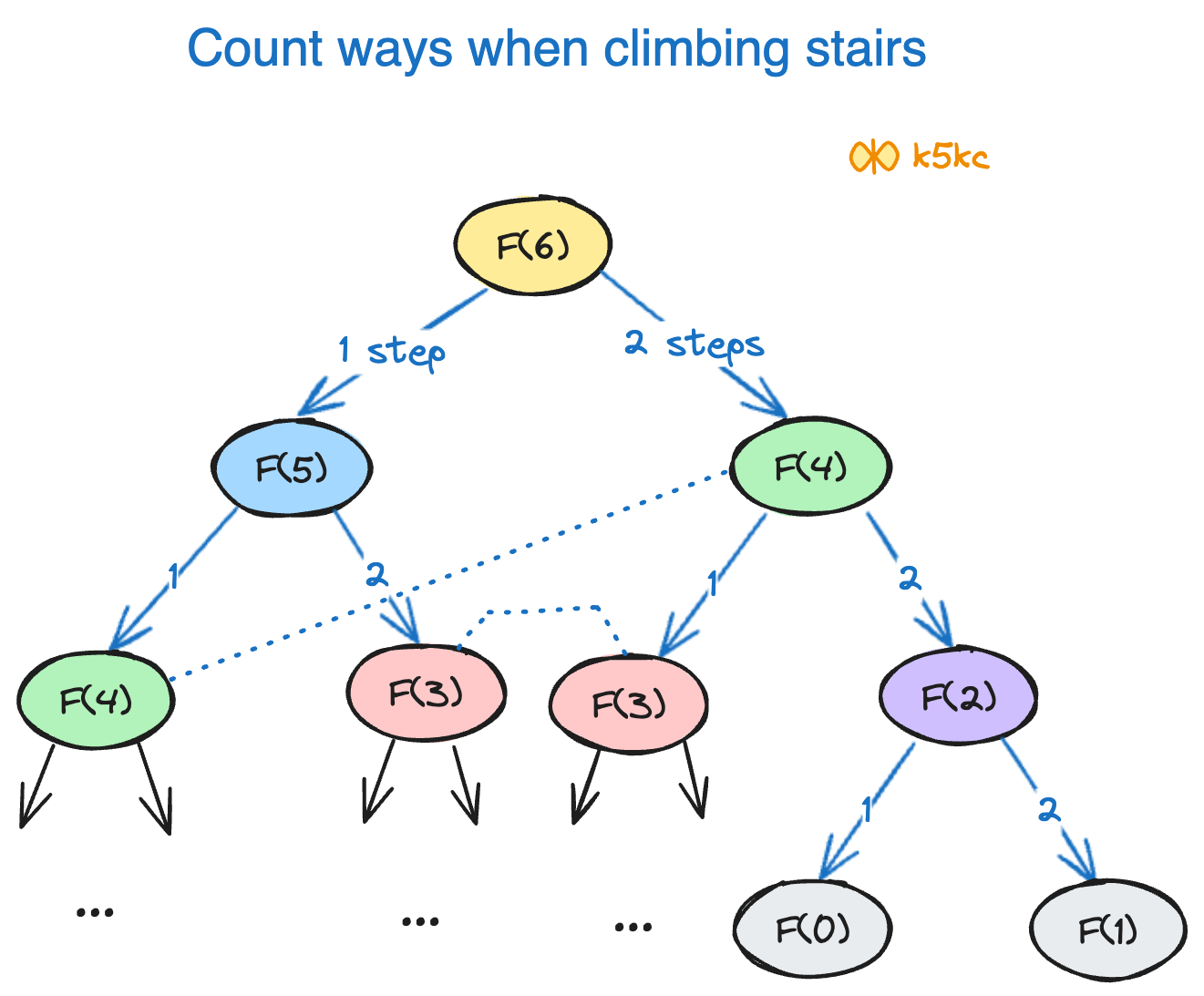
Code

Java

class Solution {
    public int climbStairs(int n) {
        // Base cases
        if (n == 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        }
        
        // Recurrence relation
        return climbStairs(n - 1) + climbStairs(n - 2);
    }
}

Python

class Solution:
    def climbStairs(self, n: int) -> int:
        # Base cases
        if n == 1:
            return 1
        elif n == 2:
            return 2
        
        # Recurrence relation
        return self.climbStairs(n - 1) + self.climbStairs(n - 2)

Complexity

• ⏰ Time complexity: O(2^n), because overlapping subproblems are recomputed multiple times.
• 🧺 Space complexity: O(n) due to recursion stack.

Method 3 - Top Down DP

The naive recursive approach recalculates overlapping subproblems multiple times, leading to inefficiency. By using a memoisation table (cache), you can store results of previously computed subproblems to avoid redundant calculations.

Here is the approach:

• Use a cache (HashMap or dictionary) to store results for each step:
  • If the result for n is already computed, retrieve it from the cache.
  • Otherwise, compute ways(n) recursively: ways(n) = ways(n-1) + ways(n-2)
  • Save the result for n in the cache for future use.

Code

Java

class Solution {

    // Create a cache (HashMap) to store results for previously computed steps
    private HashMap<Integer, Integer> memo = new HashMap<>();

    public int climbStairs(int n) {
        // Base cases
        if (n == 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        }

        // Use cached value if it's already computed
        if (memo.containsKey(n)) {
            return memo.get(n);
        }

        // Recurrence relation: Combine results for (n-1) and (n-2)
        int result = climbStairs(n - 1) + climbStairs(n - 2);

        // Cache the result
        memo.put(n, result);
        return result;
    }
}

Python

class Solution:
    def climbStairs(self, n: int) -> int:
        # Create a cache (dictionary) to store results for previously computed steps
        memo = {}

        def dp(current: int) -> int:
            # Base cases
            if current == 1:
                return 1
            elif current == 2:
                return 2
            
            # Use cached value if it's already computed
            if current in memo:
                return memo[current]
            
            # Recurrence relation: Combine results for (n-1) and (n-2)
            memo[current] = dp(current - 1) + dp(current - 2)
            return memo[current]
        
        # Start the recursive top-down approach from step n
        return dp(n)

Complexity

• ⏰ Time complexity: O(n)
• 🧺 Space complexity: O(n)

Method 4 - Bottom Up DP

Instead of recursion, build the solution iteratively using a dp table. Once base cases are solved (dp[1] = 1, dp[2] = 2), compute the number of ways for each step up to n by combining results for the previous two steps. This avoids recursion overhead and ensures every subproblem is solved sequentially.

Here is the approach:

• Initialise a dp array of size n+1 (to store results for steps 1 to n).
• Populate the base cases:
  • dp[1] = 1
  • dp[2] = 2.
• Use the recurrence relation iteratively: dp[i] = dp[i-1] + dp[i-2]
• Return the value stored at dp[n].

Code

Java

 class Solution {
     public int climbStairs(int n) {
         // If the staircase has only 1 or 2 steps, return n directly
         if (n == 1) {
             return 1;
         } else if (n == 2) {
             return 2;
         }
 
         // Create a DP table to store the number of ways for each step
         int[] dp = new int[n + 1];
 
         // Base cases
         dp[1] = 1;
         dp[2] = 2;
 
         // Fill the DP table using the relation dp[i] = dp[i-1] + dp[i-2]
         for (int i = 3; i <= n; i++) {
             dp[i] = dp[i - 1] + dp[i - 2];
         }
 
         // The final answer is the number of ways to reach step n
         return dp[n];
     }
 }

Python

class Solution:
    def climbStairs(self, n: int) -> int:
        # If the staircase has only 1 or 2 steps, return n directly
        if n == 1:
            return 1
        elif n == 2:
            return 2

        # Create a DP table to store the number of ways for each step
        dp = [0] * (n + 1)

        # Base cases
        dp[1] = 1
        dp[2] = 2

        # Fill the DP table using the relation dp[i] = dp[i-1] + dp[i-2]
        for i in range(3, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]

        # The final answer is the number of ways to reach step n
        return dp[n]

Complexity

• ⏰ Time complexity: O(n)
• 🧺 Space complexity: O(n) for using the dp tale

Method 5 - Space efficient Bottom up DP

While the bottom-up DP uses a dp table, observe that only the last two values, dp[i-1] and dp[i-2], are needed to compute dp[i]. This allows us to optimise space by storing only two variables (prev1 and prev2) instead of maintaining an entire table.

Here is the approach:

• Initialise two variables:
  • prev1 holds dp[i-1] (starting with dp[2] = 2).
  • prev2 holds dp[i-2] (starting with dp[1] = 1).
• Iteratively compute the current value using the relation: curr = prev1 + prev2
• Shift the variables:
  • prev2 = prev1
  • prev1 = curr.
• Return the final value (prev1).

Code

Java

class Solution {

    public int climbStairs(int n) {
        // Base cases for small values of n
        if (n == 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        }

        // Initialise variables representing dp[i-2] and dp[i-1]
        int prev2 = 1; // dp[1]
        int prev1 = 2; // dp[2]

        // Iterate from step 3 to step n
        for (int i = 3; i <= n; i++) {
            int current = prev1 + prev2; // Compute dp[i] = dp[i-1] + dp[i-2]
            prev2 = prev1; // Update dp[i-2] to dp[i-1]
            prev1 = current; // Update dp[i-1] to dp[i]
        }

        return prev1; // dp[n] is stored in prev1 at the end
    }
}

Python

class Solution:
    def climbStairs(self, n: int) -> int:
        # Base cases for small values of n
        if n == 1:
            return 1
        elif n == 2:
            return 2

        # Initialise the variables representing dp[i-2] and dp[i-1]
        prev2 = 1  # dp[1]
        prev1 = 2  # dp[2]

        # Iterate from step 3 to step n
        for i in range(3, n + 1):
            current = prev1 + prev2  # Compute dp[i] = dp[i-1] + dp[i-2]
            prev2 = prev1  # Update dp[i-2] to dp[i-1]
            prev1 = current  # Update dp[i-1] to dp[i]

        return prev1  # dp[n] is stored in prev1 at the end

Complexity

• ⏰ Time complexity: O(n). We iterate through all steps from 3 to n.
• 🧺 Space complexity: O(1). Uses only two variables (prev1 and prev2), avoiding the need for a DP table.

Method 6- Using Fibonacci Numbers

The number of ways to reach the n-th stair on a staircase depends on whether you can take one step at a time (from the (n-1)th stair) or two steps at a time (from the (n-2)th stair). We'll represent this total number of ways to reach the n-th stair as ways(n).

ways(n) = ways(n-1) + ways(n-2)

This is actually formula for [generating nth fibonacci number](generate-nth-fibonacci-number). But notice one thing that ways(n) is equal to fib(n+1), hence we can reuse fib(n) function.

ways(1) = fib(2) = 1
ways(2) = fib(3) = 2
ways(3) = fib(4) = 3

Code

Java

// Returns number of ways to reach s'th stair
public int climbStairs(int s) {
	return fib(s + 1);
}

Complexity

• ⏰ Time complexity: O(n). (It can be optimized to work in O(Logn) time using matrix approach)
• 🧺 Space complexity: O(n)