Clone Binary Tree With Random Pointer

Problem

A binary tree is given such that each node contains an additional random pointer which could point to any node in the tree or null.

Return a deep copy of the tree.

The tree is represented in the same input/output way as normal binary trees where each node is represented as a pair of [val, random_index] where:

val: an integer representing Node.val
random_index: the index of the node (in the input) where the random pointer points to, or null if it does not point to any node.

You will be given the tree in class Node and you should return the cloned tree in class NodeCopy. NodeCopy class is just a clone of Node class with the same attributes and constructors.

Examples

Example 1:

1
2
3
4
5
6
7


![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1400-1499/1485.Clone%20Binary%20Tree%20With%20Random%20Pointer/images/clone_1.png)
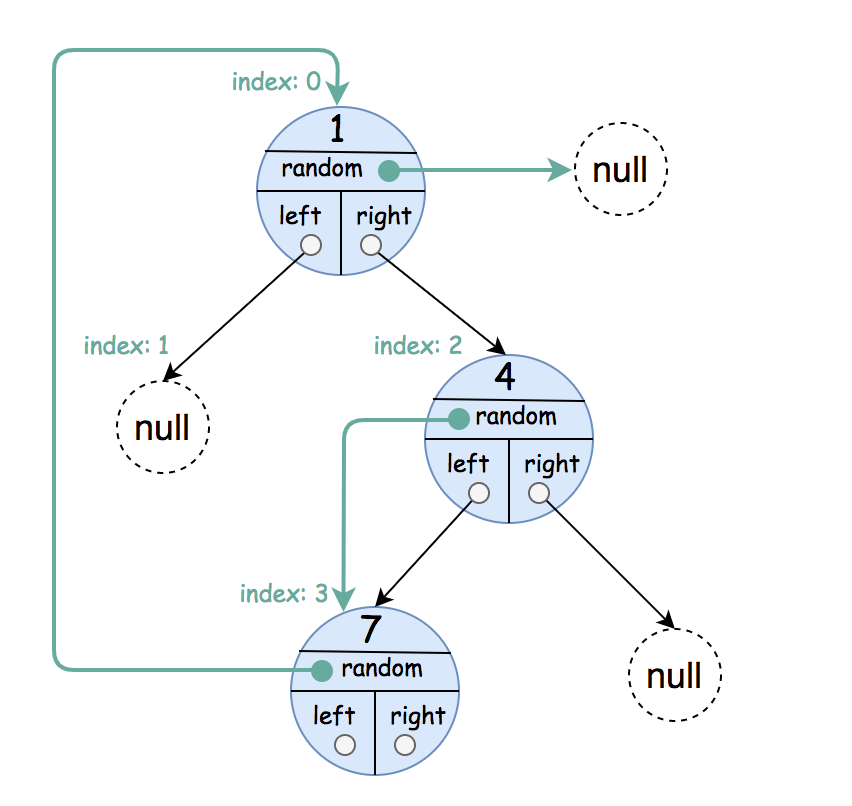
    Input: root = [[1,null],null,[4,3],[7,0]]
    Output: [[1,null],null,[4,3],[7,0]]
    Explanation: The original binary tree is [1,null,4,7].
    The random pointer of node one is null, so it is represented as [1, null].
    The random pointer of node 4 is node 7, so it is represented as [4, 3] where 3 is the index of node 7 in the array representing the tree.
    The random pointer of node 7 is node 1, so it is represented as [7, 0] where 0 is the index of node 1 in the array representing the tree.

Example 2:

1
2
3
4


![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1400-1499/1485.Clone%20Binary%20Tree%20With%20Random%20Pointer/images/clone_2.png)
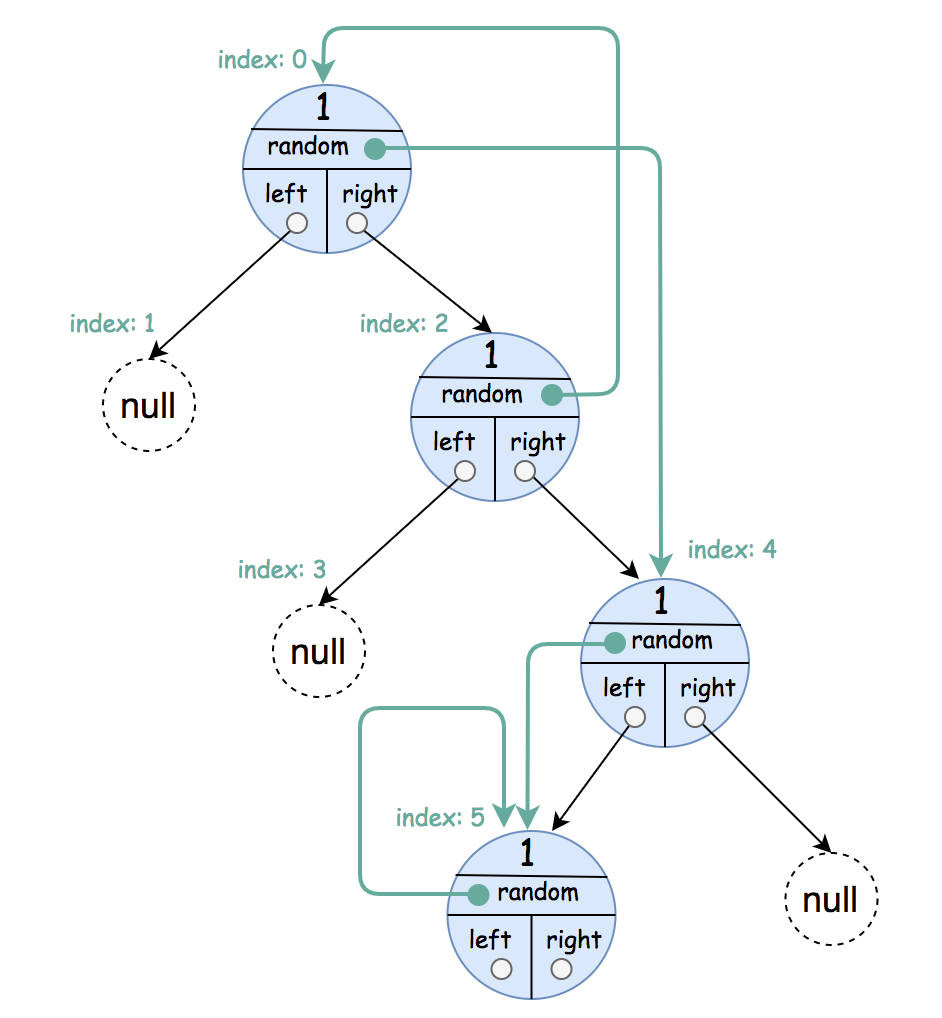
    Input: root = [[1,4],null,[1,0],null,[1,5],[1,5]]
    Output: [[1,4],null,[1,0],null,[1,5],[1,5]]
    Explanation: The random pointer of a node can be the node itself.

Example 3:

1
2
3


![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1400-1499/1485.Clone%20Binary%20Tree%20With%20Random%20Pointer/images/clone_3.png)
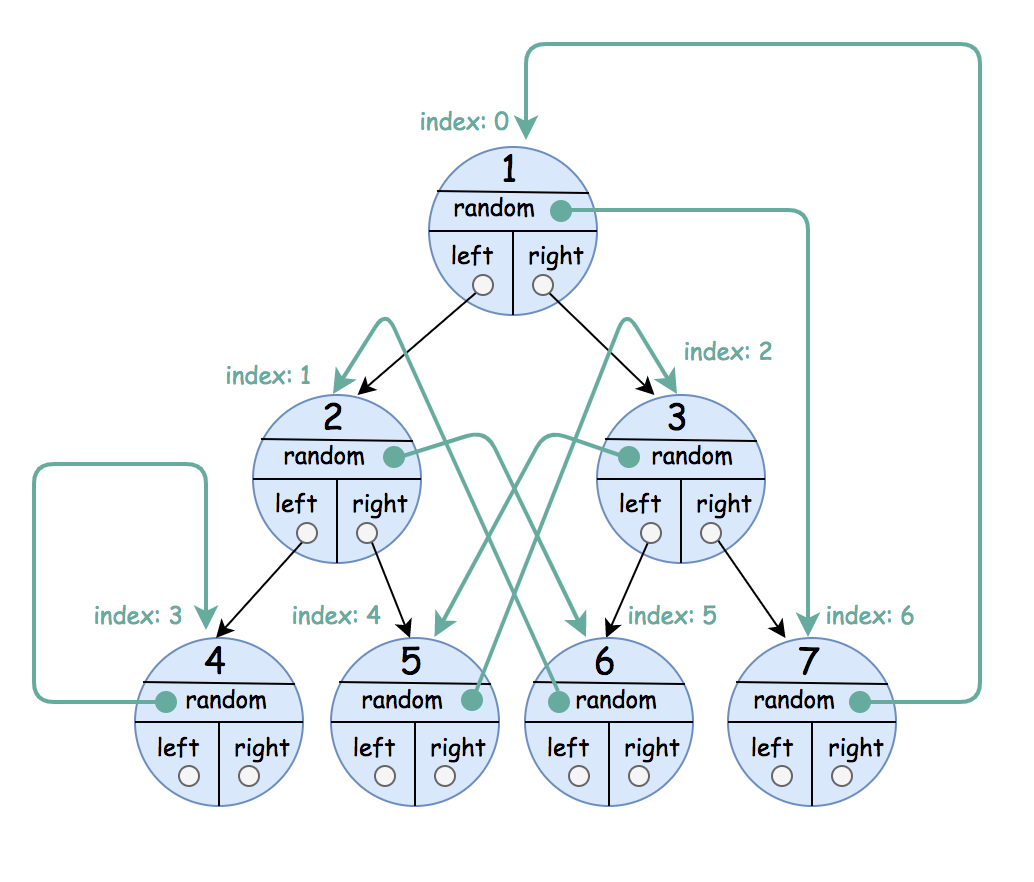
    Input: root = [[1,6],[2,5],[3,4],[4,3],[5,2],[6,1],[7,0]]
    Output: [[1,6],[2,5],[3,4],[4,3],[5,2],[6,1],[7,0]]

Constraints:

The number of nodes in the tree is in the range [0, 1000].
1 <= Node.val <= 10^6

Solution

Method 1 – Hash Map (DFS or BFS)

Intuition

To clone a binary tree with random pointers, we need to create a copy of each node and ensure that the left, right, and random pointers in the new tree point to the corresponding cloned nodes. We use a hash map to map original nodes to their clones, so we can set the random pointers correctly.

Approach

Traverse the original tree (DFS or BFS).
For each node, create a clone and store the mapping from the original node to the clone in a hash map.
Recursively (or iteratively) set the left, right, and random pointers for each clone using the hash map.
Return the clone of the root node.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
public:
    unordered_map<Node*, NodeCopy*> mp;
    NodeCopy* copyRandomBinaryTree(Node* root) {
        if (!root) return nullptr;
        if (mp.count(root)) return mp[root];
        NodeCopy* node = new NodeCopy(root->val);
        mp[root] = node;
        node->left = copyRandomBinaryTree(root->left);
        node->right = copyRandomBinaryTree(root->right);
        node->random = copyRandomBinaryTree(root->random);
        return node;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


type Node struct {
    Val int
    Left, Right, Random *Node
}
type NodeCopy struct {
    Val int
    Left, Right, Random *NodeCopy
}
func copyRandomBinaryTree(root *Node) *NodeCopy {
    mp := map[*Node]*NodeCopy{}
    var dfs func(*Node) *NodeCopy
    dfs = func(n *Node) *NodeCopy {
        if n == nil { return nil }
        if v, ok := mp[n]; ok { return v }
        node := &NodeCopy{Val: n.Val}
        mp[n] = node
        node.Left = dfs(n.Left)
        node.Right = dfs(n.Right)
        node.Random = dfs(n.Random)
        return node
    }
    return dfs(root)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    Map<Node, NodeCopy> mp = new HashMap<>();
    public NodeCopy copyRandomBinaryTree(Node root) {
        if (root == null) return null;
        if (mp.containsKey(root)) return mp.get(root);
        NodeCopy node = new NodeCopy(root.val);
        mp.put(root, node);
        node.left = copyRandomBinaryTree(root.left);
        node.right = copyRandomBinaryTree(root.right);
        node.random = copyRandomBinaryTree(root.random);
        return node;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    private val mp = mutableMapOf<Node, NodeCopy>()
    fun copyRandomBinaryTree(root: Node?): NodeCopy? {
        if (root == null) return null
        if (mp.containsKey(root)) return mp[root]
        val node = NodeCopy(root.`val`)
        mp[root] = node
        node.left = copyRandomBinaryTree(root.left)
        node.right = copyRandomBinaryTree(root.right)
        node.random = copyRandomBinaryTree(root.random)
        return node
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution:
    def copyRandomBinaryTree(self, root: 'Node') -> 'NodeCopy':
        mp = {}
        def dfs(node):
            if not node:
                return None
            if node in mp:
                return mp[node]
            node_copy = NodeCopy(node.val)
            mp[node] = node_copy
            node_copy.left = dfs(node.left)
            node_copy.right = dfs(node.right)
            node_copy.random = dfs(node.random)
            return node_copy
        return dfs(root)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


use std::collections::HashMap;
impl Solution {
    pub fn copy_random_binary_tree(root: Option<Rc<RefCell<Node>>>) -> Option<Rc<RefCell<NodeCopy>>> {
        fn dfs(
            node: Option<Rc<RefCell<Node>>>,
            mp: &mut HashMap<*const Node, Rc<RefCell<NodeCopy>>>,
        ) -> Option<Rc<RefCell<NodeCopy>>> {
            if let Some(n) = node {
                let ptr = Rc::as_ptr(&n);
                if let Some(c) = mp.get(&ptr) {
                    return Some(Rc::clone(c));
                }
                let node_copy = Rc::new(RefCell::new(NodeCopy::new(n.borrow().val)));
                mp.insert(ptr, Rc::clone(&node_copy));
                node_copy.borrow_mut().left = dfs(n.borrow().left.clone(), mp);
                node_copy.borrow_mut().right = dfs(n.borrow().right.clone(), mp);
                node_copy.borrow_mut().random = dfs(n.borrow().random.clone(), mp);
                Some(node_copy)
            } else {
                None
            }
        }
        let mut mp = HashMap::new();
        dfs(root, &mut mp)
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


class Solution {
    copyRandomBinaryTree(root: Node | null): NodeCopy | null {
        const mp = new Map<Node, NodeCopy>();
        function dfs(node: Node | null): NodeCopy | null {
            if (!node) return null;
            if (mp.has(node)) return mp.get(node)!;
            const nodeCopy = new NodeCopy(node.val);
            mp.set(node, nodeCopy);
            nodeCopy.left = dfs(node.left);
            nodeCopy.right = dfs(node.right);
            nodeCopy.random = dfs(node.random);
            return nodeCopy;
        }
        return dfs(root);
    }
}

Complexity

⏰ Time complexity: O(n), where n is the number of nodes.
🧺 Space complexity: O(n), for the hash map and recursion stack.

Problem#

Examples#

Solution#

Method 1 – Hash Map (DFS or BFS)#

Intuition#

Approach#

Code#

Complexity#