Clone N-ary Tree
MediumUpdated: Jul 7, 2025
Practice on:
Problem
Given a root of an N-ary tree, return a deep copy (clone) of the tree.
Each node in the n-ary tree contains a val (int) and a list (List[Node]) of its children.
class Node { public int val; public List<Node> children; }
Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).
Examples
Example 1:
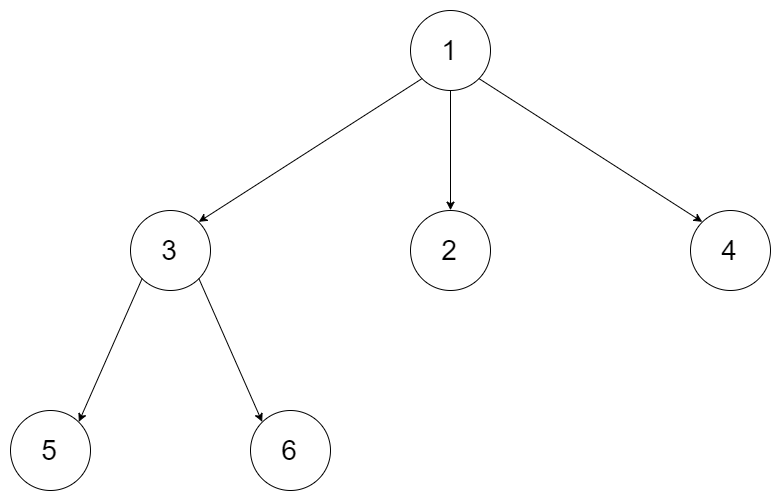
Input: root = [1,null,3,2,4,null,5,6]
Output: [1,null,3,2,4,null,5,6]
Example 2:
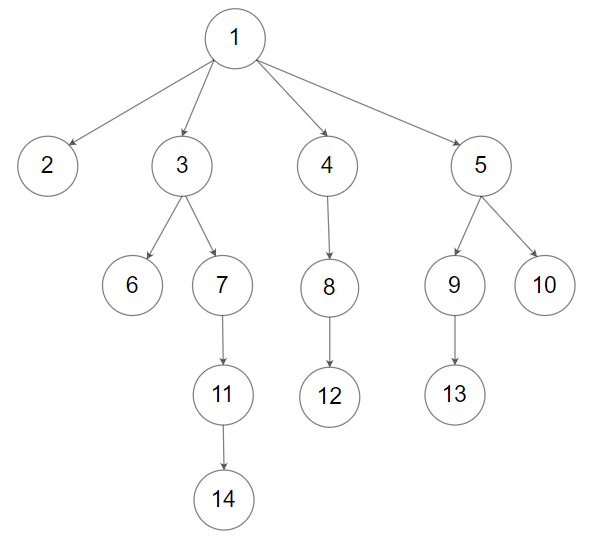
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Constraints:
- The depth of the n-ary tree is less than or equal to
1000. - The total number of nodes is between
[0, 10^4].
Follow up: Can your solution work for the [Clone Graph Problem](clone-undirected-graph)?
Solution
Method 1 – Hash Map with DFS (Recursive Cloning)
Intuition
To clone an N-ary tree, we need to create a new node for each original node and recursively clone all its children. To avoid duplicating nodes in case of cycles (though N-ary trees don't have cycles, but for generality), we use a hash map to keep track of already cloned nodes.
Approach
- Use a hash map to map original nodes to their clones.
- For each node, if it is already cloned, return the clone.
- Otherwise, create a new node with the same value.
- Recursively clone all children and add them to the new node's children list.
- Return the cloned node.
Code
C++
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) : val(_val) {}
Node(int _val, vector<Node*> _children) : val(_val), children(_children) {}
};
class Solution {
public:
Node* cloneTree(Node* root) {
if (!root) return nullptr;
unordered_map<Node*, Node*> mp;
return dfs(root, mp);
}
Node* dfs(Node* node, unordered_map<Node*, Node*>& mp) {
if (!node) return nullptr;
if (mp.count(node)) return mp[node];
Node* clone = new Node(node->val);
mp[node] = clone;
for (auto child : node->children) {
clone->children.push_back(dfs(child, mp));
}
return clone;
}
};
Go
type Node struct {
Val int
Children []*Node
}
func CloneTree(root *Node) *Node {
mp := map[*Node]*Node{}
var dfs func(*Node) *Node
dfs = func(node *Node) *Node {
if node == nil { return nil }
if v, ok := mp[node]; ok { return v }
clone := &Node{Val: node.Val}
mp[node] = clone
for _, child := range node.Children {
clone.Children = append(clone.Children, dfs(child))
}
return clone
}
return dfs(root)
}
Java
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int val) { this.val = val; }
public Node(int val, List<Node> children) { this.val = val; this.children = children; }
}
class Solution {
public Node cloneTree(Node root) {
Map<Node, Node> mp = new HashMap<>();
return dfs(root, mp);
}
private Node dfs(Node node, Map<Node, Node> mp) {
if (node == null) return null;
if (mp.containsKey(node)) return mp.get(node);
Node clone = new Node(node.val);
mp.put(node, clone);
if (node.children != null) {
clone.children = new ArrayList<>();
for (Node child : node.children) {
clone.children.add(dfs(child, mp));
}
}
return clone;
}
}
Kotlin
class Node(var `val`: Int) {
var children: MutableList<Node?> = mutableListOf()
}
class Solution {
fun cloneTree(root: Node?): Node? {
val mp = mutableMapOf<Node, Node>()
fun dfs(node: Node?): Node? {
if (node == null) return null
if (mp.containsKey(node)) return mp[node]
val clone = Node(node.`val`)
mp[node] = clone
for (child in node.children) {
clone.children.add(dfs(child))
}
return clone
}
return dfs(root)
}
}
Python
class Node:
def __init__(self, val: int, children: list['Node'] = None):
self.val = val
self.children = children if children is not None else []
class Solution:
def cloneTree(self, root: 'Node | None') -> 'Node | None':
mp = {}
def dfs(node: 'Node | None') -> 'Node | None':
if node is None:
return None
if node in mp:
return mp[node]
clone = Node(node.val)
mp[node] = clone
for child in node.children:
clone.children.append(dfs(child))
return clone
return dfs(root)
Rust
use std::rc::Rc;
use std::cell::RefCell;
use std::collections::HashMap;
#[derive(Debug, PartialEq, Eq)]
pub struct Node {
pub val: i32,
pub children: Vec<Rc<RefCell<Node>>>,
}
impl Node {
pub fn new(val: i32) -> Self {
Node { val, children: vec![] }
}
}
impl Solution {
pub fn clone_tree(root: Option<Rc<RefCell<Node>>>) -> Option<Rc<RefCell<Node>>> {
fn dfs(node: Option<Rc<RefCell<Node>>>, mp: &mut HashMap<usize, Rc<RefCell<Node>>>) -> Option<Rc<RefCell<Node>>> {
if let Some(n) = node {
let key = Rc::as_ptr(&n) as usize;
if let Some(clone) = mp.get(&key) { return Some(clone.clone()); }
let new_node = Rc::new(RefCell::new(Node::new(n.borrow().val)));
mp.insert(key, new_node.clone());
for child in &n.borrow().children {
new_node.borrow_mut().children.push(dfs(Some(child.clone()), mp).unwrap());
}
Some(new_node)
} else {
None
}
}
dfs(root, &mut HashMap::new())
}
}
TypeScript
class Node {
val: number;
children: Node[];
constructor(val?: number, children?: Node[]) {
this.val = val ?? 0;
this.children = children ?? [];
}
}
class Solution {
cloneTree(root: Node | null): Node | null {
const mp = new Map<Node, Node>();
function dfs(node: Node | null): Node | null {
if (!node) return null;
if (mp.has(node)) return mp.get(node)!;
const clone = new Node(node.val);
mp.set(node, clone);
for (const child of node.children) {
clone.children.push(dfs(child)!);
}
return clone;
}
return dfs(root);
}
}
Complexity
- ⏰ Time complexity:
O(N), where N is the number of nodes in the tree. Each node is visited once. - 🧺 Space complexity:
O(N), for the hash map and recursion stack.